Minimax Estimation of Distances on a Surface and Minimax Manifold Learning in the Isometric-to-Convex Setting

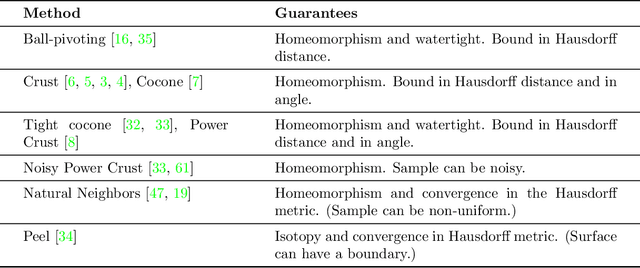
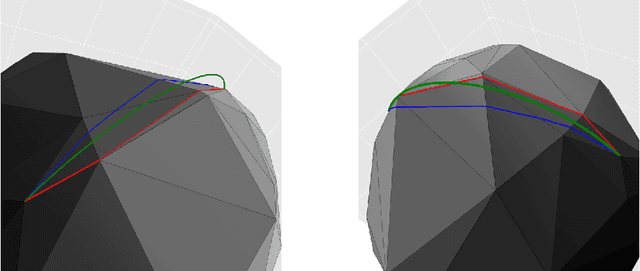
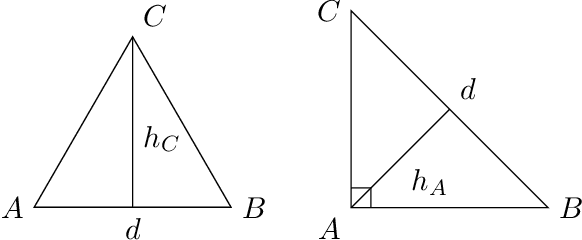
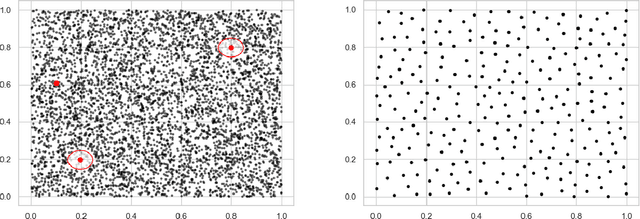
We start by considering the problem of estimating intrinsic distances on a smooth surface. We show that sharper estimates can be obtained via a reconstruction of the surface, and discuss the use of the tangential Delaunay complex for that purpose. We further show that the resulting approximation rate is in fact optimal in an information-theoretic (minimax) sense. We then turn to manifold learning and argue that a variant of Isomap where the distances are instead computed on a reconstructed surface is minimax optimal for the problem of isometric manifold embedding.