Supervising Embedding Algorithms Using the Stress

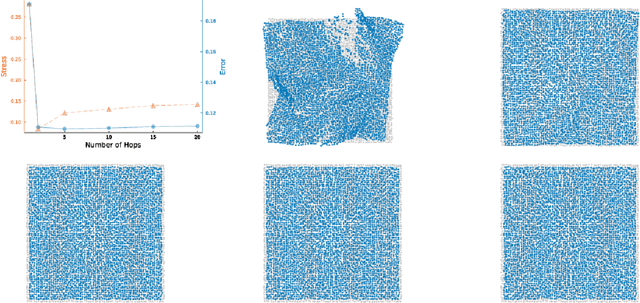
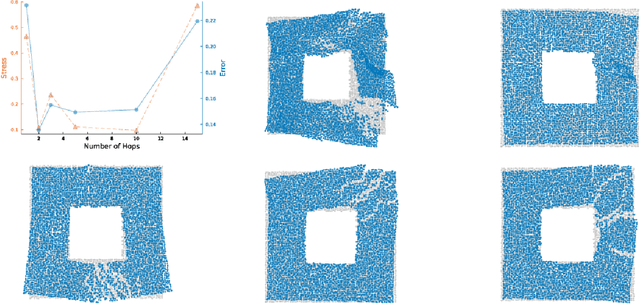
While classical scaling, just like principal component analysis, is parameter-free, most other methods for embedding multivariate data require the selection of one or several parameters. This tuning can be difficult due to the unsupervised nature of the situation. We propose a simple, almost obvious, approach to supervise the choice of tuning parameter(s): minimize a notion of stress. We substantiate this choice by reference to rigidity theory. We extend a result by Aspnes et al. (IEEE Mobile Computing, 2006), showing that general random geometric graphs are trilateration graphs with high probability. And we provide a stability result \`a la Anderson et al. (SIAM Discrete Mathematics, 2010). We illustrate this approach in the context of the MDS-MAP(P) algorithm of Shang and Ruml (IEEE INFOCOM, 2004). As a prototypical patch-stitching method, it requires the choice of patch size, and we use the stress to make that choice data-driven. In this context, we perform a number of experiments to illustrate the validity of using the stress as the basis for tuning parameter selection. In so doing, we uncover a bias-variance tradeoff, which is a phenomenon which may have been overlooked in the multidimensional scaling literature. By turning MDS-MAP(P) into a method for manifold learning, we obtain a local version of Isomap for which the minimization of the stress may also be used for parameter tuning.

Minimax Estimation of Distances on a Surface and Minimax Manifold Learning in the Isometric-to-Convex Setting

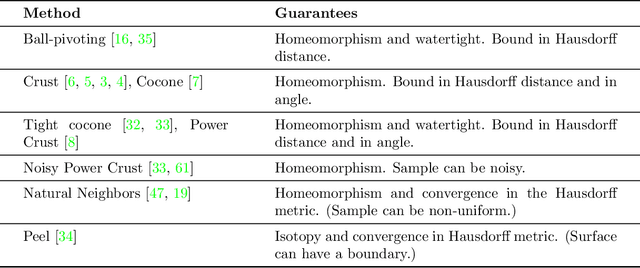
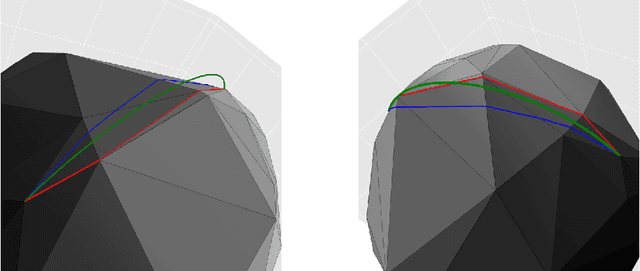
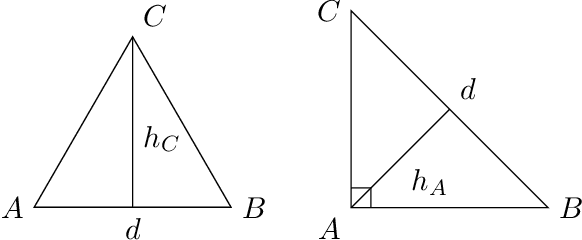
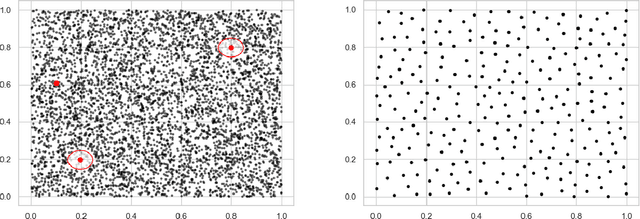
We start by considering the problem of estimating intrinsic distances on a smooth surface. We show that sharper estimates can be obtained via a reconstruction of the surface, and discuss the use of the tangential Delaunay complex for that purpose. We further show that the resulting approximation rate is in fact optimal in an information-theoretic (minimax) sense. We then turn to manifold learning and argue that a variant of Isomap where the distances are instead computed on a reconstructed surface is minimax optimal for the problem of isometric manifold embedding.