Robust Topological Inference in the Presence of Outliers

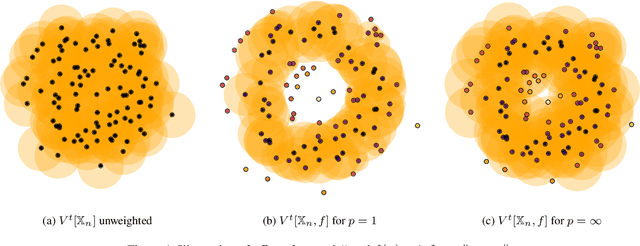
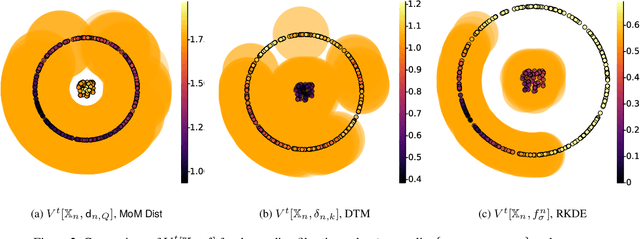
The distance function to a compact set plays a crucial role in the paradigm of topological data analysis. In particular, the sublevel sets of the distance function are used in the computation of persistent homology -- a backbone of the topological data analysis pipeline. Despite its stability to perturbations in the Hausdorff distance, persistent homology is highly sensitive to outliers. In this work, we develop a framework of statistical inference for persistent homology in the presence of outliers. Drawing inspiration from recent developments in robust statistics, we propose a $\textit{median-of-means}$ variant of the distance function ($\textsf{MoM Dist}$), and establish its statistical properties. In particular, we show that, even in the presence of outliers, the sublevel filtrations and weighted filtrations induced by $\textsf{MoM Dist}$ are both consistent estimators of the true underlying population counterpart, and their rates of convergence in the bottleneck metric are controlled by the fraction of outliers in the data. Finally, we demonstrate the advantages of the proposed methodology through simulations and applications.

Robust Persistence Diagrams using Reproducing Kernels

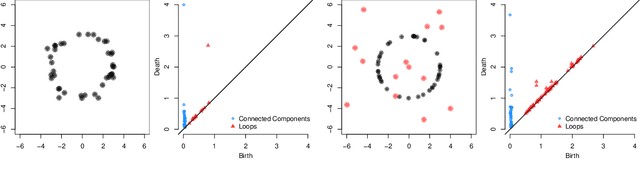
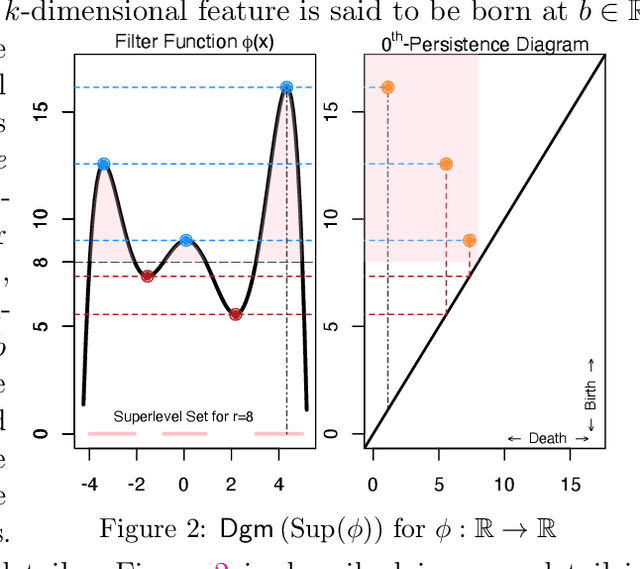
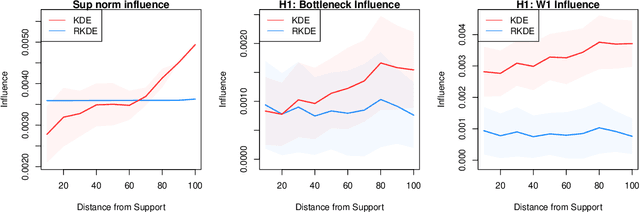
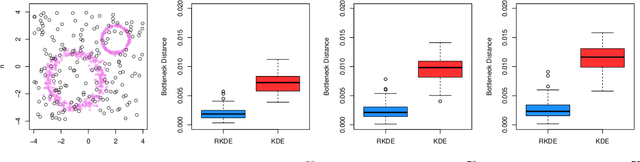
Persistent homology has become an important tool for extracting geometric and topological features from data, whose multi-scale features are summarized in a persistence diagram. From a statistical perspective, however, persistence diagrams are very sensitive to perturbations in the input space. In this work, we develop a framework for constructing robust persistence diagrams from superlevel filtrations of robust density estimators constructed using reproducing kernels. Using an analogue of the influence function on the space of persistence diagrams, we establish the proposed framework to be less sensitive to outliers. The robust persistence diagrams are shown to be consistent estimators in bottleneck distance, with the convergence rate controlled by the smoothness of the kernel. This, in turn, allows us to construct uniform confidence bands in the space of persistence diagrams. Finally, we demonstrate the superiority of the proposed approach on benchmark datasets.