Modified Loss of Momentum Gradient Descent: Fine-Grained Analysis

We analyze gradient descent with Polyak heavy-ball momentum (HB) whose fixed momentum parameter $\beta \in (0, 1)$ provides exponential decay of memory. Building on Kovachki and Stuart (2021), we prove that on an exponentially attractive invariant manifold the algorithm is exactly plain gradient descent with a modified loss, provided that the step size $h$ is small enough. Although the modified loss does not admit a closed-form expression, we describe it with arbitrary precision and prove global (finite "time" horizon) approximation bounds $O(h^{R})$ for any finite order $R \geq 2$. We then conduct a fine-grained analysis of the combinatorics underlying the memoryless approximations of HB, in particular, finding a rich family of polynomials in $\beta$ hidden inside which contains Eulerian and Narayana polynomials. We derive continuous modified equations of arbitrary approximation order (with rigorous bounds) and the principal flow that approximates the HB dynamics, generalizing Rosca et al. (2023). Approximation theorems cover both full-batch and mini-batch HB. Our theoretical results shed new light on the main features of gradient descent with heavy-ball momentum, and outline a road-map for similar analysis of other optimization algorithms.

How Memory in Optimization Algorithms Implicitly Modifies the Loss

In modern optimization methods used in deep learning, each update depends on the history of previous iterations, often referred to as memory, and this dependence decays fast as the iterates go further into the past. For example, gradient descent with momentum has exponentially decaying memory through exponentially averaged past gradients. We introduce a general technique for identifying a memoryless algorithm that approximates an optimization algorithm with memory. It is obtained by replacing all past iterates in the update by the current one, and then adding a correction term arising from memory (also a function of the current iterate). This correction term can be interpreted as a perturbation of the loss, and the nature of this perturbation can inform how memory implicitly (anti-)regularizes the optimization dynamics. As an application of our theory, we find that Lion does not have the kind of implicit anti-regularization induced by memory that AdamW does, providing a theory-based explanation for Lion's better generalization performance recently documented.

Inference with Mondrian Random Forests

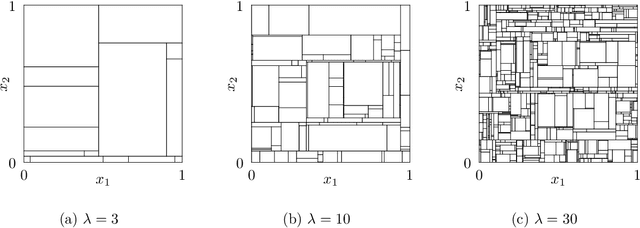
Random forests are popular methods for classification and regression, and many different variants have been proposed in recent years. One interesting example is the Mondrian random forest, in which the underlying trees are constructed according to a Mondrian process. In this paper we give a central limit theorem for the estimates made by a Mondrian random forest in the regression setting. When combined with a bias characterization and a consistent variance estimator, this allows one to perform asymptotically valid statistical inference, such as constructing confidence intervals, on the unknown regression function. We also provide a debiasing procedure for Mondrian random forests which allows them to achieve minimax-optimal estimation rates with $\beta$-H\"older regression functions, for all $\beta$ and in arbitrary dimension, assuming appropriate parameter tuning.

On the Implicit Bias of Adam

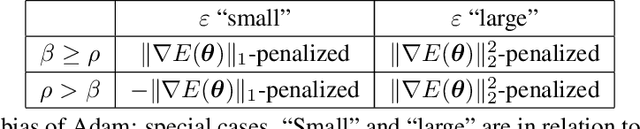
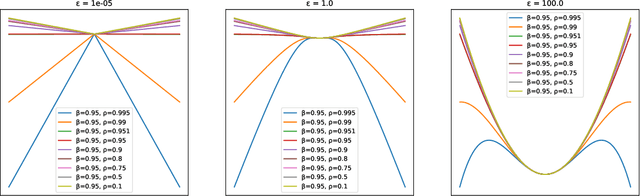
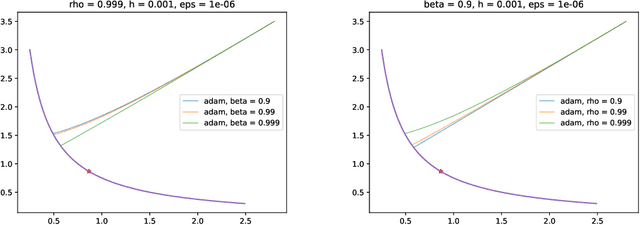
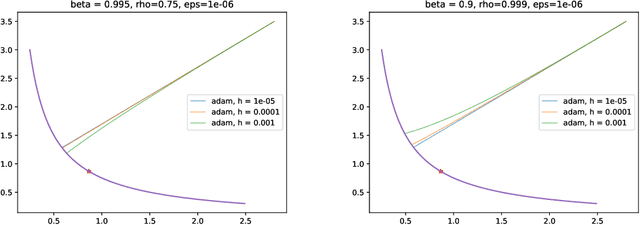
In previous literature, backward error analysis was used to find ordinary differential equations (ODEs) approximating the gradient descent trajectory. It was found that finite step sizes implicitly regularize solutions because terms appearing in the ODEs penalize the two-norm of the loss gradients. We prove that the existence of similar implicit regularization in RMSProp and Adam depends on their hyperparameters and the training stage, but with a different "norm" involved: the corresponding ODE terms either penalize the (perturbed) one-norm of the loss gradients or, on the contrary, hinder its decrease (the latter case being typical). We also conduct numerical experiments and discuss how the proven facts can influence generalization.

On the Pointwise Behavior of Recursive Partitioning and Its Implications for Heterogeneous Causal Effect Estimation

Decision tree learning is increasingly being used for pointwise inference. Important applications include causal heterogenous treatment effects and dynamic policy decisions, as well as conditional quantile regression and design of experiments, where tree estimation and inference is conducted at specific values of the covariates. In this paper, we call into question the use of decision trees (trained by adaptive recursive partitioning) for such purposes by demonstrating that they can fail to achieve polynomial rates of convergence in uniform norm, even with pruning. Instead, the convergence may be poly-logarithmic or, in some important special cases, such as honest regression trees, fail completely. We show that random forests can remedy the situation, turning poor performing trees into nearly optimal procedures, at the cost of losing interpretability and introducing two additional tuning parameters. The two hallmarks of random forests, subsampling and the random feature selection mechanism, are seen to each distinctively contribute to achieving nearly optimal performance for the model class considered.

On Binscatter

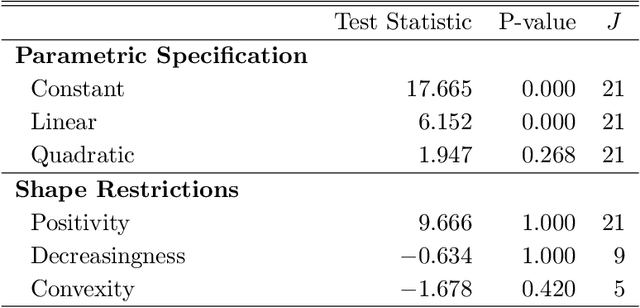
Binscatter is very popular in applied microeconomics. It provides a flexible, yet parsimonious way of visualizing and summarizing large data sets in regression settings, and it is often used for informal evaluation of substantive hypotheses such as linearity or monotonicity of the regression function. This paper presents a foundational, thorough analysis of binscatter: we give an array of theoretical and practical results that aid both in understanding current practices (i.e., their validity or lack thereof) and in offering theory-based guidance for future applications. Our main results include principled number of bins selection, confidence intervals and bands, hypothesis tests for parametric and shape restrictions of the regression function, and several other new methods, applicable to canonical binscatter as well as higher-order polynomial, covariate-adjusted and smoothness-restricted extensions thereof. In particular, we highlight important methodological problems related to covariate adjustment methods used in current practice. We also discuss extensions to clustered data. Our results are illustrated with simulated and real data throughout. Companion general-purpose software packages for \texttt{Stata} and \texttt{R} are provided. Finally, from a technical perspective, new theoretical results for partitioning-based series estimation are obtained that may be of independent interest.