On Binscatter
Paper and Code
Feb 25, 2019


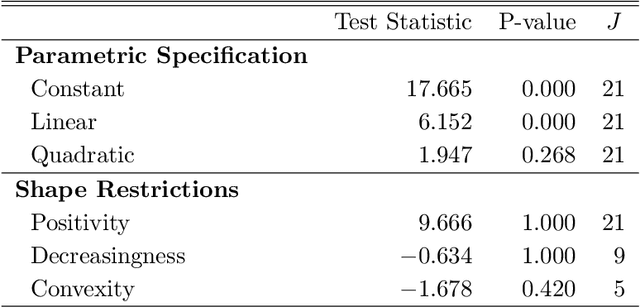
Binscatter is very popular in applied microeconomics. It provides a flexible, yet parsimonious way of visualizing and summarizing large data sets in regression settings, and it is often used for informal evaluation of substantive hypotheses such as linearity or monotonicity of the regression function. This paper presents a foundational, thorough analysis of binscatter: we give an array of theoretical and practical results that aid both in understanding current practices (i.e., their validity or lack thereof) and in offering theory-based guidance for future applications. Our main results include principled number of bins selection, confidence intervals and bands, hypothesis tests for parametric and shape restrictions of the regression function, and several other new methods, applicable to canonical binscatter as well as higher-order polynomial, covariate-adjusted and smoothness-restricted extensions thereof. In particular, we highlight important methodological problems related to covariate adjustment methods used in current practice. We also discuss extensions to clustered data. Our results are illustrated with simulated and real data throughout. Companion general-purpose software packages for \texttt{Stata} and \texttt{R} are provided. Finally, from a technical perspective, new theoretical results for partitioning-based series estimation are obtained that may be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge