TSUBF-Net: Trans-Spatial UNet-like Network with Bi-direction Fusion for Segmentation of Adenoid Hypertrophy in CT

Adenoid hypertrophy stands as a common cause of obstructive sleep apnea-hypopnea syndrome in children. It is characterized by snoring, nasal congestion, and growth disorders. Computed Tomography (CT) emerges as a pivotal medical imaging modality, utilizing X-rays and advanced computational techniques to generate detailed cross-sectional images. Within the realm of pediatric airway assessments, CT imaging provides an insightful perspective on the shape and volume of enlarged adenoids. Despite the advances of deep learning methods for medical imaging analysis, there remains an emptiness in the segmentation of adenoid hypertrophy in CT scans. To address this research gap, we introduce TSUBF-Nett (Trans-Spatial UNet-like Network based on Bi-direction Fusion), a 3D medical image segmentation framework. TSUBF-Net is engineered to effectively discern intricate 3D spatial interlayer features in CT scans and enhance the extraction of boundary-blurring features. Notably, we propose two innovative modules within the U-shaped network architecture:the Trans-Spatial Perception module (TSP) and the Bi-directional Sampling Collaborated Fusion module (BSCF).These two modules are in charge of operating during the sampling process and strategically fusing down-sampled and up-sampled features, respectively. Furthermore, we introduce the Sobel loss term, which optimizes the smoothness of the segmentation results and enhances model accuracy. Extensive 3D segmentation experiments are conducted on several datasets. TSUBF-Net is superior to the state-of-the-art methods with the lowest HD95: 7.03, IoU:85.63, and DSC: 92.26 on our own AHSD dataset. The results in the other two public datasets also demonstrate that our methods can robustly and effectively address the challenges of 3D segmentation in CT scans.

Large language models improve Alzheimer's disease diagnosis using multi-modality data

In diagnosing challenging conditions such as Alzheimer's disease (AD), imaging is an important reference. Non-imaging patient data such as patient information, genetic data, medication information, cognitive and memory tests also play a very important role in diagnosis. Effect. However, limited by the ability of artificial intelligence models to mine such information, most of the existing models only use multi-modal image data, and cannot make full use of non-image data. We use a currently very popular pre-trained large language model (LLM) to enhance the model's ability to utilize non-image data, and achieved SOTA results on the ADNI dataset.

Causal Inference in Possibly Nonlinear Factor Models

This paper develops a general causal inference method for treatment effects models under selection on unobservables. A large set of covariates that admits an unknown, possibly nonlinear factor structure is exploited to control for the latent confounders. The key building block is a local principal subspace approximation procedure that combines $K$-nearest neighbors matching and principal component analysis. Estimators of many causal parameters, including average treatment effects and counterfactual distributions, are constructed based on doubly-robust score functions. Large-sample properties of these estimators are established, which only require relatively mild conditions on the principal subspace approximation. The results are illustrated with an empirical application studying the effect of political connections on stock returns of financial firms, and a Monte Carlo experiment. The main technical and methodological results regarding the general local principal subspace approximation method may be of independent interest.

On Binscatter

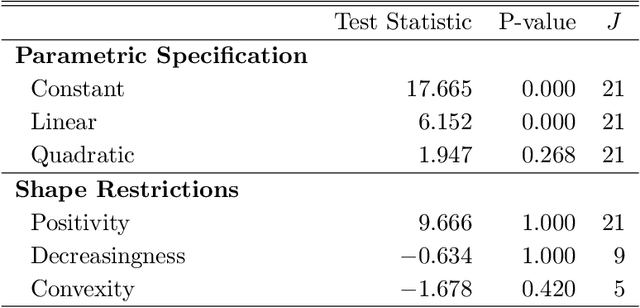
Binscatter is very popular in applied microeconomics. It provides a flexible, yet parsimonious way of visualizing and summarizing large data sets in regression settings, and it is often used for informal evaluation of substantive hypotheses such as linearity or monotonicity of the regression function. This paper presents a foundational, thorough analysis of binscatter: we give an array of theoretical and practical results that aid both in understanding current practices (i.e., their validity or lack thereof) and in offering theory-based guidance for future applications. Our main results include principled number of bins selection, confidence intervals and bands, hypothesis tests for parametric and shape restrictions of the regression function, and several other new methods, applicable to canonical binscatter as well as higher-order polynomial, covariate-adjusted and smoothness-restricted extensions thereof. In particular, we highlight important methodological problems related to covariate adjustment methods used in current practice. We also discuss extensions to clustered data. Our results are illustrated with simulated and real data throughout. Companion general-purpose software packages for \texttt{Stata} and \texttt{R} are provided. Finally, from a technical perspective, new theoretical results for partitioning-based series estimation are obtained that may be of independent interest.