On the Pointwise Behavior of Recursive Partitioning and Its Implications for Heterogeneous Causal Effect Estimation

Decision tree learning is increasingly being used for pointwise inference. Important applications include causal heterogenous treatment effects and dynamic policy decisions, as well as conditional quantile regression and design of experiments, where tree estimation and inference is conducted at specific values of the covariates. In this paper, we call into question the use of decision trees (trained by adaptive recursive partitioning) for such purposes by demonstrating that they can fail to achieve polynomial rates of convergence in uniform norm, even with pruning. Instead, the convergence may be poly-logarithmic or, in some important special cases, such as honest regression trees, fail completely. We show that random forests can remedy the situation, turning poor performing trees into nearly optimal procedures, at the cost of losing interpretability and introducing two additional tuning parameters. The two hallmarks of random forests, subsampling and the random feature selection mechanism, are seen to each distinctively contribute to achieving nearly optimal performance for the model class considered.

Nonparametric Variable Screening with Optimal Decision Stumps

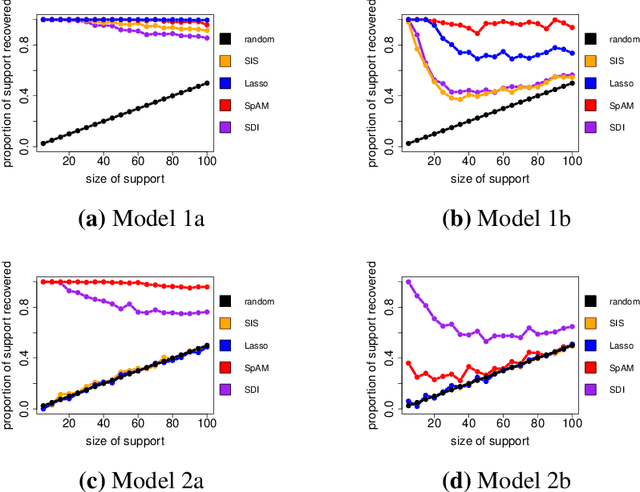
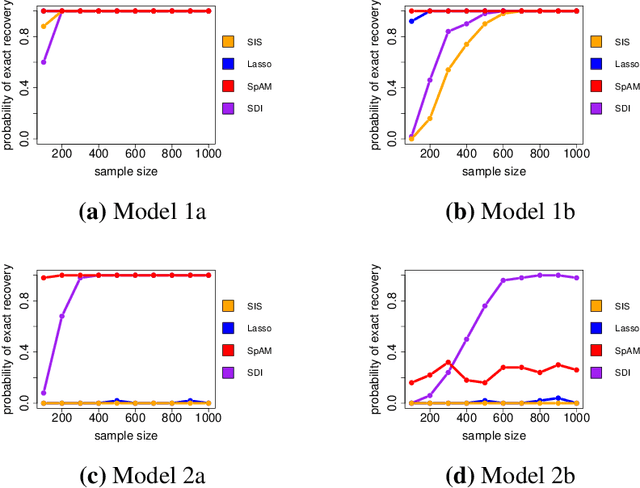
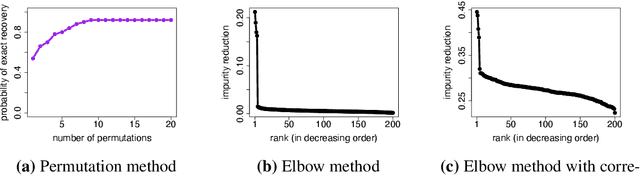
Decision trees and their ensembles are endowed with a rich set of diagnostic tools for ranking and screening input variables in a predictive model. One of the most commonly used in practice is the Mean Decrease in Impurity (MDI), which calculates an importance score for a variable by summing the weighted impurity reductions over all non-terminal nodes split with that variable. Despite the widespread use of tree based variable importance measures such as MDI, pinning down their theoretical properties has been challenging and therefore largely unexplored. To address this gap between theory and practice, we derive rigorous finite sample performance guarantees for variable ranking and selection in nonparametric models with MDI for a single-level CART decision tree (decision stump). We find that the marginal signal strength of each variable and ambient dimensionality can be considerably weaker and higher, respectively, than state-of-the-art nonparametric variable selection methods. Furthermore, unlike previous marginal screening methods that attempt to directly estimate each marginal projection via a truncated basis expansion, the fitted model used here is a simple, parsimonious decision stump, thereby eliminating the need for tuning the number of basis terms. Thus, surprisingly, even though decision stumps are highly inaccurate for estimation purposes, they can still be used to perform consistent model selection.