Yulia Baker
Feature Selection for Data Integration with Mixed Multi-view Data
Mar 27, 2019
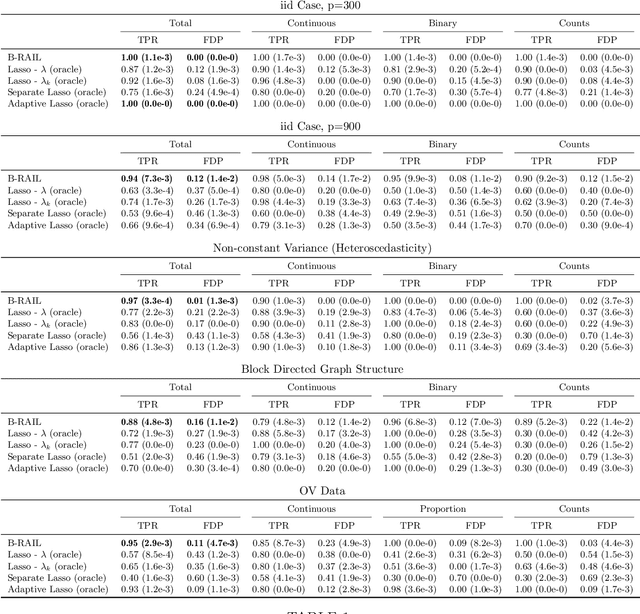
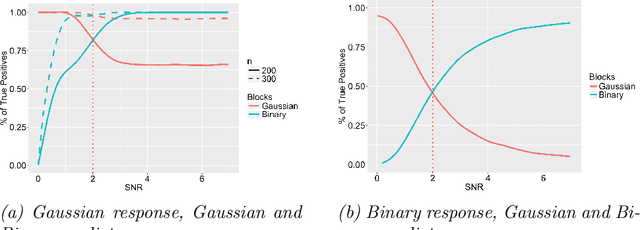
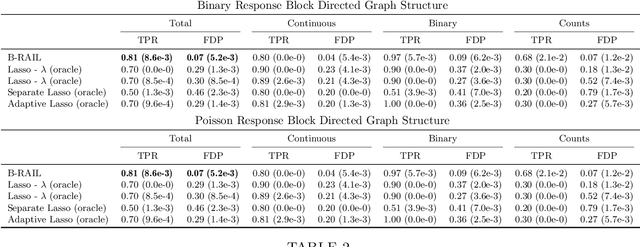
Abstract:Data integration methods that analyze multiple sources of data simultaneously can often provide more holistic insights than can separate inquiries of each data source. Motivated by the advantages of data integration in the era of "big data", we investigate feature selection for high-dimensional multi-view data with mixed data types (e.g. continuous, binary, count-valued). This heterogeneity of multi-view data poses numerous challenges for existing feature selection methods. However, after critically examining these issues through empirical and theoretically-guided lenses, we develop a practical solution, the Block Randomized Adaptive Iterative Lasso (B-RAIL), which combines the strengths of the randomized Lasso, adaptive weighting schemes, and stability selection. B-RAIL serves as a versatile data integration method for sparse regression and graph selection, and we demonstrate the effectiveness of B-RAIL through extensive simulations and a case study to infer the ovarian cancer gene regulatory network. In this case study, B-RAIL successfully identifies well-known biomarkers associated with ovarian cancer and hints at novel candidates for future ovarian cancer research.
A General Framework for Mixed Graphical Models
Nov 02, 2014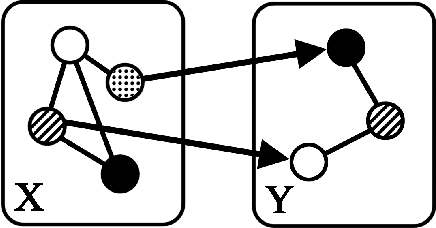
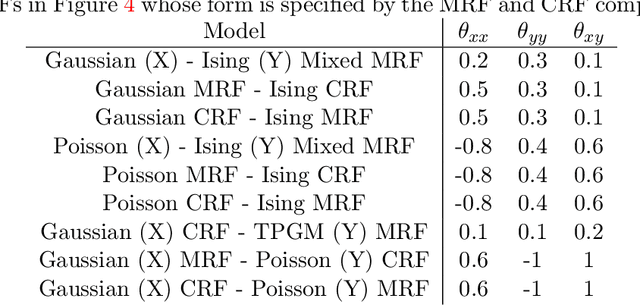
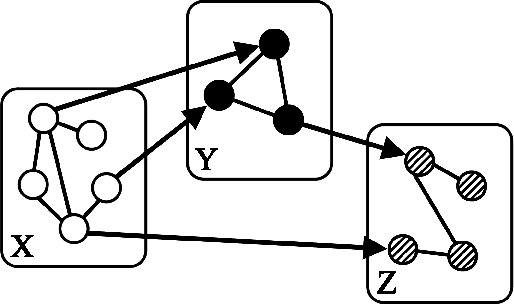
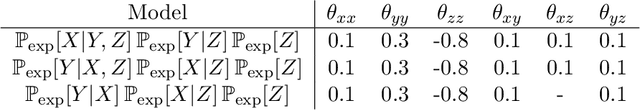
Abstract:"Mixed Data" comprising a large number of heterogeneous variables (e.g. count, binary, continuous, skewed continuous, among other data types) are prevalent in varied areas such as genomics and proteomics, imaging genetics, national security, social networking, and Internet advertising. There have been limited efforts at statistically modeling such mixed data jointly, in part because of the lack of computationally amenable multivariate distributions that can capture direct dependencies between such mixed variables of different types. In this paper, we address this by introducing a novel class of Block Directed Markov Random Fields (BDMRFs). Using the basic building block of node-conditional univariate exponential families from Yang et al. (2012), we introduce a class of mixed conditional random field distributions, that are then chained according to a block-directed acyclic graph to form our class of Block Directed Markov Random Fields (BDMRFs). The Markov independence graph structure underlying a BDMRF thus has both directed and undirected edges. We introduce conditions under which these distributions exist and are normalizable, study several instances of our models, and propose scalable penalized conditional likelihood estimators with statistical guarantees for recovering the underlying network structure. Simulations as well as an application to learning mixed genomic networks from next generation sequencing expression data and mutation data demonstrate the versatility of our methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge