Survey and Improvement Strategies for Gene Prioritization with Large Language Models

Rare diseases are challenging to diagnose due to limited patient data and genetic diversity. Despite advances in variant prioritization, many cases remain undiagnosed. While large language models (LLMs) have performed well in medical exams, their effectiveness in diagnosing rare genetic diseases has not been assessed. To identify causal genes, we benchmarked various LLMs for gene prioritization. Using multi-agent and Human Phenotype Ontology (HPO) classification, we categorized patients based on phenotypes and solvability levels. As gene set size increased, LLM performance deteriorated, so we used a divide-and-conquer strategy to break the task into smaller subsets. At baseline, GPT-4 outperformed other LLMs, achieving near 30% accuracy in ranking causal genes correctly. The multi-agent and HPO approaches helped distinguish confidently solved cases from challenging ones, highlighting the importance of known gene-phenotype associations and phenotype specificity. We found that cases with specific phenotypes or clear associations were more accurately solved. However, we observed biases toward well-studied genes and input order sensitivity, which hindered gene prioritization. Our divide-and-conquer strategy improved accuracy by overcoming these biases. By utilizing HPO classification, novel multi-agent techniques, and our LLM strategy, we improved causal gene identification accuracy compared to our baseline evaluation. This approach streamlines rare disease diagnosis, facilitates reanalysis of unsolved cases, and accelerates gene discovery, supporting the development of targeted diagnostics and therapies.

Assessing and Enhancing Large Language Models in Rare Disease Question-answering

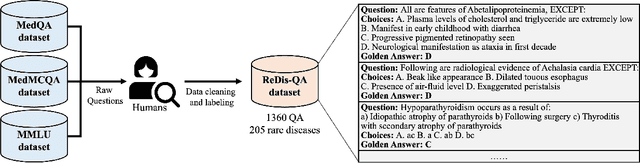
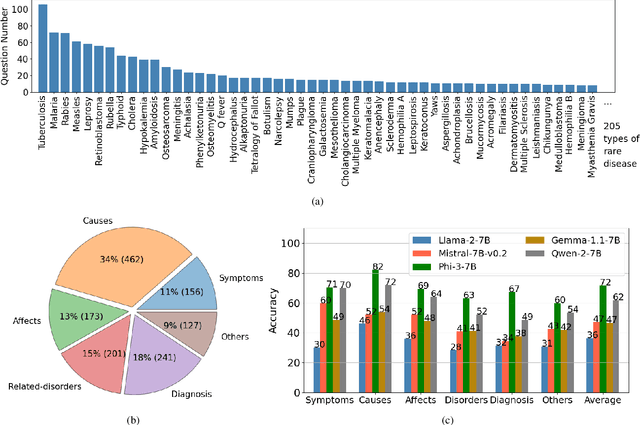
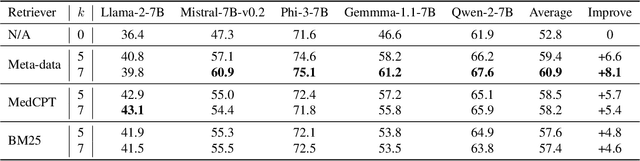
Despite the impressive capabilities of Large Language Models (LLMs) in general medical domains, questions remain about their performance in diagnosing rare diseases. To answer this question, we aim to assess the diagnostic performance of LLMs in rare diseases, and explore methods to enhance their effectiveness in this area. In this work, we introduce a rare disease question-answering (ReDis-QA) dataset to evaluate the performance of LLMs in diagnosing rare diseases. Specifically, we collected 1360 high-quality question-answer pairs within the ReDis-QA dataset, covering 205 rare diseases. Additionally, we annotated meta-data for each question, facilitating the extraction of subsets specific to any given disease and its property. Based on the ReDis-QA dataset, we benchmarked several open-source LLMs, revealing that diagnosing rare diseases remains a significant challenge for these models. To facilitate retrieval augmentation generation for rare disease diagnosis, we collect the first rare diseases corpus (ReCOP), sourced from the National Organization for Rare Disorders (NORD) database. Specifically, we split the report of each rare disease into multiple chunks, each representing a different property of the disease, including their overview, symptoms, causes, effects, related disorders, diagnosis, and standard therapies. This structure ensures that the information within each chunk aligns consistently with a question. Experiment results demonstrate that ReCOP can effectively improve the accuracy of LLMs on the ReDis-QA dataset by an average of 8%. Moreover, it significantly guides LLMs to generate trustworthy answers and explanations that can be traced back to existing literature.

On Graphical Models via Univariate Exponential Family Distributions

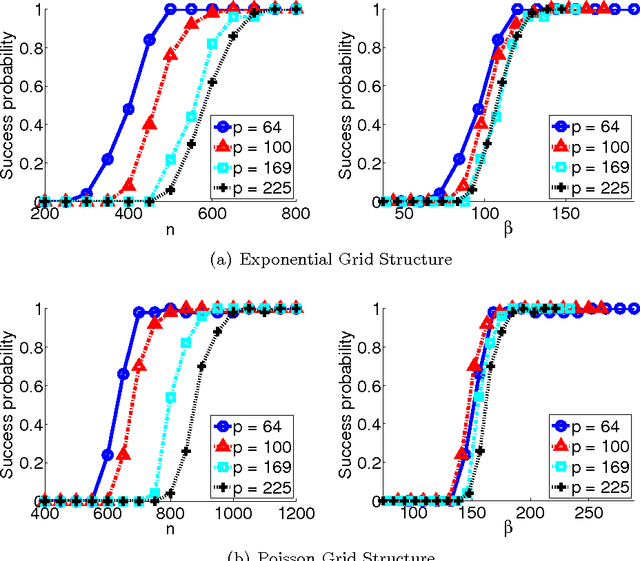
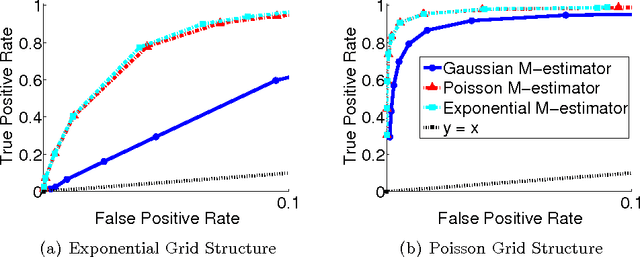
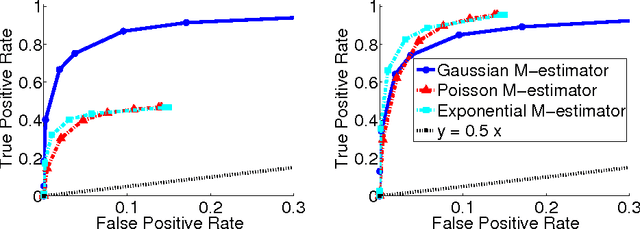
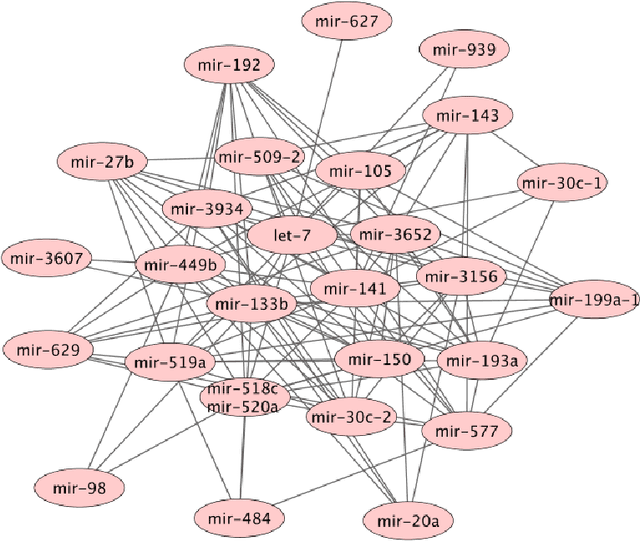
Undirected graphical models, or Markov networks, are a popular class of statistical models, used in a wide variety of applications. Popular instances of this class include Gaussian graphical models and Ising models. In many settings, however, it might not be clear which subclass of graphical models to use, particularly for non-Gaussian and non-categorical data. In this paper, we consider a general sub-class of graphical models where the node-wise conditional distributions arise from exponential families. This allows us to derive multivariate graphical model distributions from univariate exponential family distributions, such as the Poisson, negative binomial, and exponential distributions. Our key contributions include a class of M-estimators to fit these graphical model distributions; and rigorous statistical analysis showing that these M-estimators recover the true graphical model structure exactly, with high probability. We provide examples of genomic and proteomic networks learned via instances of our class of graphical models derived from Poisson and exponential distributions.

A General Framework for Mixed Graphical Models

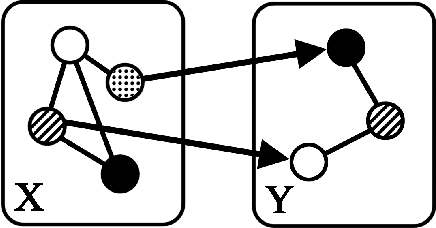
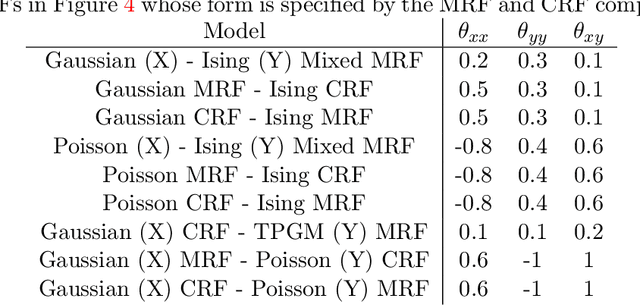
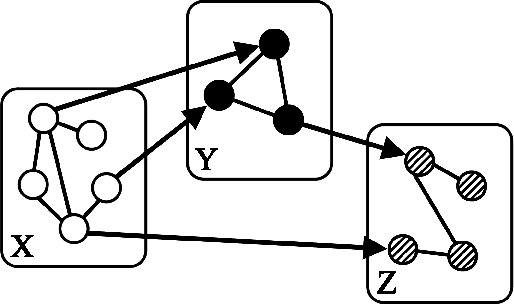
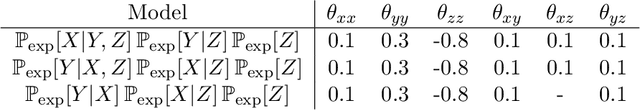
"Mixed Data" comprising a large number of heterogeneous variables (e.g. count, binary, continuous, skewed continuous, among other data types) are prevalent in varied areas such as genomics and proteomics, imaging genetics, national security, social networking, and Internet advertising. There have been limited efforts at statistically modeling such mixed data jointly, in part because of the lack of computationally amenable multivariate distributions that can capture direct dependencies between such mixed variables of different types. In this paper, we address this by introducing a novel class of Block Directed Markov Random Fields (BDMRFs). Using the basic building block of node-conditional univariate exponential families from Yang et al. (2012), we introduce a class of mixed conditional random field distributions, that are then chained according to a block-directed acyclic graph to form our class of Block Directed Markov Random Fields (BDMRFs). The Markov independence graph structure underlying a BDMRF thus has both directed and undirected edges. We introduce conditions under which these distributions exist and are normalizable, study several instances of our models, and propose scalable penalized conditional likelihood estimators with statistical guarantees for recovering the underlying network structure. Simulations as well as an application to learning mixed genomic networks from next generation sequencing expression data and mutation data demonstrate the versatility of our methods.