Faster Convex Lipschitz Regression via 2-block ADMM

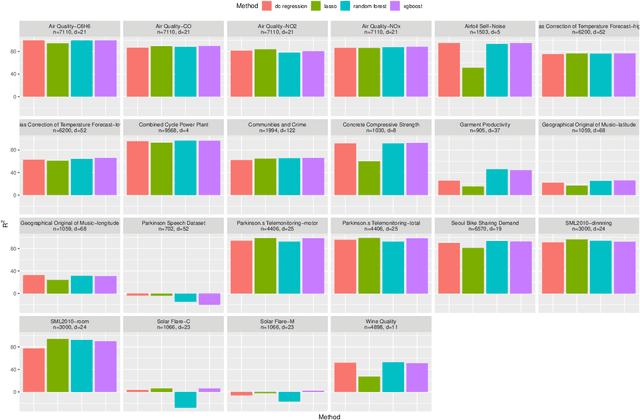
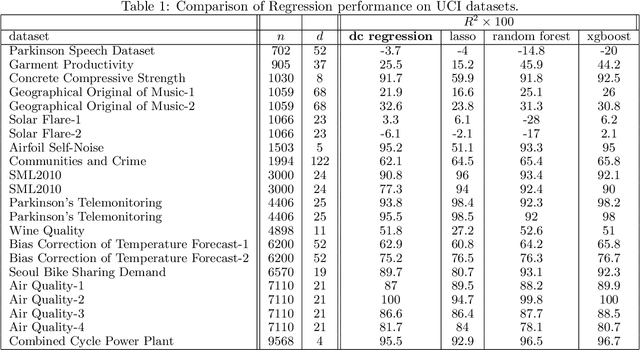
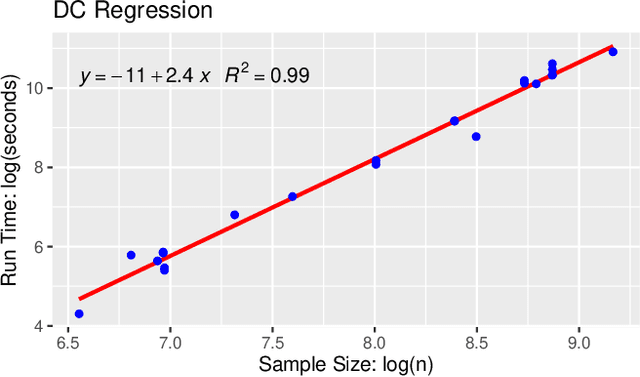
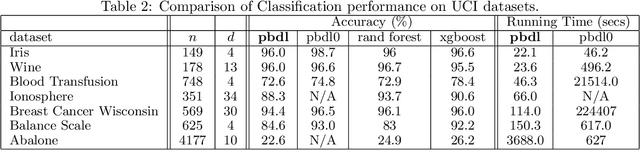
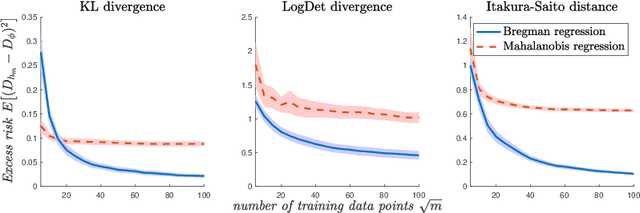
The task of approximating an arbitrary convex function arises in several learning problems such as convex regression, learning with a difference of convex (DC) functions, and approximating Bregman divergences. In this paper, we show how a broad class of convex function learning problems can be solved via a 2-block ADMM approach, where updates for each block can be computed in closed form. For the task of convex Lipschitz regression, we establish that our proposed algorithm converges with iteration complexity of $ O(n\sqrt{d}/\epsilon)$ for a dataset $ X \in \mathbb R^{n\times d}$ and $\epsilon > 0$. Combined with per-iteration computation complexity, our method converges with the rate $O(n^3 d^{1.5}/\epsilon+n^2 d^{2.5}/\epsilon+n d^3/\epsilon)$. This new rate improves the state of the art rate of $O(n^5d^2/\epsilon)$ available by interior point methods if $d = o( n^4)$. Further we provide similar solvers for DC regression and Bregman divergence learning. Unlike previous approaches, our method is amenable to the use of GPUs. We demonstrate on regression and metric learning experiments that our approach is up to 30 times faster than the existing method, and produces results that are comparable to state-of-the-art.

Piecewise Linear Regression via a Difference of Convex Functions

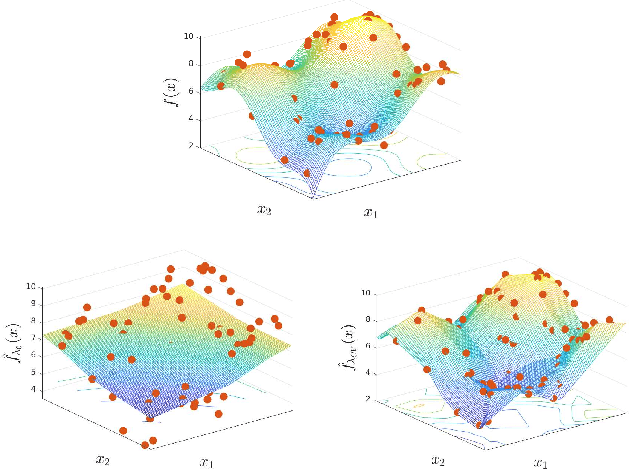
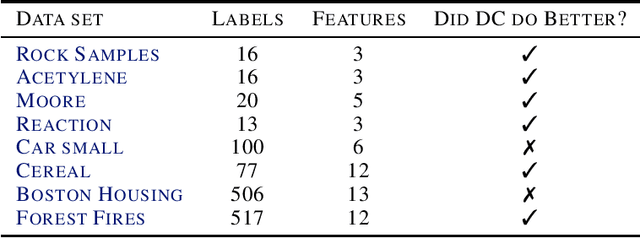
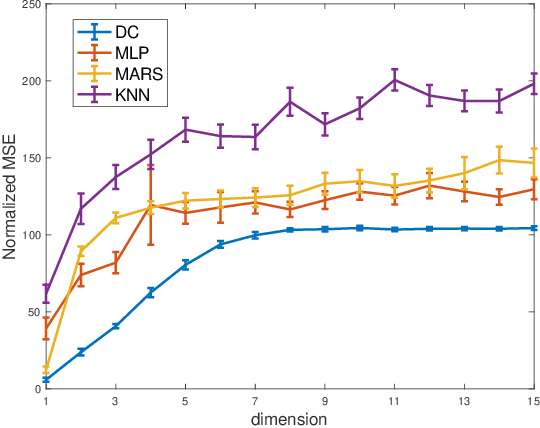
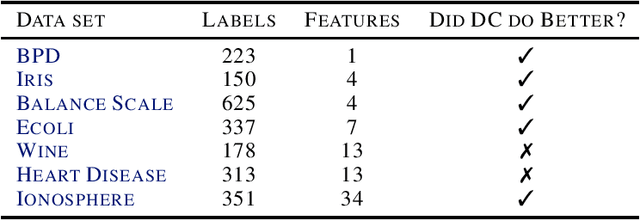
We present a new piecewise linear regression methodology that utilizes fitting a difference of convex functions (DC functions) to the data. These are functions $f$ that may be represented as the difference $\phi_1 - \phi_2$ for a choice of convex functions $\phi_1, \phi_2$. The method proceeds by estimating piecewise-liner convex functions, in a manner similar to max-affine regression, whose difference approximates the data. The choice of the function is regularised by a new seminorm over the class of DC functions that controls the $\ell_\infty$ Lipschitz constant of the estimate. The resulting methodology can be efficiently implemented via Quadratic programming even in high dimensions, and is shown to have close to minimax statistical risk. We empirically validate the method, showing it to be practically implementable, and to have comparable performance to existing regression/classification methods on real-world datasets.

Learning Bregman Divergences

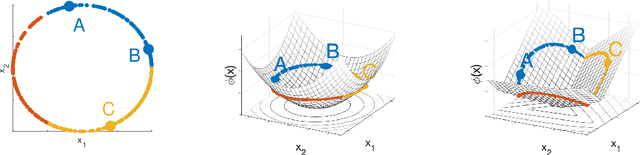
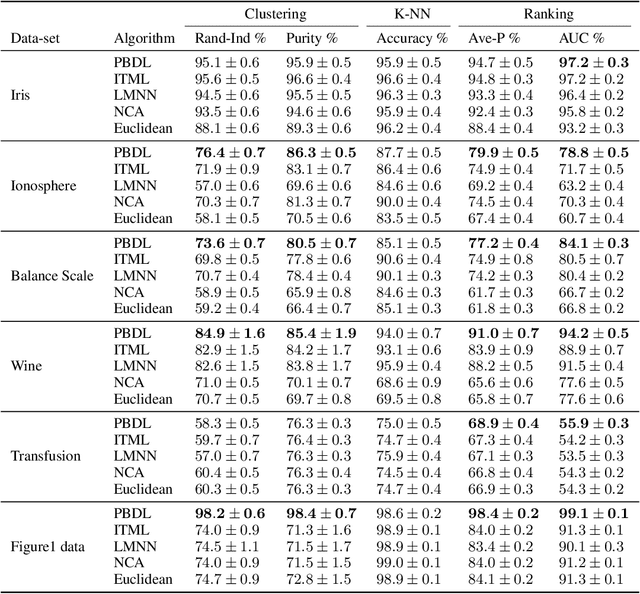
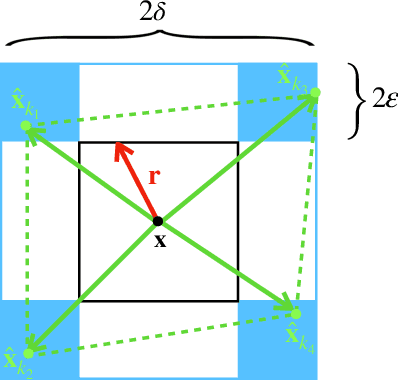
Metric learning is the problem of learning a task-specific distance function given supervision. Classical linear methods for this problem (known as Mahalanobis metric learning approaches) are well-studied both theoretically and empirically, but are limited to Euclidean distances after learned linear transformations of the input space. In this paper, we consider learning a Bregman divergence, a rich and important class of divergences that includes Mahalanobis metrics as a special case but also includes the KL-divergence and others. We develop a formulation and algorithm for learning arbitrary Bregman divergences based on approximating their underlying convex generating function via a piecewise linear function. We show several theoretical results of our resulting model, including a PAC guarantee that the learned Bregman divergence approximates an arbitrary Bregman divergence with error O_p (m^(-1/(d+2))), where m is the number of training points and d is the dimension of the data. We provide empirical results on using the learned divergences for classification, semi-supervised clustering, and ranking problems.

Conditioning Deep Generative Raw Audio Models for Structured Automatic Music

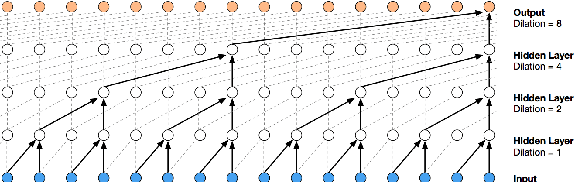
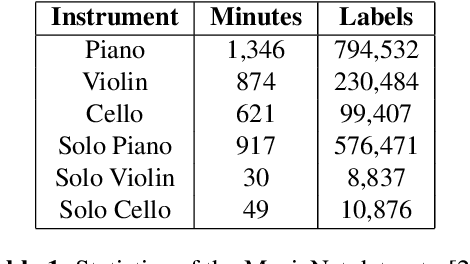
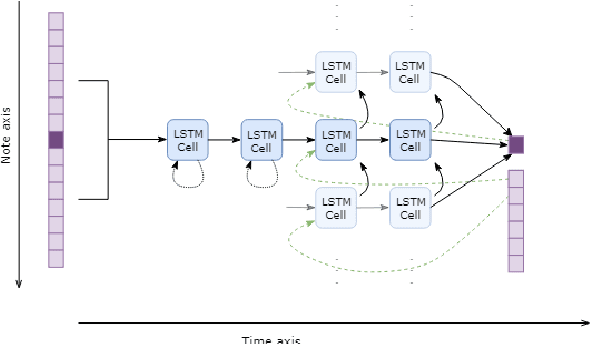
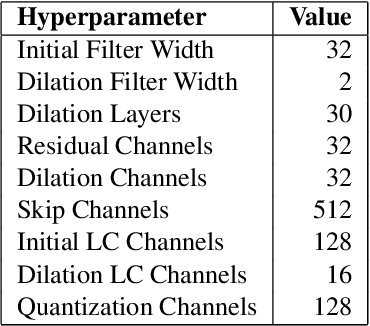
Existing automatic music generation approaches that feature deep learning can be broadly classified into two types: raw audio models and symbolic models. Symbolic models, which train and generate at the note level, are currently the more prevalent approach; these models can capture long-range dependencies of melodic structure, but fail to grasp the nuances and richness of raw audio generations. Raw audio models, such as DeepMind's WaveNet, train directly on sampled audio waveforms, allowing them to produce realistic-sounding, albeit unstructured music. In this paper, we propose an automatic music generation methodology combining both of these approaches to create structured, realistic-sounding compositions. We consider a Long Short Term Memory network to learn the melodic structure of different styles of music, and then use the unique symbolic generations from this model as a conditioning input to a WaveNet-based raw audio generator, creating a model for automatic, novel music. We then evaluate this approach by showcasing results of this work.