Learning Bregman Divergences
Paper and Code
Jun 06, 2019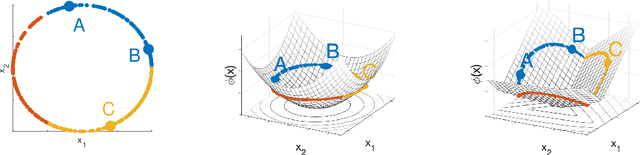
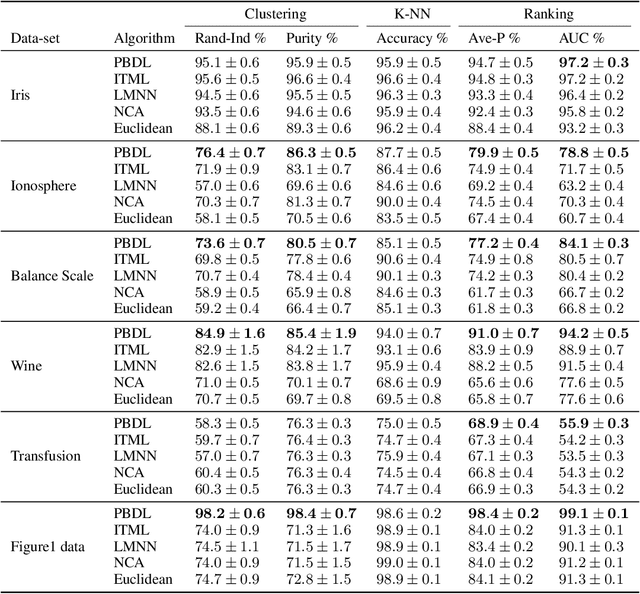
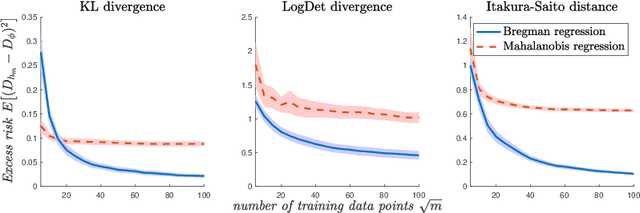
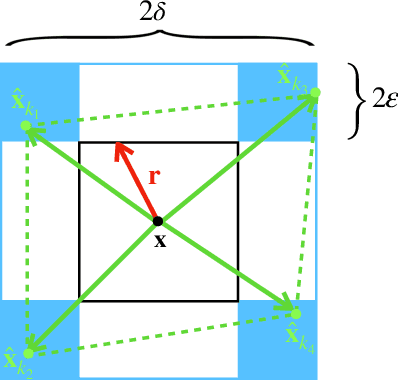
Metric learning is the problem of learning a task-specific distance function given supervision. Classical linear methods for this problem (known as Mahalanobis metric learning approaches) are well-studied both theoretically and empirically, but are limited to Euclidean distances after learned linear transformations of the input space. In this paper, we consider learning a Bregman divergence, a rich and important class of divergences that includes Mahalanobis metrics as a special case but also includes the KL-divergence and others. We develop a formulation and algorithm for learning arbitrary Bregman divergences based on approximating their underlying convex generating function via a piecewise linear function. We show several theoretical results of our resulting model, including a PAC guarantee that the learned Bregman divergence approximates an arbitrary Bregman divergence with error O_p (m^(-1/(d+2))), where m is the number of training points and d is the dimension of the data. We provide empirical results on using the learned divergences for classification, semi-supervised clustering, and ranking problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge