Edge-Colored Clustering in Hypergraphs: Beyond Minimizing Unsatisfied Edges

We consider a framework for clustering edge-colored hypergraphs, where the goal is to cluster (equivalently, to color) objects based on the primary type of multiway interactions they participate in. One well-studied objective is to color nodes to minimize the number of unsatisfied hyperedges -- those containing one or more nodes whose color does not match the hyperedge color. We motivate and present advances for several directions that extend beyond this minimization problem. We first provide new algorithms for maximizing satisfied edges, which is the same at optimality but is much more challenging to approximate, with all prior work restricted to graphs. We develop the first approximation algorithm for hypergraphs, and then refine it to improve the best-known approximation factor for graphs. We then introduce new objective functions that incorporate notions of balance and fairness, and provide new hardness results, approximations, and fixed-parameter tractability results.

Graph Inspection for Robotic Motion Planning: Do Arithmetic Circuits Help?

We investigate whether algorithms based on arithmetic circuits are a viable alternative to existing solvers for Graph Inspection, a problem with direct application in robotic motion planning. Specifically, we seek to address the high memory usage of existing solvers. Aided by novel theoretical results enabling fast solution recovery, we implement a circuit-based solver for Graph Inspection which uses only polynomial space and test it on several realistic robotic motion planning datasets. In particular, we provide a comprehensive experimental evaluation of a suite of engineered algorithms for three key subroutines. While this evaluation demonstrates that circuit-based methods are not yet practically competitive for our robotics application, it also provides insights which may guide future efforts to bring circuit-based algorithms from theory to practice.

Leveraging Fixed-Parameter Tractability for Robot Inspection Planning

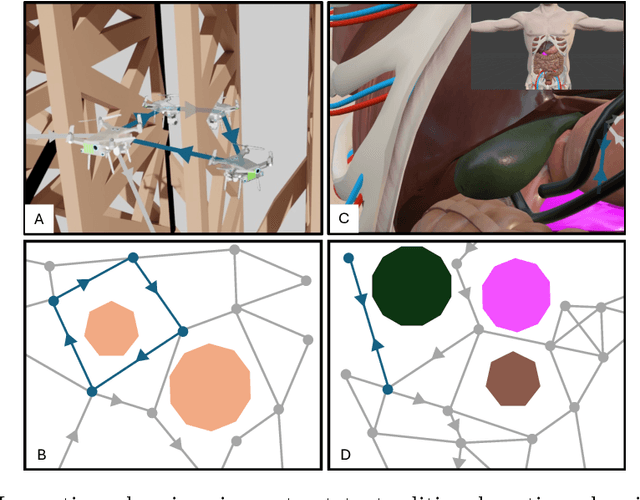
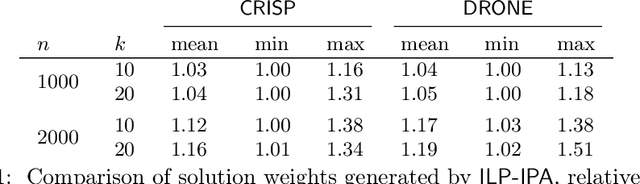
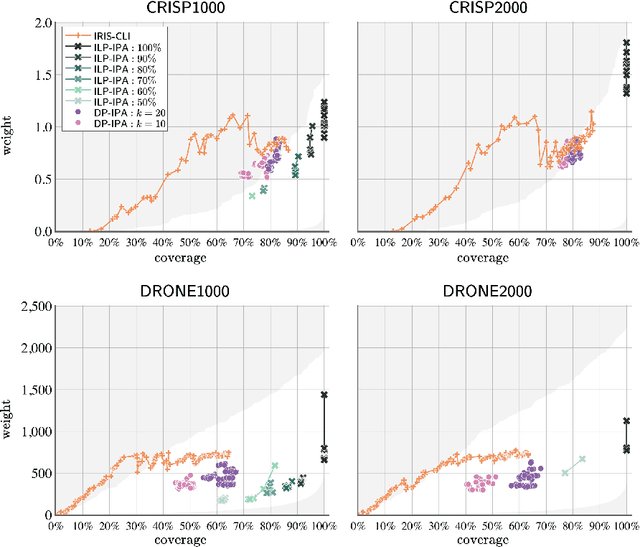
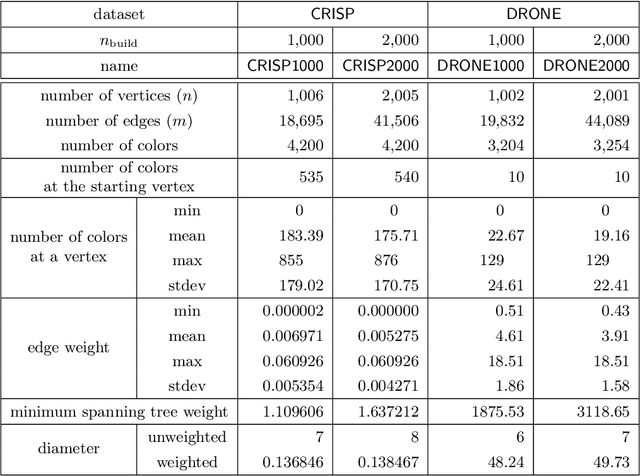
Autonomous robotic inspection, where a robot moves through its environment and inspects points of interest, has applications in industrial settings, structural health monitoring, and medicine. Planning the paths for a robot to safely and efficiently perform such an inspection is an extremely difficult algorithmic challenge. In this work we consider an abstraction of the inspection planning problem which we term Graph Inspection. We give two exact algorithms for this problem, using dynamic programming and integer linear programming. We analyze the performance of these methods, and present multiple approaches to achieve scalability. We demonstrate significant improvement both in path weight and inspection coverage over a state-of-the-art approach on two robotics tasks in simulation, a bridge inspection task by a UAV and a surgical inspection task using a medical robot.