Better Learning-Augmented Spanning Tree Algorithms via Metric Forest Completion

We present improved learning-augmented algorithms for finding an approximate minimum spanning tree (MST) for points in an arbitrary metric space. Our work follows a recent framework called metric forest completion (MFC), where the learned input is a forest that must be given additional edges to form a full spanning tree. Veldt et al. (2025) showed that optimally completing the forest takes $Ω(n^2)$ time, but designed a 2.62-approximation for MFC with subquadratic complexity. The same method is a $(2γ+ 1)$-approximation for the original MST problem, where $γ\geq 1$ is a quality parameter for the initial forest. We introduce a generalized method that interpolates between this prior algorithm and an optimal $Ω(n^2)$-time MFC algorithm. Our approach considers only edges incident to a growing number of strategically chosen ``representative'' points. One corollary of our analysis is to improve the approximation factor of the previous algorithm from 2.62 for MFC and $(2γ+1)$ for metric MST to 2 and $2γ$ respectively. We prove this is tight for worst-case instances, but we still obtain better instance-specific approximations using our generalized method. We complement our theoretical results with a thorough experimental evaluation.

Approximate Tree Completion and Learning-Augmented Algorithms for Metric Minimum Spanning Trees

Finding a minimum spanning tree (MST) for $n$ points in an arbitrary metric space is a fundamental primitive for hierarchical clustering and many other ML tasks, but this takes $\Omega(n^2)$ time to even approximate. We introduce a framework for metric MSTs that first (1) finds a forest of disconnected components using practical heuristics, and then (2) finds a small weight set of edges to connect disjoint components of the forest into a spanning tree. We prove that optimally solving the second step still takes $\Omega(n^2)$ time, but we provide a subquadratic 2.62-approximation algorithm. In the spirit of learning-augmented algorithms, we then show that if the forest found in step (1) overlaps with an optimal MST, we can approximate the original MST problem in subquadratic time, where the approximation factor depends on a measure of overlap. In practice, we find nearly optimal spanning trees for a wide range of metrics, while being orders of magnitude faster than exact algorithms.

Edge-Colored Clustering in Hypergraphs: Beyond Minimizing Unsatisfied Edges

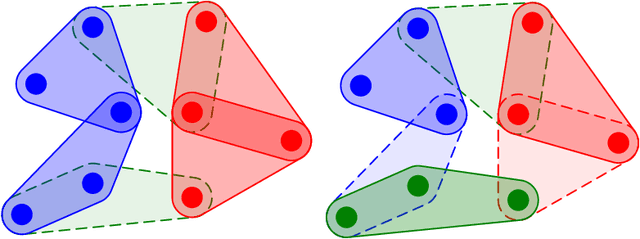
We consider a framework for clustering edge-colored hypergraphs, where the goal is to cluster (equivalently, to color) objects based on the primary type of multiway interactions they participate in. One well-studied objective is to color nodes to minimize the number of unsatisfied hyperedges -- those containing one or more nodes whose color does not match the hyperedge color. We motivate and present advances for several directions that extend beyond this minimization problem. We first provide new algorithms for maximizing satisfied edges, which is the same at optimality but is much more challenging to approximate, with all prior work restricted to graphs. We develop the first approximation algorithm for hypergraphs, and then refine it to improve the best-known approximation factor for graphs. We then introduce new objective functions that incorporate notions of balance and fairness, and provide new hardness results, approximations, and fixed-parameter tractability results.