Approximate Tree Completion and Learning-Augmented Algorithms for Metric Minimum Spanning Trees

Finding a minimum spanning tree (MST) for $n$ points in an arbitrary metric space is a fundamental primitive for hierarchical clustering and many other ML tasks, but this takes $\Omega(n^2)$ time to even approximate. We introduce a framework for metric MSTs that first (1) finds a forest of disconnected components using practical heuristics, and then (2) finds a small weight set of edges to connect disjoint components of the forest into a spanning tree. We prove that optimally solving the second step still takes $\Omega(n^2)$ time, but we provide a subquadratic 2.62-approximation algorithm. In the spirit of learning-augmented algorithms, we then show that if the forest found in step (1) overlaps with an optimal MST, we can approximate the original MST problem in subquadratic time, where the approximation factor depends on a measure of overlap. In practice, we find nearly optimal spanning trees for a wide range of metrics, while being orders of magnitude faster than exact algorithms.

Scaling Graph Clustering with Distributed Sketches

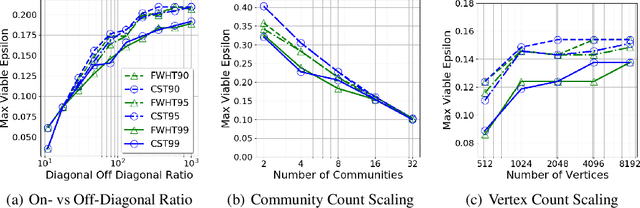
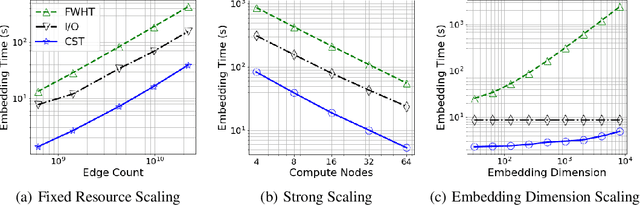
The unsupervised learning of community structure, in particular the partitioning vertices into clusters or communities, is a canonical and well-studied problem in exploratory graph analysis. However, like most graph analyses the introduction of immense scale presents challenges to traditional methods. Spectral clustering in distributed memory, for example, requires hundreds of expensive bulk-synchronous communication rounds to compute an embedding of vertices to a few eigenvectors of a graph associated matrix. Furthermore, the whole computation may need to be repeated if the underlying graph changes some low percentage of edge updates. We present a method inspired by spectral clustering where we instead use matrix sketches derived from random dimension-reducing projections. We show that our method produces embeddings that yield performant clustering results given a fully-dynamic stochastic block model stream using both the fast Johnson-Lindenstrauss and CountSketch transforms. We also discuss the effects of stochastic block model parameters upon the required dimensionality of the subsequent embeddings, and show how random projections could significantly improve the performance of graph clustering in distributed memory.

An Ensemble Framework for Detecting Community Changes in Dynamic Networks

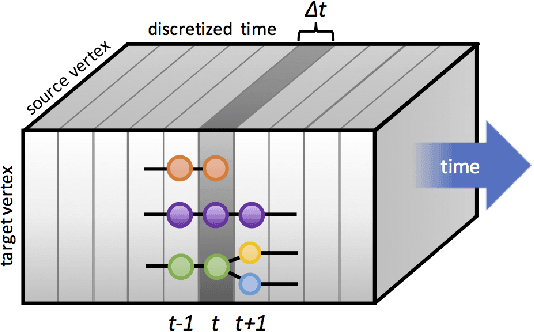
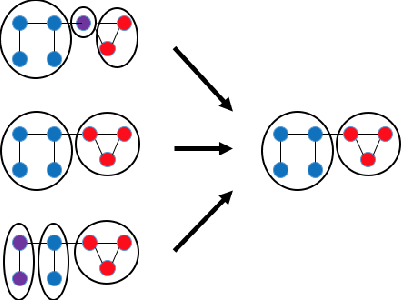
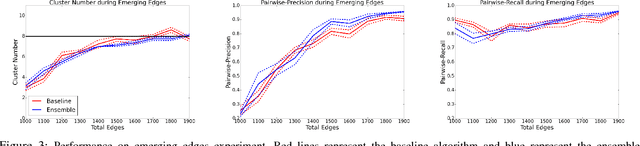
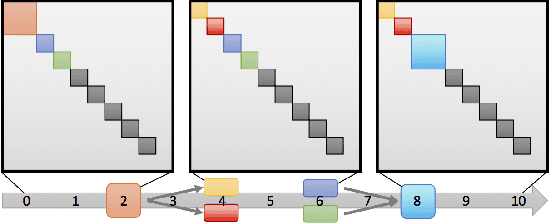
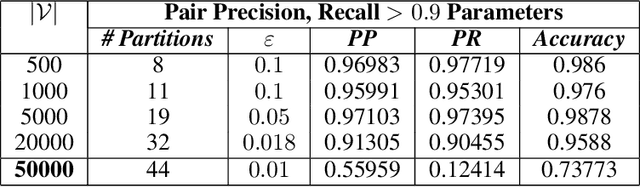
Dynamic networks, especially those representing social networks, undergo constant evolution of their community structure over time. Nodes can migrate between different communities, communities can split into multiple new communities, communities can merge together, etc. In order to represent dynamic networks with evolving communities it is essential to use a dynamic model rather than a static one. Here we use a dynamic stochastic block model where the underlying block model is different at different times. In order to represent the structural changes expressed by this dynamic model the network will be split into discrete time segments and a clustering algorithm will assign block memberships for each segment. In this paper we show that using an ensemble of clustering assignments accommodates for the variance in scalable clustering algorithms and produces superior results in terms of pairwise-precision and pairwise-recall. We also demonstrate that the dynamic clustering produced by the ensemble can be visualized as a flowchart which encapsulates the community evolution succinctly.