DYMOND: DYnamic MOtif-NoDes Network Generative Model

Motifs, which have been established as building blocks for network structure, move beyond pair-wise connections to capture longer-range correlations in connections and activity. In spite of this, there are few generative graph models that consider higher-order network structures and even fewer that focus on using motifs in models of dynamic graphs. Most existing generative models for temporal graphs strictly grow the networks via edge addition, and the models are evaluated using static graph structure metrics -- which do not adequately capture the temporal behavior of the network. To address these issues, in this work we propose DYnamic MOtif-NoDes (DYMOND) -- a generative model that considers (i) the dynamic changes in overall graph structure using temporal motif activity and (ii) the roles nodes play in motifs (e.g., one node plays the hub role in a wedge, while the remaining two act as spokes). We compare DYMOND to three dynamic graph generative model baselines on real-world networks and show that DYMOND performs better at generating graph structure and node behavior similar to the observed network. We also propose a new methodology to adapt graph structure metrics to better evaluate the temporal aspect of the network. These metrics take into account the changes in overall graph structure and the individual nodes' behavior over time.

Dynamic Vertex Replacement Grammars

Context-free graph grammars have shown a remarkable ability to model structures in real-world relational data. However, graph grammars lack the ability to capture time-changing phenomena since the left-to-right transitions of a production rule do not represent temporal change. In the present work, we describe dynamic vertex-replacement grammars (DyVeRG), which generalize vertex replacement grammars in the time domain by providing a formal framework for updating a learned graph grammar in accordance with modifications to its underlying data. We show that DyVeRG grammars can be learned from, and used to generate, real-world dynamic graphs faithfully while remaining human-interpretable. We also demonstrate their ability to forecast by computing dyvergence scores, a novel graph similarity measurement exposed by this framework.

An Ensemble Framework for Detecting Community Changes in Dynamic Networks

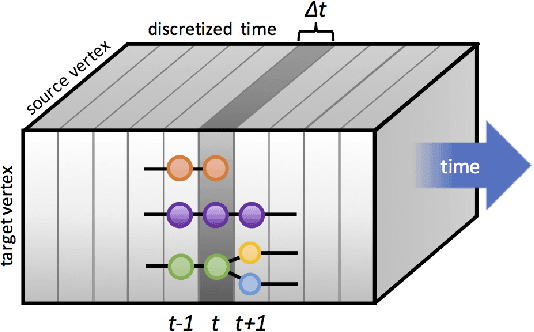
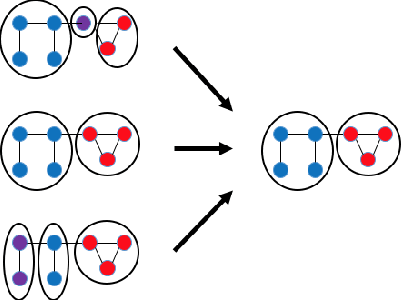
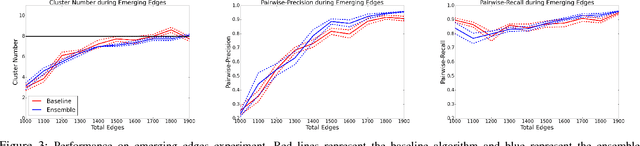
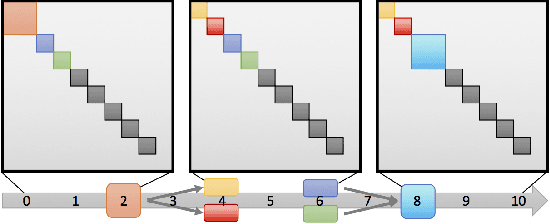
Dynamic networks, especially those representing social networks, undergo constant evolution of their community structure over time. Nodes can migrate between different communities, communities can split into multiple new communities, communities can merge together, etc. In order to represent dynamic networks with evolving communities it is essential to use a dynamic model rather than a static one. Here we use a dynamic stochastic block model where the underlying block model is different at different times. In order to represent the structural changes expressed by this dynamic model the network will be split into discrete time segments and a clustering algorithm will assign block memberships for each segment. In this paper we show that using an ensemble of clustering assignments accommodates for the variance in scalable clustering algorithms and produces superior results in terms of pairwise-precision and pairwise-recall. We also demonstrate that the dynamic clustering produced by the ensemble can be visualized as a flowchart which encapsulates the community evolution succinctly.

Size-Consistent Statistics for Anomaly Detection in Dynamic Networks

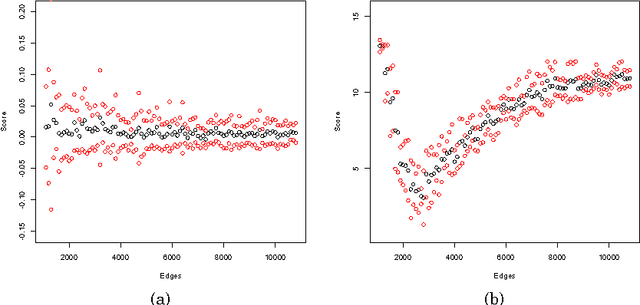
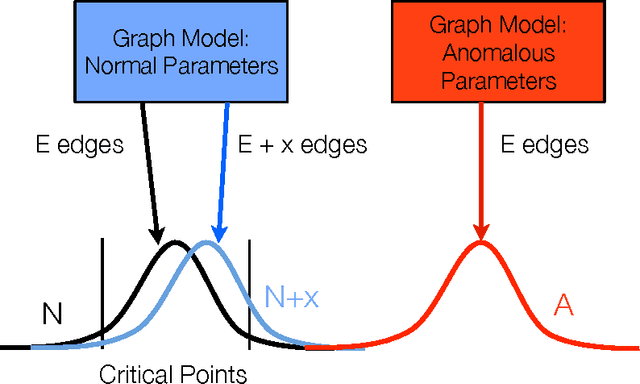
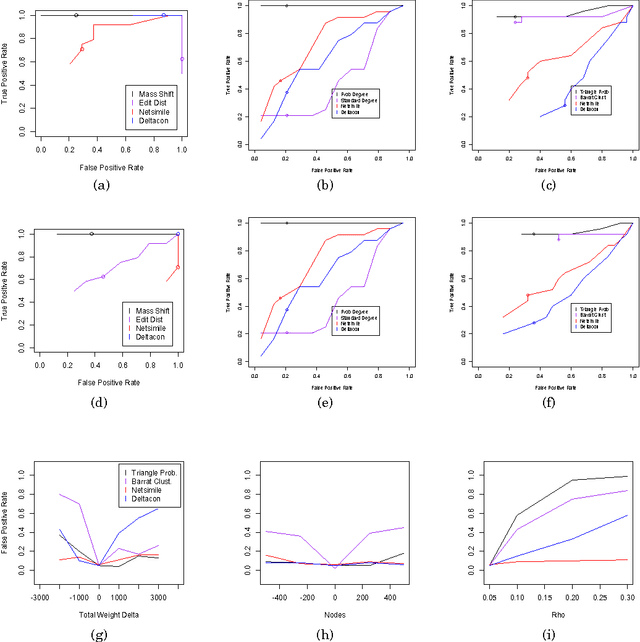
An important task in network analysis is the detection of anomalous events in a network time series. These events could merely be times of interest in the network timeline or they could be examples of malicious activity or network malfunction. Hypothesis testing using network statistics to summarize the behavior of the network provides a robust framework for the anomaly detection decision process. Unfortunately, choosing network statistics that are dependent on confounding factors like the total number of nodes or edges can lead to incorrect conclusions (e.g., false positives and false negatives). In this dissertation we describe the challenges that face anomaly detection in dynamic network streams regarding confounding factors. We also provide two solutions to avoiding error due to confounding factors: the first is a randomization testing method that controls for confounding factors, and the second is a set of size-consistent network statistics which avoid confounding due to the most common factors, edge count and node count.