Alec Dunton
Scaling Graph Clustering with Distributed Sketches
Jul 24, 2020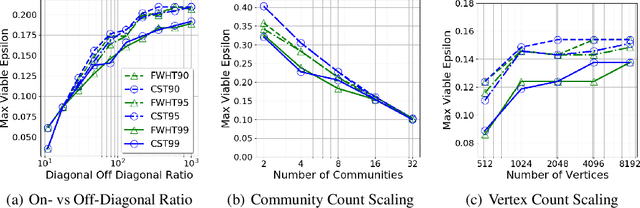
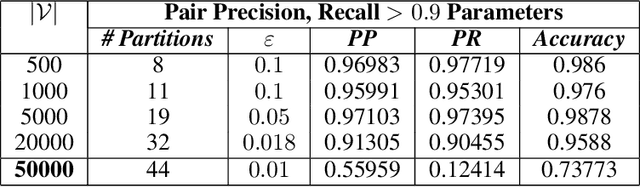
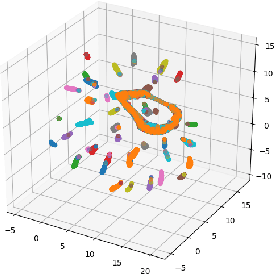
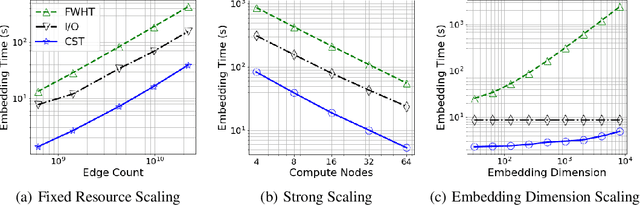
Abstract:The unsupervised learning of community structure, in particular the partitioning vertices into clusters or communities, is a canonical and well-studied problem in exploratory graph analysis. However, like most graph analyses the introduction of immense scale presents challenges to traditional methods. Spectral clustering in distributed memory, for example, requires hundreds of expensive bulk-synchronous communication rounds to compute an embedding of vertices to a few eigenvectors of a graph associated matrix. Furthermore, the whole computation may need to be repeated if the underlying graph changes some low percentage of edge updates. We present a method inspired by spectral clustering where we instead use matrix sketches derived from random dimension-reducing projections. We show that our method produces embeddings that yield performant clustering results given a fully-dynamic stochastic block model stream using both the fast Johnson-Lindenstrauss and CountSketch transforms. We also discuss the effects of stochastic block model parameters upon the required dimensionality of the subsequent embeddings, and show how random projections could significantly improve the performance of graph clustering in distributed memory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge