A nonlinear diffusion method for semi-supervised learning on hypergraphs

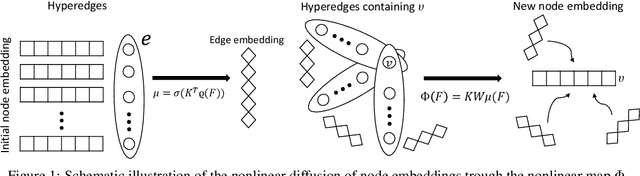
Hypergraphs are a common model for multiway relationships in data, and hypergraph semi-supervised learning is the problem of assigning labels to all nodes in a hypergraph, given labels on just a few nodes. Diffusions and label spreading are classical techniques for semi-supervised learning in the graph setting, and there are some standard ways to extend them to hypergraphs. However, these methods are linear models, and do not offer an obvious way of incorporating node features for making predictions. Here, we develop a nonlinear diffusion process on hypergraphs that spreads both features and labels following the hypergraph structure, which can be interpreted as a hypergraph equilibrium network. Even though the process is nonlinear, we show global convergence to a unique limiting point for a broad class of nonlinearities, which is the global optimum of a interpretable, regularized semi-supervised learning loss function. The limiting point serves as a node embedding from which we make predictions with a linear model. Our approach is much more accurate than several hypergraph neural networks, and also takes less time to train.

Nonlinear Higher-Order Label Spreading

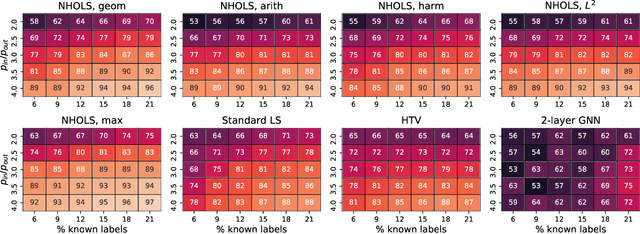
Label spreading is a general technique for semi-supervised learning with point cloud or network data, which can be interpreted as a diffusion of labels on a graph. While there are many variants of label spreading, nearly all of them are linear models, where the incoming information to a node is a weighted sum of information from neighboring nodes. Here, we add nonlinearity to label spreading through nonlinear functions of higher-order structure in the graph, namely triangles in the graph. For a broad class of nonlinear functions, we prove convergence of our nonlinear higher-order label spreading algorithm to the global solution of a constrained semi-supervised loss function. We demonstrate the efficiency and efficacy of our approach on a variety of point cloud and network datasets, where the nonlinear higher-order model compares favorably to classical label spreading, as well as hypergraph models and graph neural networks.