Statistical Models of Top-$k$ Partial Orders

In many contexts involving ranked preferences, agents submit partial orders over available alternatives. Statistical models often treat these as marginal in the space of total orders, but this approach overlooks information contained in the list length itself. In this work, we introduce and taxonomize approaches for jointly modeling distributions over top-$k$ partial orders and list lengths $k$, considering two classes of approaches: composite models that view a partial order as a truncation of a total order, and augmented ranking models that model the construction of the list as a sequence of choice decisions, including the decision to stop. For composite models, we consider three dependency structures for joint modeling of order and truncation length. For augmented ranking models, we consider different assumptions on how the stop-token choice is modeled. Using data consisting of partial rankings from San Francisco school choice and San Francisco ranked choice elections, we evaluate how well the models predict observed data and generate realistic synthetic datasets. We find that composite models, explicitly modeling length as a categorical variable, produce synthetic datasets with accurate length distributions, and an augmented model with position-dependent item utilities jointly models length and preferences in the training data best, as measured by negative log loss. Methods from this work have significant implications on the simulation and evaluation of real-world social systems that solicit ranked preferences.

Re-visiting Skip-Gram Negative Sampling: Dimension Regularization for More Efficient Dissimilarity Preservation in Graph Embeddings

A wide range of graph embedding objectives decompose into two components: one that attracts the embeddings of nodes that are perceived as similar, and another that repels embeddings of nodes that are perceived as dissimilar. Because real-world graphs are sparse and the number of dissimilar pairs grows quadratically with the number of nodes, Skip-Gram Negative Sampling (SGNS) has emerged as a popular and efficient repulsion approach. SGNS repels each node from a sample of dissimilar nodes, as opposed to all dissimilar nodes. In this work, we show that node-wise repulsion is, in aggregate, an approximate re-centering of the node embedding dimensions. Such dimension operations are much more scalable than node operations. The dimension approach, in addition to being more efficient, yields a simpler geometric interpretation of the repulsion. Our result extends findings from the self-supervised learning literature to the skip-gram model, establishing a connection between skip-gram node contrast and dimension regularization. We show that in the limit of large graphs, under mild regularity conditions, the original node repulsion objective converges to optimization with dimension regularization. We use this observation to propose an algorithm augmentation framework that speeds up any existing algorithm, supervised or unsupervised, using SGNS. The framework prioritizes node attraction and replaces SGNS with dimension regularization. We instantiate this generic framework for LINE and node2vec and show that the augmented algorithms preserve downstream performance while dramatically increasing efficiency.

Inferring Dynamic Networks from Marginals with Iterative Proportional Fitting

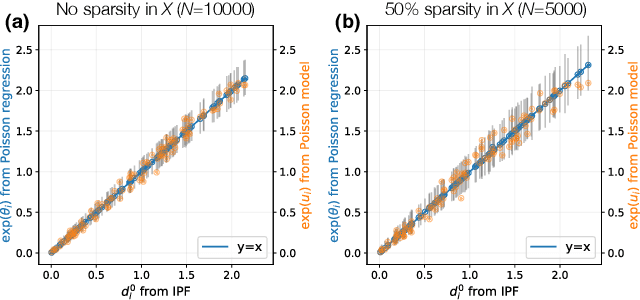
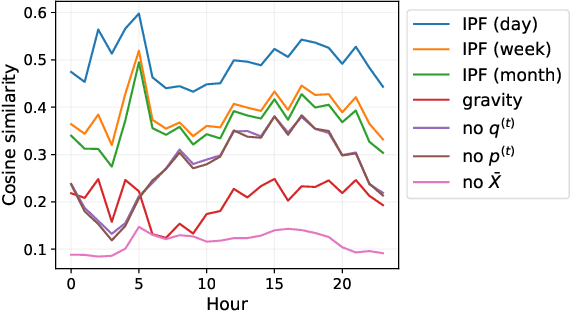
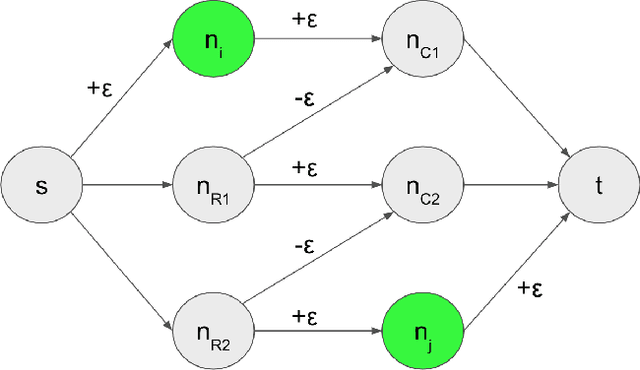
A common network inference problem, arising from real-world data constraints, is how to infer a dynamic network from its time-aggregated adjacency matrix and time-varying marginals (i.e., row and column sums). Prior approaches to this problem have repurposed the classic iterative proportional fitting (IPF) procedure, also known as Sinkhorn's algorithm, with promising empirical results. However, the statistical foundation for using IPF has not been well understood: under what settings does IPF provide principled estimation of a dynamic network from its marginals, and how well does it estimate the network? In this work, we establish such a setting, by identifying a generative network model whose maximum likelihood estimates are recovered by IPF. Our model both reveals implicit assumptions on the use of IPF in such settings and enables new analyses, such as structure-dependent error bounds on IPF's parameter estimates. When IPF fails to converge on sparse network data, we introduce a principled algorithm that guarantees IPF converges under minimal changes to the network structure. Finally, we conduct experiments with synthetic and real-world data, which demonstrate the practical value of our theoretical and algorithmic contributions.

Learning Rich Rankings

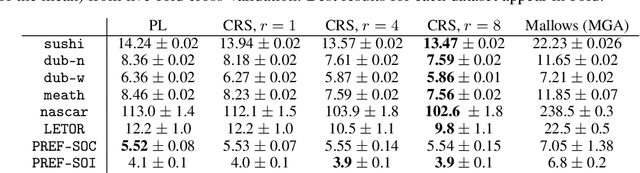
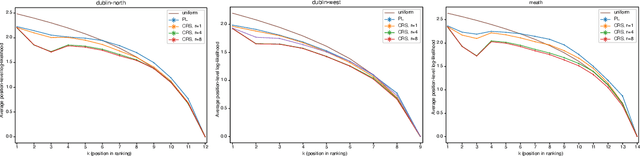
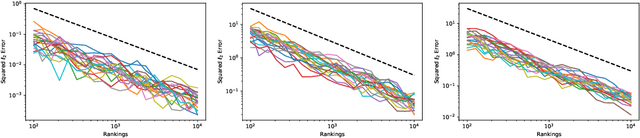
Although the foundations of ranking are well established, the ranking literature has primarily been focused on simple, unimodal models, e.g. the Mallows and Plackett-Luce models, that define distributions centered around a single total ordering. Explicit mixture models have provided some tools for modelling multimodal ranking data, though learning such models from data is often difficult. In this work, we contribute a contextual repeated selection (CRS) model that leverages recent advances in choice modeling to bring a natural multimodality and richness to the rankings space. We provide rigorous theoretical guarantees for maximum likelihood estimation under the model through structure-dependent tail risk and expected risk bounds. As a by-product, we also furnish the first tight bounds on the expected risk of maximum likelihood estimators for the multinomial logit (MNL) choice model and the Plackett-Luce (PL) ranking model, as well as the first tail risk bound on the PL ranking model. The CRS model significantly outperforms existing methods for modeling real world ranking data in a variety of settings, from racing to rank choice voting.

On Sinkhorn's Algorithm and Choice Modeling

For a broad class of choice and ranking models based on Luce's choice axiom, including the Bradley--Terry--Luce and Plackett--Luce models, we show that the associated maximum likelihood estimation problems are equivalent to a classic matrix balancing problem with target row and column sums. This perspective opens doors between two seemingly unrelated research areas, and allows us to unify existing algorithms in the choice modeling literature as special instances or analogs of Sinkhorn's celebrated algorithm for matrix balancing. We draw inspirations from these connections and resolve important open problems on the study of Sinkhorn's algorithm. We first prove the global linear convergence of Sinkhorn's algorithm for non-negative matrices whenever finite solutions to the matrix balancing problem exist. We characterize this global rate of convergence in terms of the algebraic connectivity of the bipartite graph constructed from data. Next, we also derive the sharp asymptotic rate of linear convergence, which generalizes a classic result of Knight (2008), but with a more explicit analysis that exploits an intrinsic orthogonality structure. To our knowledge, these are the first quantitative linear convergence results for Sinkhorn's algorithm for general non-negative matrices and positive marginals. The connections we establish in this paper between matrix balancing and choice modeling could help motivate further transmission of ideas and interesting results in both directions.

Counterfactual Evaluation of Peer-Review Assignment Policies

Peer review assignment algorithms aim to match research papers to suitable expert reviewers, working to maximize the quality of the resulting reviews. A key challenge in designing effective assignment policies is evaluating how changes to the assignment algorithm map to changes in review quality. In this work, we leverage recently proposed policies that introduce randomness in peer-review assignment--in order to mitigate fraud--as a valuable opportunity to evaluate counterfactual assignment policies. Specifically, we exploit how such randomized assignments provide a positive probability of observing the reviews of many assignment policies of interest. To address challenges in applying standard off-policy evaluation methods, such as violations of positivity, we introduce novel methods for partial identification based on monotonicity and Lipschitz smoothness assumptions for the mapping between reviewer-paper covariates and outcomes. We apply our methods to peer-review data from two computer science venues: the TPDP'21 workshop (95 papers and 35 reviewers) and the AAAI'22 conference (8,450 papers and 3,145 reviewers). We consider estimates of (i) the effect on review quality when changing weights in the assignment algorithm, e.g., weighting reviewers' bids vs. textual similarity (between the review's past papers and the submission), and (ii) the "cost of randomization", capturing the difference in expected quality between the perturbed and unperturbed optimal match. We find that placing higher weight on text similarity results in higher review quality and that introducing randomization in the reviewer-paper assignment only marginally reduces the review quality. Our methods for partial identification may be of independent interest, while our off-policy approach can likely find use evaluating a broad class of algorithmic matching systems.

Choice Set Confounding in Discrete Choice

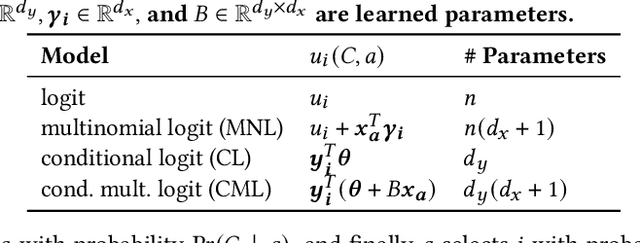
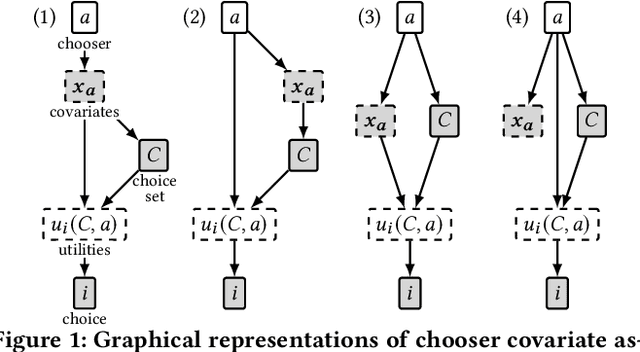
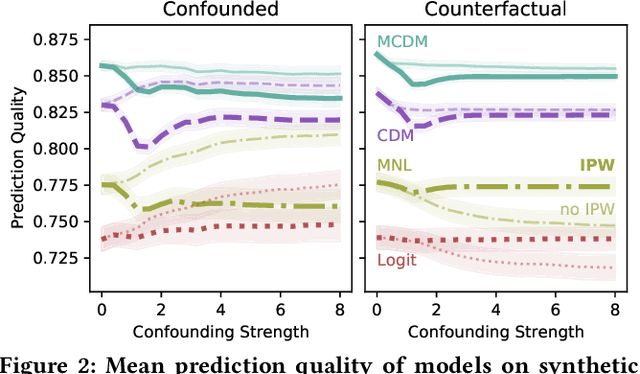
Standard methods in preference learning involve estimating the parameters of discrete choice models from data of selections (choices) made by individuals from a discrete set of alternatives (the choice set). While there are many models for individual preferences, existing learning methods overlook how choice set assignment affects the data. Often, the choice set itself is influenced by an individual's preferences; for instance, a consumer choosing a product from an online retailer is often presented with options from a recommender system that depend on information about the consumer's preferences. Ignoring these assignment mechanisms can mislead choice models into making biased estimates of preferences, a phenomenon that we call choice set confounding; we demonstrate the presence of such confounding in widely-used choice datasets. To address this issue, we adapt methods from causal inference to the discrete choice setting. We use covariates of the chooser for inverse probability weighting and/or regression controls, accurately recovering individual preferences in the presence of choice set confounding under certain assumptions. When such covariates are unavailable or inadequate, we develop methods that take advantage of structured choice set assignment to improve prediction. We demonstrate the effectiveness of our methods on real-world choice data, showing, for example, that accounting for choice set confounding makes choices observed in hotel booking and commute transportation more consistent with rational utility-maximization.

Fundamental Limits of Testing the Independence of Irrelevant Alternatives in Discrete Choice

The Multinomial Logit (MNL) model and the axiom it satisfies, the Independence of Irrelevant Alternatives (IIA), are together the most widely used tools of discrete choice. The MNL model serves as the workhorse model for a variety of fields, but is also widely criticized, with a large body of experimental literature claiming to document real-world settings where IIA fails to hold. Statistical tests of IIA as a modelling assumption have been the subject of many practical tests focusing on specific deviations from IIA over the past several decades, but the formal size properties of hypothesis testing IIA are still not well understood. In this work we replace some of the ambiguity in this literature with rigorous pessimism, demonstrating that any general test for IIA with low worst-case error would require a number of samples exponential in the number of alternatives of the choice problem. A major benefit of our analysis over previous work is that it lies entirely in the finite-sample domain, a feature crucial to understanding the behavior of tests in the common data-poor settings of discrete choice. Our lower bounds are structure-dependent, and as a potential cause for optimism, we find that if one restricts the test of IIA to violations that can occur in a specific collection of choice sets (e.g., pairs), one obtains structure-dependent lower bounds that are much less pessimistic. Our analysis of this testing problem is unorthodox in being highly combinatorial, counting Eulerian orientations of cycle decompositions of a particular bipartite graph constructed from a data set of choices. By identifying fundamental relationships between the comparison structure of a given testing problem and its sample efficiency, we hope these relationships will help lay the groundwork for a rigorous rethinking of the IIA testing problem as well as other testing problems in discrete choice.

Discovering Context Effects from Raw Choice Data

Many applications in preference learning assume that decisions come from the maximization of a stable utility function. Yet a large experimental literature shows that individual choices and judgements can be affected by "irrelevant" aspects of the context in which they are made. An important class of such contexts is the composition of the choice set. In this work, our goal is to discover such choice set effects from raw choice data. We introduce an extension of the Multinomial Logit (MNL) model, called the context dependent random utility model (CDM), which allows for a particular class of choice set effects. We show that the CDM can be thought of as a second-order approximation to a general choice system, can be inferred optimally using maximum likelihood and, importantly, is easily interpretable. We apply the CDM to both real and simulated choice data to perform principled exploratory analyses for the presence of choice set effects.

Choosing to Rank

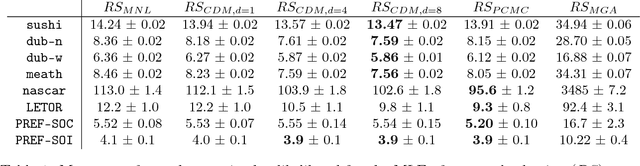
Ranking data arises in a wide variety of application areas, generated both by complex algorithms and by human subjects, but remains difficult to model, learn from, and predict. Particularly when generated by humans, ranking datasets often feature multiple modes, intransitive aggregate preferences, or incomplete rankings, but popular probabilistic models such as the Plackett-Luce and Mallows models are too rigid to capture such complexities. In this work, we frame ranking as a sequence of discrete choices and then leverage recent advances in discrete choice modeling to build flexible and tractable models of ranking data. The basic building block of our connection between ranking and choice is the idea of repeated selection, first used to build the Plackett-Luce ranking model from the multinomial logit (MNL) choice model by repeatedly applying the choice model to a dwindling set of alternatives. We derive conditions under which repeated selection can be applied to other choice models to build new ranking models, addressing specific subtleties with modeling mixed-length top-k rankings as repeated selection. We translate several choice axioms through our framework, providing structure to our ranking models inherited from the underlying choice models. To train models from data, we transform ranking data into choice data and employ standard techniques for training choice models. We find that our ranking models provide higher out-of-sample likelihood when compared to Plackett-Luce and Mallows models on a broad collection of ranking tasks including food preferences, ranked-choice elections, car racing, and search engine relevance ranking data.