Choosing to Rank

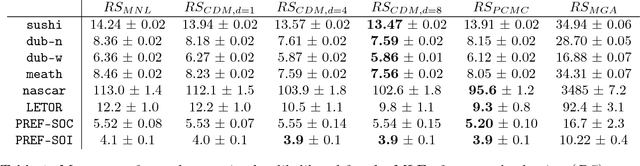
Ranking data arises in a wide variety of application areas, generated both by complex algorithms and by human subjects, but remains difficult to model, learn from, and predict. Particularly when generated by humans, ranking datasets often feature multiple modes, intransitive aggregate preferences, or incomplete rankings, but popular probabilistic models such as the Plackett-Luce and Mallows models are too rigid to capture such complexities. In this work, we frame ranking as a sequence of discrete choices and then leverage recent advances in discrete choice modeling to build flexible and tractable models of ranking data. The basic building block of our connection between ranking and choice is the idea of repeated selection, first used to build the Plackett-Luce ranking model from the multinomial logit (MNL) choice model by repeatedly applying the choice model to a dwindling set of alternatives. We derive conditions under which repeated selection can be applied to other choice models to build new ranking models, addressing specific subtleties with modeling mixed-length top-k rankings as repeated selection. We translate several choice axioms through our framework, providing structure to our ranking models inherited from the underlying choice models. To train models from data, we transform ranking data into choice data and employ standard techniques for training choice models. We find that our ranking models provide higher out-of-sample likelihood when compared to Plackett-Luce and Mallows models on a broad collection of ranking tasks including food preferences, ranked-choice elections, car racing, and search engine relevance ranking data.