Learning Rich Rankings

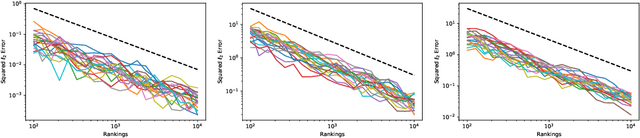
Although the foundations of ranking are well established, the ranking literature has primarily been focused on simple, unimodal models, e.g. the Mallows and Plackett-Luce models, that define distributions centered around a single total ordering. Explicit mixture models have provided some tools for modelling multimodal ranking data, though learning such models from data is often difficult. In this work, we contribute a contextual repeated selection (CRS) model that leverages recent advances in choice modeling to bring a natural multimodality and richness to the rankings space. We provide rigorous theoretical guarantees for maximum likelihood estimation under the model through structure-dependent tail risk and expected risk bounds. As a by-product, we also furnish the first tight bounds on the expected risk of maximum likelihood estimators for the multinomial logit (MNL) choice model and the Plackett-Luce (PL) ranking model, as well as the first tail risk bound on the PL ranking model. The CRS model significantly outperforms existing methods for modeling real world ranking data in a variety of settings, from racing to rank choice voting.

MiCRO: Multi-interest Candidate Retrieval Online

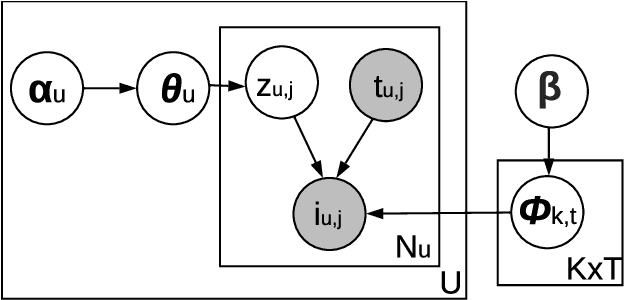
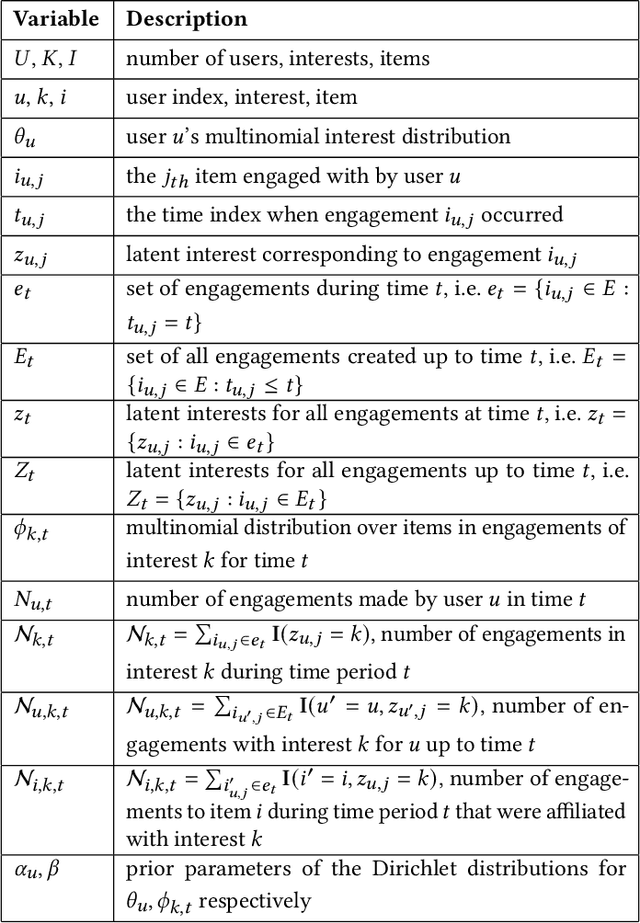
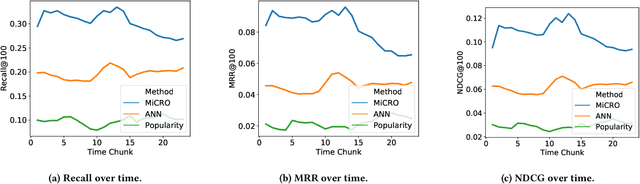
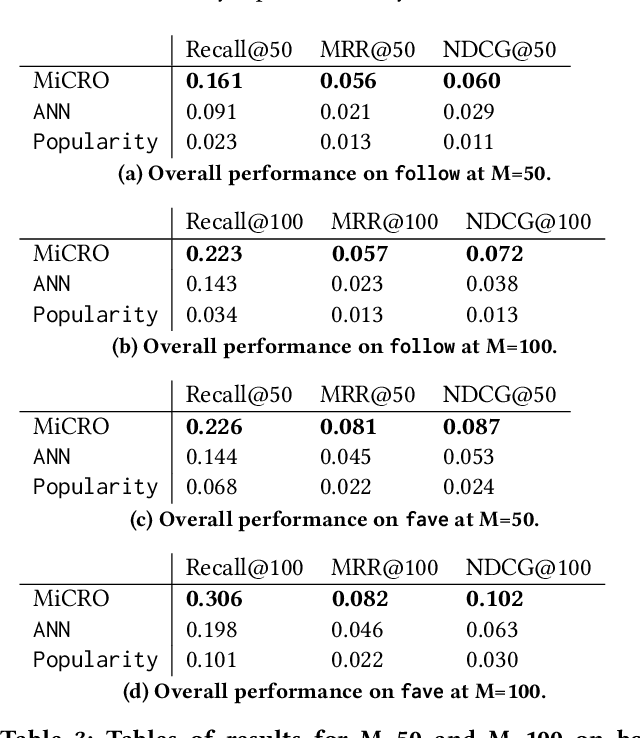
Providing personalized recommendations in an environment where items exhibit ephemerality and temporal relevancy (e.g. in social media) presents a few unique challenges: (1) inductively understanding ephemeral appeal for items in a setting where new items are created frequently, (2) adapting to trends within engagement patterns where items may undergo temporal shifts in relevance, (3) accurately modeling user preferences over this item space where users may express multiple interests. In this work we introduce MiCRO, a generative statistical framework that models multi-interest user preferences and temporal multi-interest item representations. Our framework is specifically formulated to adapt to both new items and temporal patterns of engagement. MiCRO demonstrates strong empirical performance on candidate retrieval experiments performed on two large scale user-item datasets: (1) an open-source temporal dataset of (User, User) follow interactions and (2) a temporal dataset of (User, Tweet) favorite interactions which we will open-source as an additional contribution to the community.

Choosing to Rank

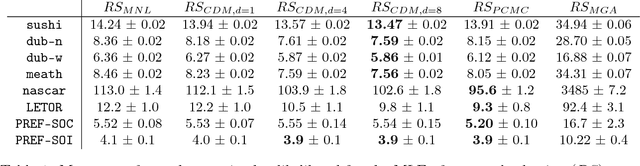
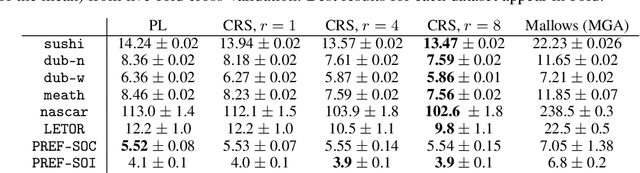
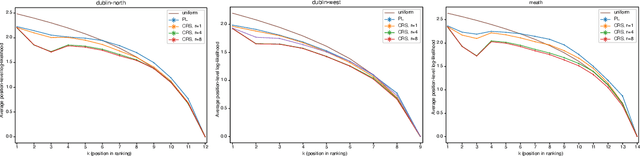
Ranking data arises in a wide variety of application areas, generated both by complex algorithms and by human subjects, but remains difficult to model, learn from, and predict. Particularly when generated by humans, ranking datasets often feature multiple modes, intransitive aggregate preferences, or incomplete rankings, but popular probabilistic models such as the Plackett-Luce and Mallows models are too rigid to capture such complexities. In this work, we frame ranking as a sequence of discrete choices and then leverage recent advances in discrete choice modeling to build flexible and tractable models of ranking data. The basic building block of our connection between ranking and choice is the idea of repeated selection, first used to build the Plackett-Luce ranking model from the multinomial logit (MNL) choice model by repeatedly applying the choice model to a dwindling set of alternatives. We derive conditions under which repeated selection can be applied to other choice models to build new ranking models, addressing specific subtleties with modeling mixed-length top-k rankings as repeated selection. We translate several choice axioms through our framework, providing structure to our ranking models inherited from the underlying choice models. To train models from data, we transform ranking data into choice data and employ standard techniques for training choice models. We find that our ranking models provide higher out-of-sample likelihood when compared to Plackett-Luce and Mallows models on a broad collection of ranking tasks including food preferences, ranked-choice elections, car racing, and search engine relevance ranking data.

Improving pairwise comparison models using Empirical Bayes shrinkage

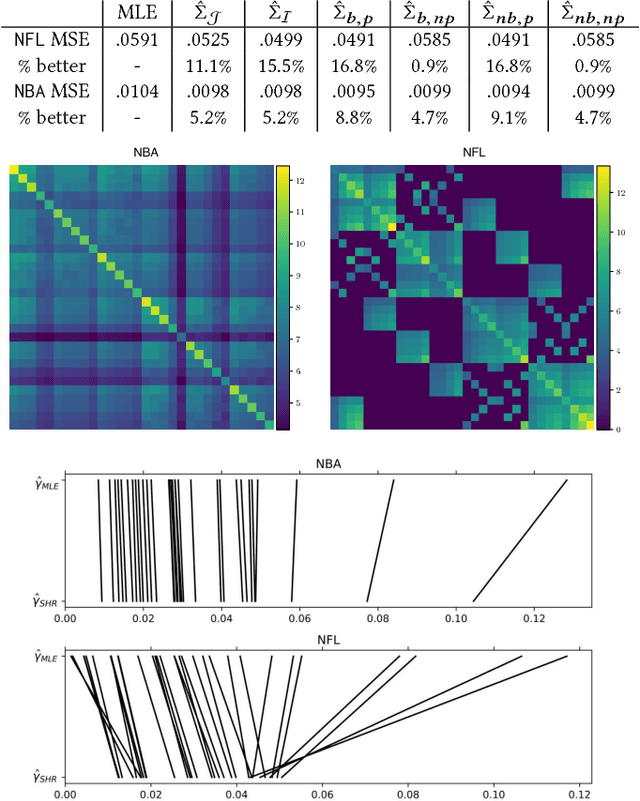
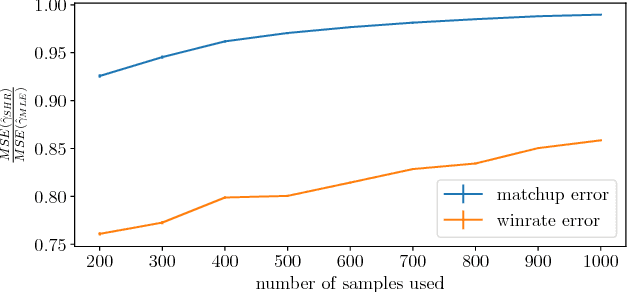
Comparison data arises in many important contexts, e.g. shopping, web clicks, or sports competitions. Typically we are given a dataset of comparisons and wish to train a model to make predictions about the outcome of unseen comparisons. In many cases available datasets have relatively few comparisons (e.g. there are only so many NFL games per year) or efficiency is important (e.g. we want to quickly estimate the relative appeal of a product). In such settings it is well known that shrinkage estimators outperform maximum likelihood estimators. A complicating matter is that standard comparison models such as the conditional multinomial logit model are only models of conditional outcomes (who wins) and not of comparisons themselves (who competes). As such, different models of the comparison process lead to different shrinkage estimators. In this work we derive a collection of methods for estimating the pairwise uncertainty of pairwise predictions based on different assumptions about the comparison process. These uncertainty estimates allow us both to examine model uncertainty as well as perform Empirical Bayes shrinkage estimation of the model parameters. We demonstrate that our shrunk estimators outperform standard maximum likelihood methods on real comparison data from online comparison surveys as well as from several sports contexts.

Pairwise Choice Markov Chains

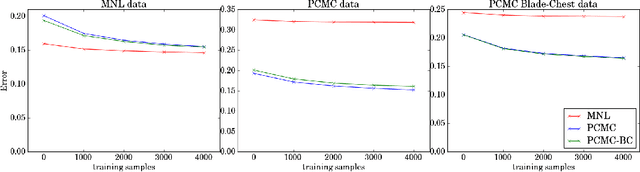
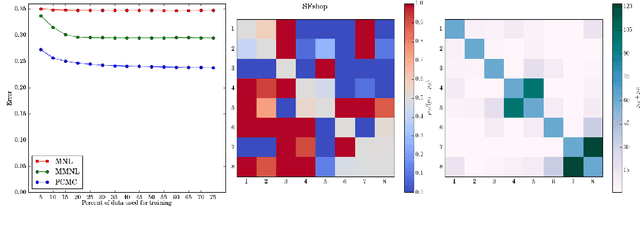
As datasets capturing human choices grow in richness and scale---particularly in online domains---there is an increasing need for choice models that escape traditional choice-theoretic axioms such as regularity, stochastic transitivity, and Luce's choice axiom. In this work we introduce the Pairwise Choice Markov Chain (PCMC) model of discrete choice, an inferentially tractable model that does not assume any of the above axioms while still satisfying the foundational axiom of uniform expansion, a considerably weaker assumption than Luce's choice axiom. We show that the PCMC model significantly outperforms the Multinomial Logit (MNL) model in prediction tasks on both synthetic and empirical datasets known to exhibit violations of Luce's axiom. Our analysis also synthesizes several recent observations connecting the Multinomial Logit model and Markov chains; the PCMC model retains the Multinomial Logit model as a special case.