Improving pairwise comparison models using Empirical Bayes shrinkage
Paper and Code
Jul 24, 2018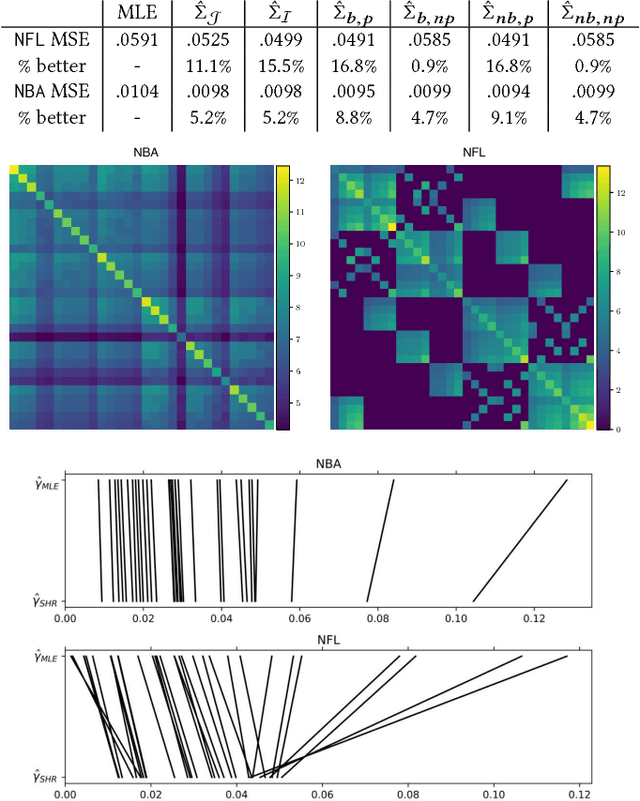
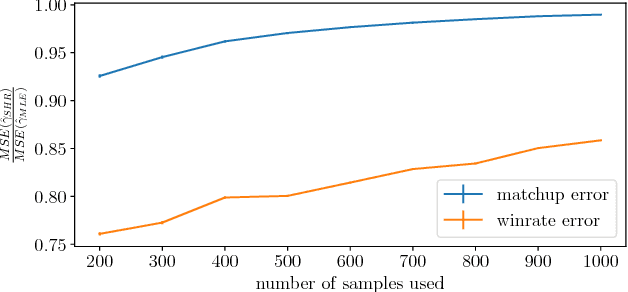

Comparison data arises in many important contexts, e.g. shopping, web clicks, or sports competitions. Typically we are given a dataset of comparisons and wish to train a model to make predictions about the outcome of unseen comparisons. In many cases available datasets have relatively few comparisons (e.g. there are only so many NFL games per year) or efficiency is important (e.g. we want to quickly estimate the relative appeal of a product). In such settings it is well known that shrinkage estimators outperform maximum likelihood estimators. A complicating matter is that standard comparison models such as the conditional multinomial logit model are only models of conditional outcomes (who wins) and not of comparisons themselves (who competes). As such, different models of the comparison process lead to different shrinkage estimators. In this work we derive a collection of methods for estimating the pairwise uncertainty of pairwise predictions based on different assumptions about the comparison process. These uncertainty estimates allow us both to examine model uncertainty as well as perform Empirical Bayes shrinkage estimation of the model parameters. We demonstrate that our shrunk estimators outperform standard maximum likelihood methods on real comparison data from online comparison surveys as well as from several sports contexts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge