Inferring Dynamic Networks from Marginals with Iterative Proportional Fitting
Paper and Code
Feb 28, 2024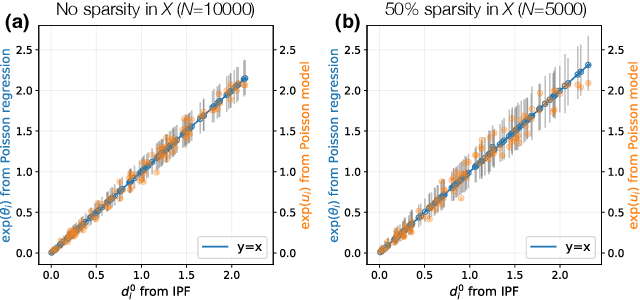
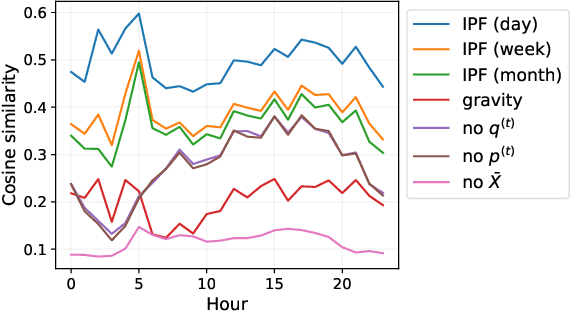

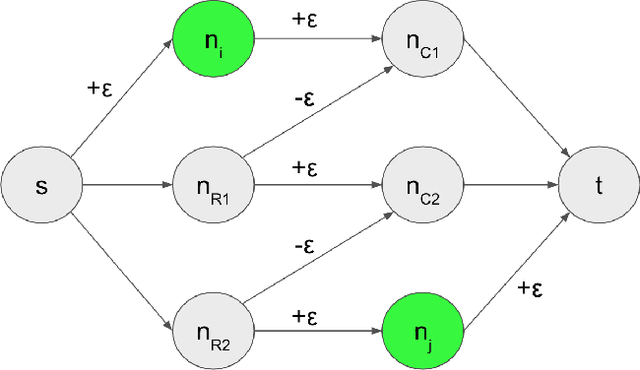
A common network inference problem, arising from real-world data constraints, is how to infer a dynamic network from its time-aggregated adjacency matrix and time-varying marginals (i.e., row and column sums). Prior approaches to this problem have repurposed the classic iterative proportional fitting (IPF) procedure, also known as Sinkhorn's algorithm, with promising empirical results. However, the statistical foundation for using IPF has not been well understood: under what settings does IPF provide principled estimation of a dynamic network from its marginals, and how well does it estimate the network? In this work, we establish such a setting, by identifying a generative network model whose maximum likelihood estimates are recovered by IPF. Our model both reveals implicit assumptions on the use of IPF in such settings and enables new analyses, such as structure-dependent error bounds on IPF's parameter estimates. When IPF fails to converge on sparse network data, we introduce a principled algorithm that guarantees IPF converges under minimal changes to the network structure. Finally, we conduct experiments with synthetic and real-world data, which demonstrate the practical value of our theoretical and algorithmic contributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge