Distributionally Robust Instrumental Variables Estimation

Instrumental variables (IV) estimation is a fundamental method in econometrics and statistics for estimating causal effects in the presence of unobserved confounding. However, challenges such as untestable model assumptions and poor finite sample properties have undermined its reliability in practice. Viewing common issues in IV estimation as distributional uncertainties, we propose DRIVE, a distributionally robust framework of the classical IV estimation method. When the ambiguity set is based on a Wasserstein distance, DRIVE minimizes a square root ridge regularized variant of the two stage least squares (TSLS) objective. We develop a novel asymptotic theory for this regularized regression estimator based on the square root ridge, showing that it achieves consistency without requiring the regularization parameter to vanish. This result follows from a fundamental property of the square root ridge, which we call ``delayed shrinkage''. This novel property, which also holds for a class of generalized method of moments (GMM) estimators, ensures that the estimator is robust to distributional uncertainties that persist in large samples. We further derive the asymptotic distribution of Wasserstein DRIVE and propose data-driven procedures to select the regularization parameter based on theoretical results. Simulation studies confirm the superior finite sample performance of Wasserstein DRIVE. Thanks to its regularization and robustness properties, Wasserstein DRIVE could be preferable in practice, particularly when the practitioner is uncertain about model assumptions or distributional shifts in data.

Inferring Dynamic Networks from Marginals with Iterative Proportional Fitting

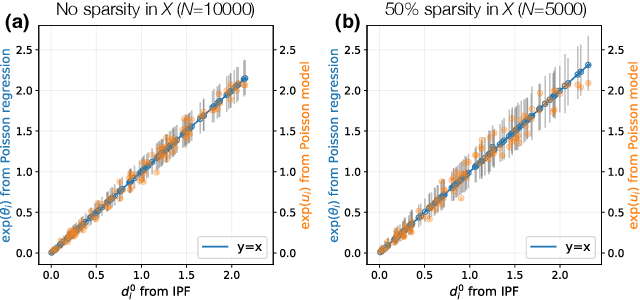
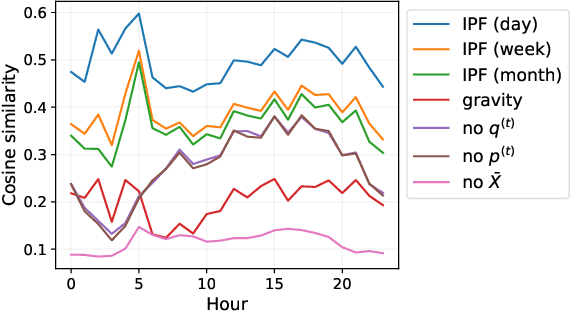
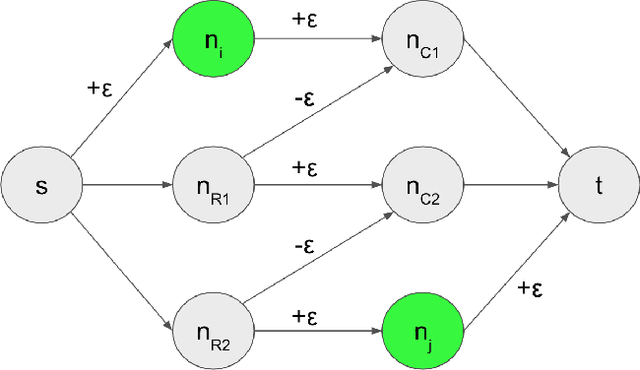
A common network inference problem, arising from real-world data constraints, is how to infer a dynamic network from its time-aggregated adjacency matrix and time-varying marginals (i.e., row and column sums). Prior approaches to this problem have repurposed the classic iterative proportional fitting (IPF) procedure, also known as Sinkhorn's algorithm, with promising empirical results. However, the statistical foundation for using IPF has not been well understood: under what settings does IPF provide principled estimation of a dynamic network from its marginals, and how well does it estimate the network? In this work, we establish such a setting, by identifying a generative network model whose maximum likelihood estimates are recovered by IPF. Our model both reveals implicit assumptions on the use of IPF in such settings and enables new analyses, such as structure-dependent error bounds on IPF's parameter estimates. When IPF fails to converge on sparse network data, we introduce a principled algorithm that guarantees IPF converges under minimal changes to the network structure. Finally, we conduct experiments with synthetic and real-world data, which demonstrate the practical value of our theoretical and algorithmic contributions.

On Sinkhorn's Algorithm and Choice Modeling

For a broad class of choice and ranking models based on Luce's choice axiom, including the Bradley--Terry--Luce and Plackett--Luce models, we show that the associated maximum likelihood estimation problems are equivalent to a classic matrix balancing problem with target row and column sums. This perspective opens doors between two seemingly unrelated research areas, and allows us to unify existing algorithms in the choice modeling literature as special instances or analogs of Sinkhorn's celebrated algorithm for matrix balancing. We draw inspirations from these connections and resolve important open problems on the study of Sinkhorn's algorithm. We first prove the global linear convergence of Sinkhorn's algorithm for non-negative matrices whenever finite solutions to the matrix balancing problem exist. We characterize this global rate of convergence in terms of the algebraic connectivity of the bipartite graph constructed from data. Next, we also derive the sharp asymptotic rate of linear convergence, which generalizes a classic result of Knight (2008), but with a more explicit analysis that exploits an intrinsic orthogonality structure. To our knowledge, these are the first quantitative linear convergence results for Sinkhorn's algorithm for general non-negative matrices and positive marginals. The connections we establish in this paper between matrix balancing and choice modeling could help motivate further transmission of ideas and interesting results in both directions.

Optimal Diagonal Preconditioning: Theory and Practice

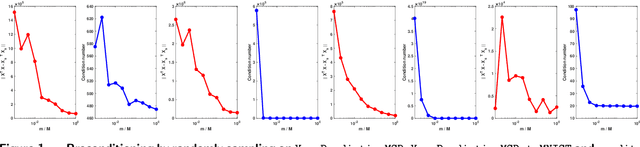
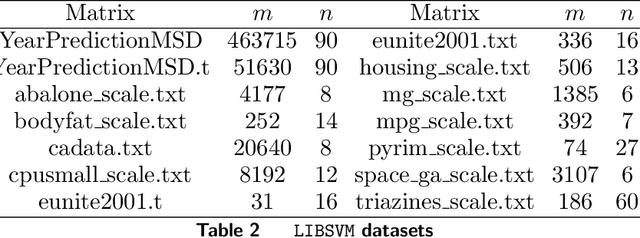
Preconditioning has been a staple technique in optimization and machine learning. It often reduces the condition number of the matrix it is applied to, thereby speeding up convergence of optimization algorithms. Although there are many popular preconditioning techniques in practice, most lack theoretical guarantees for reductions in condition number. In this paper, we study the problem of optimal diagonal preconditioning to achieve maximal reduction in the condition number of any full-rank matrix by scaling its rows or columns separately or simultaneously. We first reformulate the problem as a quasi-convex problem and provide a baseline bisection algorithm that is easy to implement in practice, where each iteration consists of an SDP feasibility problem. Then we propose a polynomial time potential reduction algorithm with $O(\log(\frac{1}{\epsilon}))$ iteration complexity, where each iteration consists of a Newton update based on the Nesterov-Todd direction. Our algorithm is based on a formulation of the problem which is a generalized version of the Von Neumann optimal growth problem. Next, we specialize to one-sided optimal diagonal preconditioning problems, and demonstrate that they can be formulated as standard dual SDP problems, to which we apply efficient customized solvers and study the empirical performance of our optimal diagonal preconditioners. Our extensive experiments on large matrices demonstrate the practical appeal of optimal diagonal preconditioners at reducing condition numbers compared to heuristics-based preconditioners.

Federated Learning's Blessing: FedAvg has Linear Speedup

Federated learning (FL) learns a model jointly from a set of participating devices without sharing each other's privately held data. The characteristics of non-iid data across the network, low device participation, and the mandate that data remain private bring challenges in understanding the convergence of FL algorithms, particularly in regards to how convergence scales with the number of participating devices. In this paper, we focus on Federated Averaging (FedAvg)--the most widely used and effective FL algorithm in use today--and provide a comprehensive study of its convergence rate. Although FedAvg has recently been studied by an emerging line of literature, it remains open as to how FedAvg's convergence scales with the number of participating devices in the FL setting--a crucial question whose answer would shed light on the performance of FedAvg in large FL systems. We fill this gap by establishing convergence guarantees for FedAvg under three classes of problems: strongly convex smooth, convex smooth, and overparameterized strongly convex smooth problems. We show that FedAvg enjoys linear speedup in each case, although with different convergence rates. For each class, we also characterize the corresponding convergence rates for the Nesterov accelerated FedAvg algorithm in the FL setting: to the best of our knowledge, these are the first linear speedup guarantees for FedAvg when Nesterov acceleration is used. To accelerate FedAvg, we also design a new momentum-based FL algorithm that further improves the convergence rate in overparameterized linear regression problems. Empirical studies of the algorithms in various settings have supported our theoretical results.

Diagonal Preconditioning: Theory and Algorithms

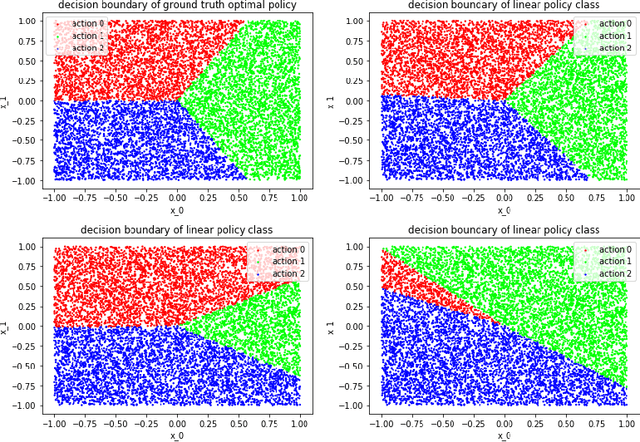
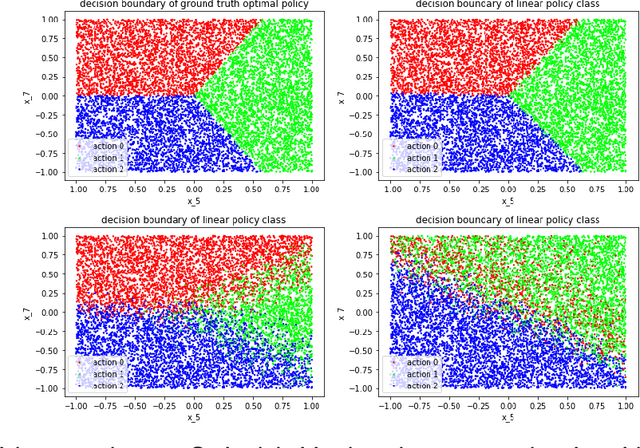
Diagonal preconditioning has been a staple technique in optimization and machine learning. It often reduces the condition number of the design or Hessian matrix it is applied to, thereby speeding up convergence. However, rigorous analyses of how well various diagonal preconditioning procedures improve the condition number of the preconditioned matrix and how that translates into improvements in optimization are rare. In this paper, we first provide an analysis of a popular diagonal preconditioning technique based on column standard deviation and its effect on the condition number using random matrix theory. Then we identify a class of design matrices whose condition numbers can be reduced significantly by this procedure. We then study the problem of optimal diagonal preconditioning to improve the condition number of any full-rank matrix and provide a bisection algorithm and a potential reduction algorithm with $O(\log(\frac{1}{\epsilon}))$ iteration complexity, where each iteration consists of an SDP feasibility problem and a Newton update using the Nesterov-Todd direction, respectively. Finally, we extend the optimal diagonal preconditioning algorithm to an adaptive setting and compare its empirical performance at reducing the condition number and speeding up convergence for regression and classification problems with that of another adaptive preconditioning technique, namely batch normalization, that is essential in training machine learning models.