Oliver Hinder
Dj
The Sample Complexity of Parameter-Free Stochastic Convex Optimization
Jun 12, 2025Abstract:We study the sample complexity of stochastic convex optimization when problem parameters, e.g., the distance to optimality, are unknown. We pursue two strategies. First, we develop a reliable model selection method that avoids overfitting the validation set. This method allows us to generically tune the learning rate of stochastic optimization methods to match the optimal known-parameter sample complexity up to $\log\log$ factors. Second, we develop a regularization-based method that is specialized to the case that only the distance to optimality is unknown. This method provides perfect adaptability to unknown distance to optimality, demonstrating a separation between the sample and computational complexity of parameter-free stochastic convex optimization. Combining these two methods allows us to simultaneously adapt to multiple problem structures. Experiments performing few-shot learning on CIFAR-10 by fine-tuning CLIP models and prompt engineering Gemini to count shapes indicate that our reliable model selection method can help mitigate overfitting to small validation sets.
Accelerated Parameter-Free Stochastic Optimization
Mar 31, 2024Abstract:We propose a method that achieves near-optimal rates for smooth stochastic convex optimization and requires essentially no prior knowledge of problem parameters. This improves on prior work which requires knowing at least the initial distance to optimality d0. Our method, U-DoG, combines UniXGrad (Kavis et al., 2019) and DoG (Ivgi et al., 2023) with novel iterate stabilization techniques. It requires only loose bounds on d0 and the noise magnitude, provides high probability guarantees under sub-Gaussian noise, and is also near-optimal in the non-smooth case. Our experiments show consistent, strong performance on convex problems and mixed results on neural network training.
The Price of Adaptivity in Stochastic Convex Optimization
Feb 16, 2024Abstract:We prove impossibility results for adaptivity in non-smooth stochastic convex optimization. Given a set of problem parameters we wish to adapt to, we define a "price of adaptivity" (PoA) that, roughly speaking, measures the multiplicative increase in suboptimality due to uncertainty in these parameters. When the initial distance to the optimum is unknown but a gradient norm bound is known, we show that the PoA is at least logarithmic for expected suboptimality, and double-logarithmic for median suboptimality. When there is uncertainty in both distance and gradient norm, we show that the PoA must be polynomial in the level of uncertainty. Our lower bounds nearly match existing upper bounds, and establish that there is no parameter-free lunch.
Datasets and Benchmarks for Nanophotonic Structure and Parametric Design Simulations
Oct 29, 2023Abstract:Nanophotonic structures have versatile applications including solar cells, anti-reflective coatings, electromagnetic interference shielding, optical filters, and light emitting diodes. To design and understand these nanophotonic structures, electrodynamic simulations are essential. These simulations enable us to model electromagnetic fields over time and calculate optical properties. In this work, we introduce frameworks and benchmarks to evaluate nanophotonic structures in the context of parametric structure design problems. The benchmarks are instrumental in assessing the performance of optimization algorithms and identifying an optimal structure based on target optical properties. Moreover, we explore the impact of varying grid sizes in electrodynamic simulations, shedding light on how evaluation fidelity can be strategically leveraged in enhancing structure designs.
DoG is SGD's Best Friend: A Parameter-Free Dynamic Step Size Schedule
Feb 08, 2023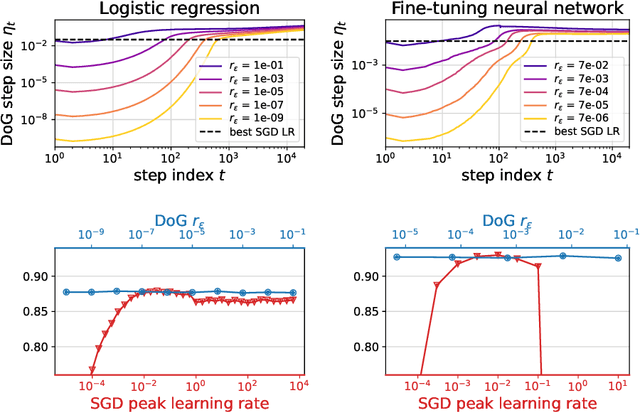
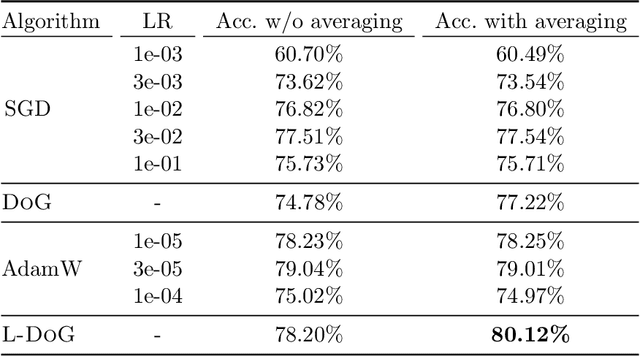

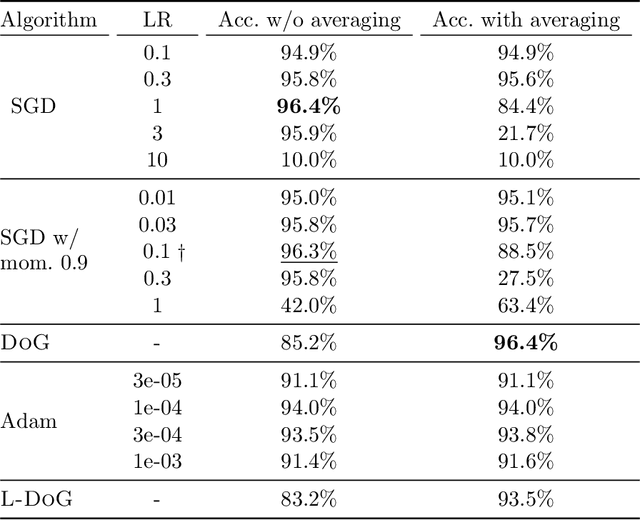
Abstract:We propose a tuning-free dynamic SGD step size formula, which we call Distance over Gradients (DoG). The DoG step sizes depend on simple empirical quantities (distance from the initial point and norms of gradients) and have no ``learning rate'' parameter. Theoretically, we show that a slight variation of the DoG formula enjoys strong parameter-free convergence guarantees for stochastic convex optimization assuming only \emph{locally bounded} stochastic gradients. Empirically, we consider a broad range of vision and language transfer learning tasks, and show that DoG's performance is close to that of SGD with tuned learning rate. We also propose a per-layer variant of DoG that generally outperforms tuned SGD, approaching the performance of tuned Adam.
Optimal Diagonal Preconditioning: Theory and Practice
Sep 02, 2022
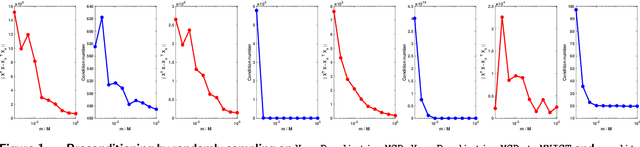
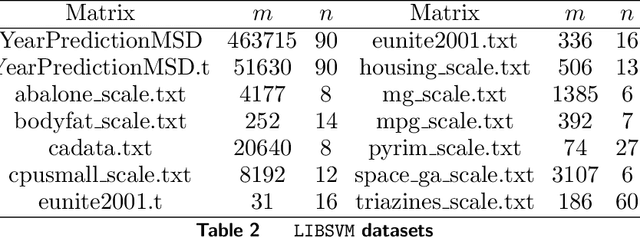

Abstract:Preconditioning has been a staple technique in optimization and machine learning. It often reduces the condition number of the matrix it is applied to, thereby speeding up convergence of optimization algorithms. Although there are many popular preconditioning techniques in practice, most lack theoretical guarantees for reductions in condition number. In this paper, we study the problem of optimal diagonal preconditioning to achieve maximal reduction in the condition number of any full-rank matrix by scaling its rows or columns separately or simultaneously. We first reformulate the problem as a quasi-convex problem and provide a baseline bisection algorithm that is easy to implement in practice, where each iteration consists of an SDP feasibility problem. Then we propose a polynomial time potential reduction algorithm with $O(\log(\frac{1}{\epsilon}))$ iteration complexity, where each iteration consists of a Newton update based on the Nesterov-Todd direction. Our algorithm is based on a formulation of the problem which is a generalized version of the Von Neumann optimal growth problem. Next, we specialize to one-sided optimal diagonal preconditioning problems, and demonstrate that they can be formulated as standard dual SDP problems, to which we apply efficient customized solvers and study the empirical performance of our optimal diagonal preconditioners. Our extensive experiments on large matrices demonstrate the practical appeal of optimal diagonal preconditioners at reducing condition numbers compared to heuristics-based preconditioners.
Making SGD Parameter-Free
May 04, 2022Abstract:We develop an algorithm for parameter-free stochastic convex optimization (SCO) whose rate of convergence is only a double-logarithmic factor larger than the optimal rate for the corresponding known-parameter setting. In contrast, the best previously known rates for parameter-free SCO are based on online parameter-free regret bounds, which contain unavoidable excess logarithmic terms compared to their known-parameter counterparts. Our algorithm is conceptually simple, has high-probability guarantees, and is also partially adaptive to unknown gradient norms, smoothness, and strong convexity. At the heart of our results is a novel parameter-free certificate for SGD step size choice, and a time-uniform concentration result that assumes no a-priori bounds on SGD iterates.
An efficient nonconvex reformulation of stagewise convex optimization problems
Oct 27, 2020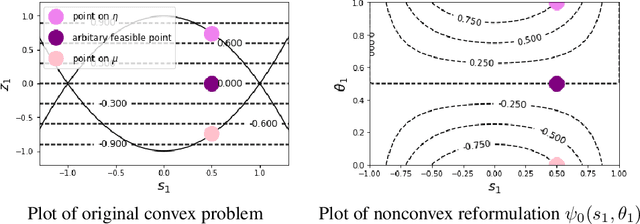
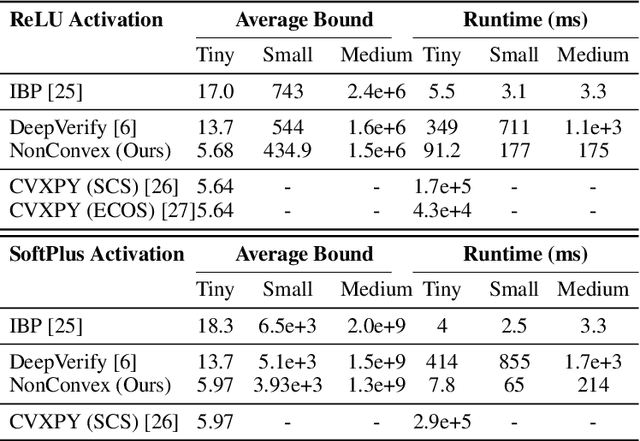
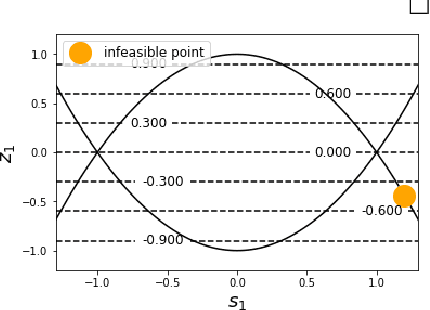
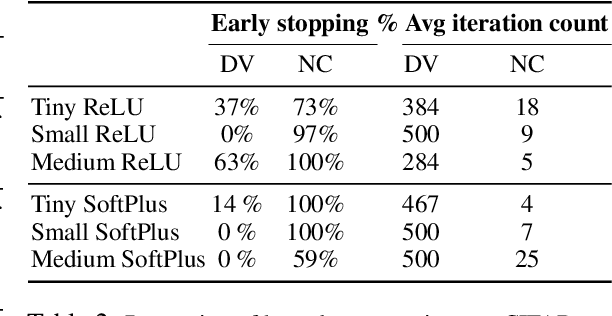
Abstract:Convex optimization problems with staged structure appear in several contexts, including optimal control, verification of deep neural networks, and isotonic regression. Off-the-shelf solvers can solve these problems but may scale poorly. We develop a nonconvex reformulation designed to exploit this staged structure. Our reformulation has only simple bound constraints, enabling solution via projected gradient methods and their accelerated variants. The method automatically generates a sequence of primal and dual feasible solutions to the original convex problem, making optimality certification easy. We establish theoretical properties of the nonconvex formulation, showing that it is (almost) free of spurious local minima and has the same global optimum as the convex problem. We modify PGD to avoid spurious local minimizers so it always converges to the global minimizer. For neural network verification, our approach obtains small duality gaps in only a few gradient steps. Consequently, it can quickly solve large-scale verification problems faster than both off-the-shelf and specialized solvers.
Near-Optimal Methods for Minimizing Star-Convex Functions and Beyond
Jun 27, 2019
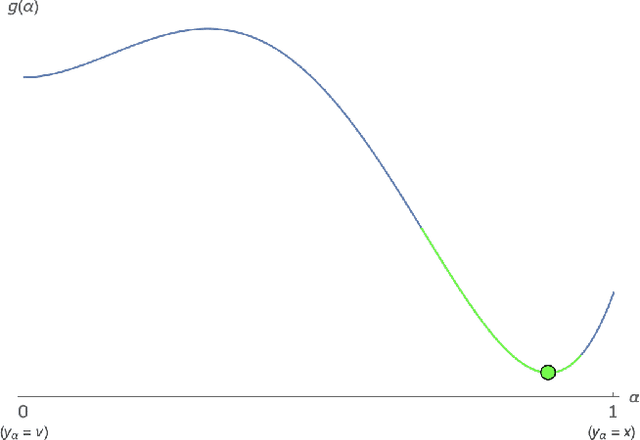
Abstract:In this paper, we provide near-optimal accelerated first-order methods for minimizing a broad class of smooth nonconvex functions that are strictly unimodal on all lines through a minimizer. This function class, which we call the class of smooth quasar-convex functions, is parameterized by a constant $\gamma \in (0,1]$, where $\gamma = 1$ encompasses the classes of smooth convex and star-convex functions, and smaller values of $\gamma$ indicate that the function can be "more nonconvex." We develop a variant of accelerated gradient descent that computes an $\epsilon$-approximate minimizer of a smooth $\gamma$-quasar-convex function with at most $O(\gamma^{-1} \epsilon^{-1/2} \log(\gamma^{-1} \epsilon^{-1}))$ total function and gradient evaluations. We also derive a lower bound of $\Omega(\gamma^{-1} \epsilon^{-1/2})$ on the number of gradient evaluations required by any deterministic first-order method in the worst case, showing that, up to a logarithmic factor, no deterministic first-order algorithm can improve upon ours.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge