Model Fusion through Bayesian Optimization in Language Model Fine-Tuning

Fine-tuning pre-trained models for downstream tasks is a widely adopted technique known for its adaptability and reliability across various domains. Despite its conceptual simplicity, fine-tuning entails several troublesome engineering choices, such as selecting hyperparameters and determining checkpoints from an optimization trajectory. To tackle the difficulty of choosing the best model, one effective solution is model fusion, which combines multiple models in a parameter space. However, we observe a large discrepancy between loss and metric landscapes during the fine-tuning of pre-trained language models. Building on this observation, we introduce a novel model fusion technique that optimizes both the desired metric and loss through multi-objective Bayesian optimization. In addition, to effectively select hyperparameters, we establish a two-stage procedure by integrating Bayesian optimization processes into our framework. Experiments across various downstream tasks show considerable performance improvements using our Bayesian optimization-guided method.

Exploiting Preferences in Loss Functions for Sequential Recommendation via Weak Transitivity

A choice of optimization objective is immensely pivotal in the design of a recommender system as it affects the general modeling process of a user's intent from previous interactions. Existing approaches mainly adhere to three categories of loss functions: pairwise, pointwise, and setwise loss functions. Despite their effectiveness, a critical and common drawback of such objectives is viewing the next observed item as a unique positive while considering all remaining items equally negative. Such a binary label assignment is generally limited to assuring a higher recommendation score of the positive item, neglecting potential structures induced by varying preferences between other unobserved items. To alleviate this issue, we propose a novel method that extends original objectives to explicitly leverage the different levels of preferences as relative orders between their scores. Finally, we demonstrate the superior performance of our method compared to baseline objectives.

Noise-Adaptive Confidence Sets for Linear Bandits and Application to Bayesian Optimization

Adapting to a priori unknown noise level is a very important but challenging problem in sequential decision-making as efficient exploration typically requires knowledge of the noise level, which is often loosely specified. We report significant progress in addressing this issue in linear bandits in two respects. First, we propose a novel confidence set that is `semi-adaptive' to the unknown sub-Gaussian parameter $\sigma_*^2$ in the sense that the (normalized) confidence width scales with $\sqrt{d\sigma_*^2 + \sigma_0^2}$ where $d$ is the dimension and $\sigma_0^2$ is the specified sub-Gaussian parameter (known) that can be much larger than $\sigma_*^2$. This is a significant improvement over $\sqrt{d\sigma_0^2}$ of the standard confidence set of Abbasi-Yadkori et al. (2011), especially when $d$ is large. We show that this leads to an improved regret bound in linear bandits. Second, for bounded rewards, we propose a novel variance-adaptive confidence set that has a much improved numerical performance upon prior art. We then apply this confidence set to develop, as we claim, the first practical variance-adaptive linear bandit algorithm via an optimistic approach, which is enabled by our novel regret analysis technique. Both of our confidence sets rely critically on `regret equality' from online learning. Our empirical evaluation in Bayesian optimization tasks shows that our algorithms demonstrate better or comparable performance compared to existing methods.

Beyond Regrets: Geometric Metrics for Bayesian Optimization

Bayesian optimization is a principled optimization strategy for a black-box objective function. It shows its effectiveness in a wide variety of real-world applications such as scientific discovery and experimental design. In general, the performance of Bayesian optimization is assessed by regret-based metrics such as instantaneous, simple, and cumulative regrets. These metrics only rely on function evaluations, so that they do not consider geometric relationships between query points and global solutions, or query points themselves. Notably, they cannot discriminate if multiple global solutions are successfully found. Moreover, they do not evaluate Bayesian optimization's abilities to exploit and explore a search space given. To tackle these issues, we propose four new geometric metrics, i.e., precision, recall, average degree, and average distance. These metrics allow us to compare Bayesian optimization algorithms considering the geometry of both query points and global optima, or query points. However, they are accompanied by an extra parameter, which needs to be carefully determined. We therefore devise the parameter-free forms of the respective metrics by integrating out the additional parameter. Finally, we empirically validate that our proposed metrics can provide more convincing interpretation and understanding of Bayesian optimization algorithms from distinct perspectives, compared to the conventional metrics.

Generative Neural Fields by Mixtures of Neural Implicit Functions

We propose a novel approach to learning the generative neural fields represented by linear combinations of implicit basis networks. Our algorithm learns basis networks in the form of implicit neural representations and their coefficients in a latent space by either conducting meta-learning or adopting auto-decoding paradigms. The proposed method easily enlarges the capacity of generative neural fields by increasing the number of basis networks while maintaining the size of a network for inference to be small through their weighted model averaging. Consequently, sampling instances using the model is efficient in terms of latency and memory footprint. Moreover, we customize denoising diffusion probabilistic model for a target task to sample latent mixture coefficients, which allows our final model to generate unseen data effectively. Experiments show that our approach achieves competitive generation performance on diverse benchmarks for images, voxel data, and NeRF scenes without sophisticated designs for specific modalities and domains.

Datasets and Benchmarks for Nanophotonic Structure and Parametric Design Simulations

Nanophotonic structures have versatile applications including solar cells, anti-reflective coatings, electromagnetic interference shielding, optical filters, and light emitting diodes. To design and understand these nanophotonic structures, electrodynamic simulations are essential. These simulations enable us to model electromagnetic fields over time and calculate optical properties. In this work, we introduce frameworks and benchmarks to evaluate nanophotonic structures in the context of parametric structure design problems. The benchmarks are instrumental in assessing the performance of optimization algorithms and identifying an optimal structure based on target optical properties. Moreover, we explore the impact of varying grid sizes in electrodynamic simulations, shedding light on how evaluation fidelity can be strategically leveraged in enhancing structure designs.

Generalized Neural Sorting Networks with Error-Free Differentiable Swap Functions

Sorting is a fundamental operation of all computer systems, having been a long-standing significant research topic. Beyond the problem formulation of traditional sorting algorithms, we consider sorting problems for more abstract yet expressive inputs, e.g., multi-digit images and image fragments, through a neural sorting network. To learn a mapping from a high-dimensional input to an ordinal variable, the differentiability of sorting networks needs to be guaranteed. In this paper we define a softening error by a differentiable swap function, and develop an error-free swap function that holds non-decreasing and differentiability conditions. Furthermore, a permutation-equivariant Transformer network with multi-head attention is adopted to capture dependency between given inputs and also leverage its model capacity with self-attention. Experiments on diverse sorting benchmarks show that our methods perform better than or comparable to baseline methods.

Density Ratio Estimation-based Bayesian Optimization with Semi-Supervised Learning

Bayesian optimization has attracted huge attention from diverse research areas in science and engineering, since it is capable of finding a global optimum of an expensive-to-evaluate black-box function efficiently. In general, a probabilistic regression model, e.g., Gaussian processes, random forests, and Bayesian neural networks, is widely used as a surrogate function to model an explicit distribution over function evaluations given an input to estimate and a training dataset. Beyond the probabilistic regression-based Bayesian optimization, density ratio estimation-based Bayesian optimization has been suggested in order to estimate a density ratio of the groups relatively close and relatively far to a global optimum. Developing this line of research further, a supervised classifier can be employed to estimate a class probability for the two groups instead of a density ratio. However, the supervised classifiers used in this strategy tend to be overconfident for a global solution candidate. To solve this overconfidence problem, we propose density ratio estimation-based Bayesian optimization with semi-supervised learning. Finally, we demonstrate the experimental results of our methods and several baseline methods in two distinct scenarios with unlabeled point sampling and a fixed-size pool.

Sequential Brick Assembly with Efficient Constraint Satisfaction

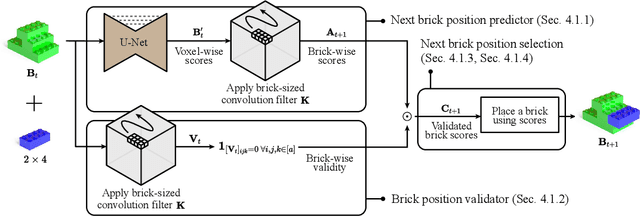
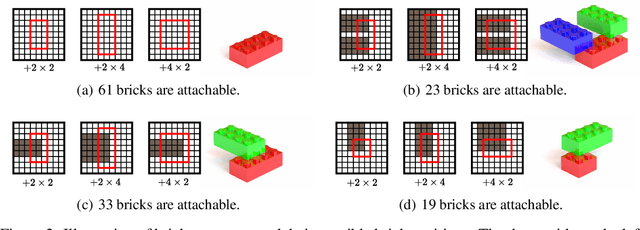
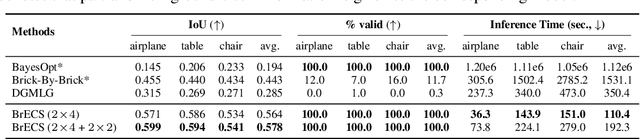
We address the problem of generating a sequence of LEGO brick assembly with high-fidelity structures, satisfying physical constraints between bricks. The assembly problem is challenging since the number of possible structures increases exponentially with the number of available bricks, complicating the physical constraints to satisfy across bricks. To tackle this problem, our method performs a brick structure assessment to predict the next brick position and its confidence by employing a U-shaped sparse 3D convolutional network. The convolution filter efficiently validates physical constraints in a parallelizable and scalable manner, allowing to process of different brick types. To generate a novel structure, we devise a sampling strategy to determine the next brick position by considering attachable positions under physical constraints. Instead of using handcrafted brick assembly datasets, our model is trained with a large number of 3D objects that allow to create a new high-fidelity structure. We demonstrate that our method successfully generates diverse brick structures while handling two different brick types and outperforms existing methods based on Bayesian optimization, graph generative model, and reinforcement learning, all of which are limited to a single brick type.

Learning to Assemble Geometric Shapes

Assembling parts into an object is a combinatorial problem that arises in a variety of contexts in the real world and involves numerous applications in science and engineering. Previous related work tackles limited cases with identical unit parts or jigsaw-style parts of textured shapes, which greatly mitigate combinatorial challenges of the problem. In this work, we introduce the more challenging problem of shape assembly, which involves textureless fragments of arbitrary shapes with indistinctive junctions, and then propose a learning-based approach to solving it. We demonstrate the effectiveness on shape assembly tasks with various scenarios, including the ones with abnormal fragments (e.g., missing and distorted), the different number of fragments, and different rotation discretization.