Dimension Agnostic Neural Processes

Meta-learning aims to train models that can generalize to new tasks with limited labeled data by extracting shared features across diverse task datasets. Additionally, it accounts for prediction uncertainty during both training and evaluation, a concept known as uncertainty-aware meta-learning. Neural Process(NP) is a well-known uncertainty-aware meta-learning method that constructs implicit stochastic processes using parametric neural networks, enabling rapid adaptation to new tasks. However, existing NP methods face challenges in accommodating diverse input dimensions and learned features, limiting their broad applicability across regression tasks. To address these limitations and advance the utility of NP models as general regressors, we introduce Dimension Agnostic Neural Processes(DANP). DANP incorporates Dimension Aggregator Block(DAB) to transform input features into a fixed-dimensional space, enhancing the model's ability to handle diverse datasets. Furthermore, leveraging the Transformer architecture and latent encoding layers, DANP learns a wider range of features that are generalizable across various tasks. Through comprehensive experimentation on various synthetic and practical regression tasks, we empirically show that DANP outperforms previous NP variations, showcasing its effectiveness in overcoming the limitations of traditional NP models and its potential for broader applicability in diverse regression scenarios.

Variational Bayesian Pseudo-Coreset

The success of deep learning requires large datasets and extensive training, which can create significant computational challenges. To address these challenges, pseudo-coresets, small learnable datasets that mimic the entire data, have been proposed. Bayesian Neural Networks, which offer predictive uncertainty and probabilistic interpretation for deep neural networks, also face issues with large-scale datasets due to their high-dimensional parameter space. Prior works on Bayesian Pseudo-Coresets (BPC) attempt to reduce the computational load for computing weight posterior distribution by a small number of pseudo-coresets but suffer from memory inefficiency during BPC training and sub-optimal results. To overcome these limitations, we propose Variational Bayesian Pseudo-Coreset (VBPC), a novel approach that utilizes variational inference to efficiently approximate the posterior distribution, reducing memory usage and computational costs while improving performance across benchmark datasets.

Model Fusion through Bayesian Optimization in Language Model Fine-Tuning

Fine-tuning pre-trained models for downstream tasks is a widely adopted technique known for its adaptability and reliability across various domains. Despite its conceptual simplicity, fine-tuning entails several troublesome engineering choices, such as selecting hyperparameters and determining checkpoints from an optimization trajectory. To tackle the difficulty of choosing the best model, one effective solution is model fusion, which combines multiple models in a parameter space. However, we observe a large discrepancy between loss and metric landscapes during the fine-tuning of pre-trained language models. Building on this observation, we introduce a novel model fusion technique that optimizes both the desired metric and loss through multi-objective Bayesian optimization. In addition, to effectively select hyperparameters, we establish a two-stage procedure by integrating Bayesian optimization processes into our framework. Experiments across various downstream tasks show considerable performance improvements using our Bayesian optimization-guided method.

Amortized Control of Continuous State Space Feynman-Kac Model for Irregular Time Series

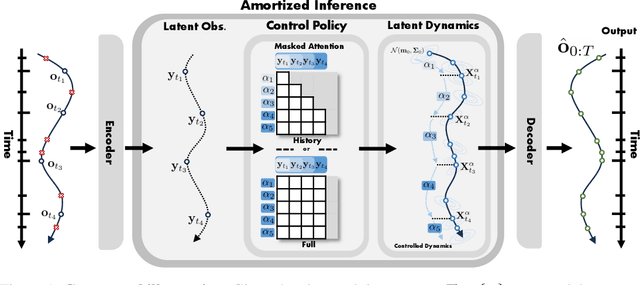
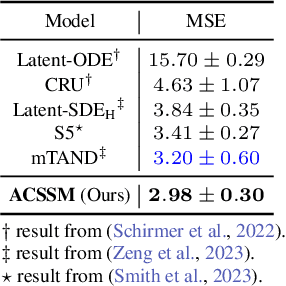
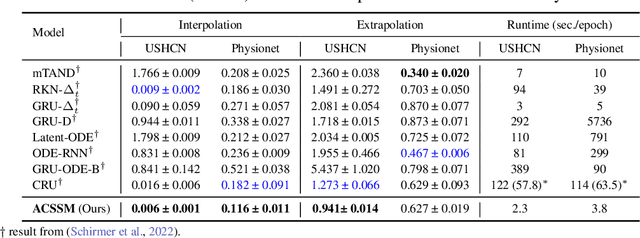
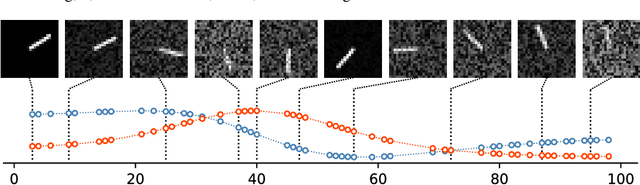
Many real-world datasets, such as healthcare, climate, and economics, are often collected as irregular time series, which poses challenges for accurate modeling. In this paper, we propose the Amortized Control of continuous State Space Model (ACSSM) for continuous dynamical modeling of time series for irregular and discrete observations. We first present a multi-marginal Doob's $h$-transform to construct a continuous dynamical system conditioned on these irregular observations. Following this, we introduce a variational inference algorithm with a tight evidence lower bound (ELBO), leveraging stochastic optimal control (SOC) theory to approximate the intractable Doob's $h$-transform and simulate the conditioned dynamics. To improve efficiency and scalability during both training and inference, ACSSM employs amortized inference to decouple representation learning from the latent dynamics. Additionally, it incorporates a simulation-free latent dynamics framework and a transformer-based data assimilation scheme, facilitating parallel inference of the latent states and ELBO computation. Through empirical evaluations across a variety of real-world datasets, ACSSM demonstrates superior performance in tasks such as classification, regression, interpolation, and extrapolation, while maintaining computational efficiency.

Enhancing Transfer Learning with Flexible Nonparametric Posterior Sampling

Transfer learning has recently shown significant performance across various tasks involving deep neural networks. In these transfer learning scenarios, the prior distribution for downstream data becomes crucial in Bayesian model averaging (BMA). While previous works proposed the prior over the neural network parameters centered around the pre-trained solution, such strategies have limitations when dealing with distribution shifts between upstream and downstream data. This paper introduces nonparametric transfer learning (NPTL), a flexible posterior sampling method to address the distribution shift issue within the context of nonparametric learning. The nonparametric learning (NPL) method is a recent approach that employs a nonparametric prior for posterior sampling, efficiently accounting for model misspecification scenarios, which is suitable for transfer learning scenarios that may involve the distribution shift between upstream and downstream tasks. Through extensive empirical validations, we demonstrate that our approach surpasses other baselines in BMA performance.

Joint-Embedding Masked Autoencoder for Self-supervised Learning of Dynamic Functional Connectivity from the Human Brain

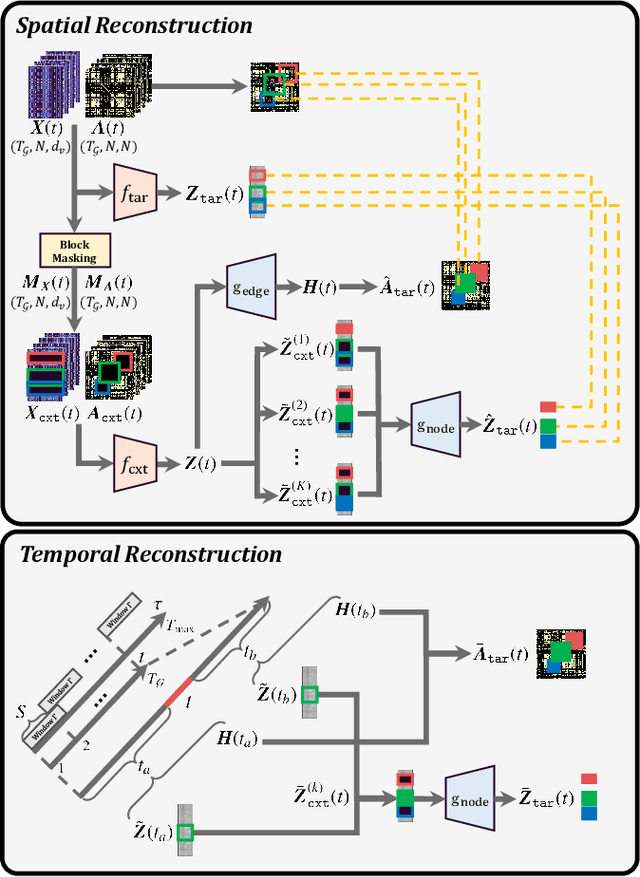
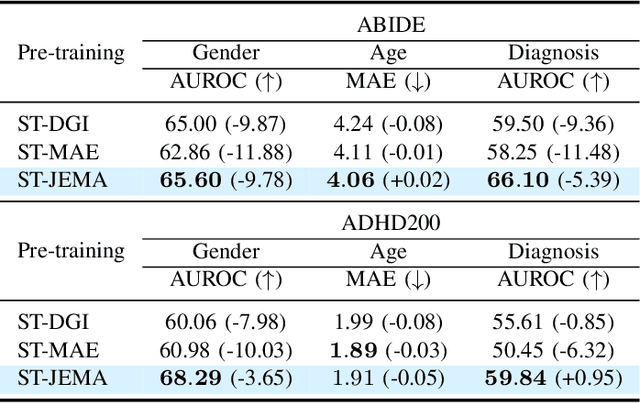
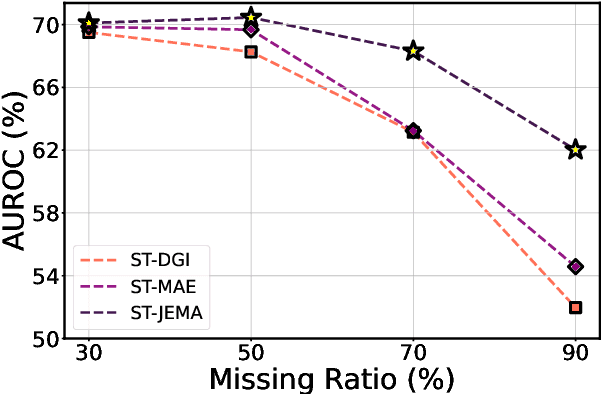
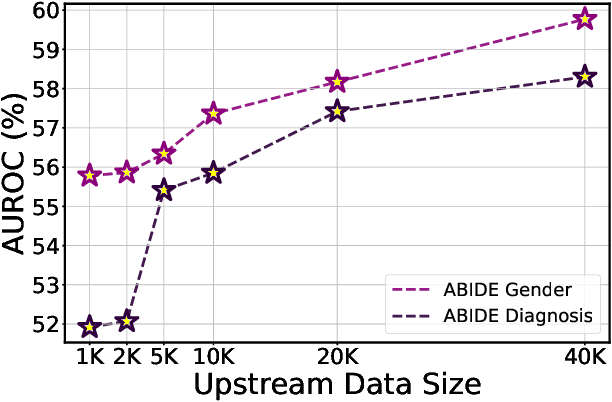
Graph Neural Networks (GNNs) have shown promise in learning dynamic functional connectivity for distinguishing phenotypes from human brain networks. However, obtaining extensive labeled clinical data for training is often resource-intensive, making practical application difficult. Leveraging unlabeled data thus becomes crucial for representation learning in a label-scarce setting. Although generative self-supervised learning techniques, especially masked autoencoders, have shown promising results in representation learning in various domains, their application to dynamic graphs for dynamic functional connectivity remains underexplored, facing challenges in capturing high-level semantic representations. Here, we introduce the Spatio-Temporal Joint Embedding Masked Autoencoder (ST-JEMA), drawing inspiration from the Joint Embedding Predictive Architecture (JEPA) in computer vision. ST-JEMA employs a JEPA-inspired strategy for reconstructing dynamic graphs, which enables the learning of higher-level semantic representations considering temporal perspectives, addressing the challenges in fMRI data representation learning. Utilizing the large-scale UK Biobank dataset for self-supervised learning, ST-JEMA shows exceptional representation learning performance on dynamic functional connectivity demonstrating superiority over previous methods in predicting phenotypes and psychiatric diagnoses across eight benchmark fMRI datasets even with limited samples and effectiveness of temporal reconstruction on missing data scenarios. These findings highlight the potential of our approach as a robust representation learning method for leveraging label-scarce fMRI data.

Function Space Bayesian Pseudocoreset for Bayesian Neural Networks

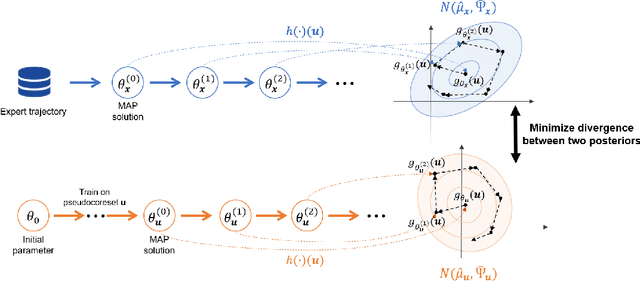
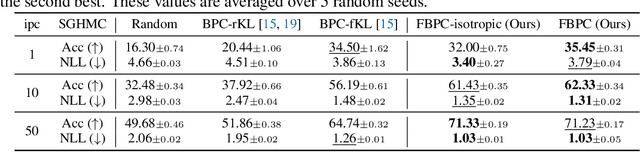
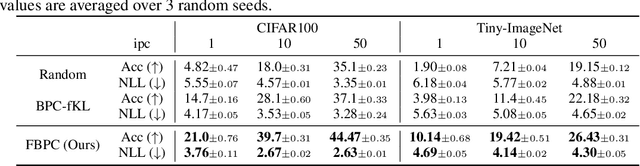
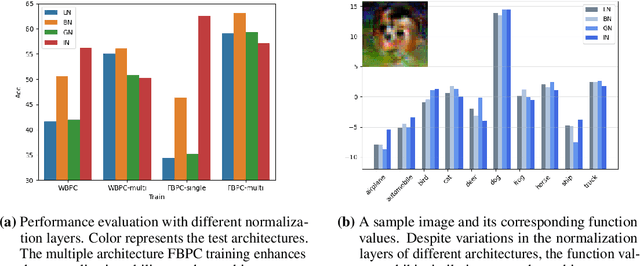
A Bayesian pseudocoreset is a compact synthetic dataset summarizing essential information of a large-scale dataset and thus can be used as a proxy dataset for scalable Bayesian inference. Typically, a Bayesian pseudocoreset is constructed by minimizing a divergence measure between the posterior conditioning on the pseudocoreset and the posterior conditioning on the full dataset. However, evaluating the divergence can be challenging, particularly for the models like deep neural networks having high-dimensional parameters. In this paper, we propose a novel Bayesian pseudocoreset construction method that operates on a function space. Unlike previous methods, which construct and match the coreset and full data posteriors in the space of model parameters (weights), our method constructs variational approximations to the coreset posterior on a function space and matches it to the full data posterior in the function space. By working directly on the function space, our method could bypass several challenges that may arise when working on a weight space, including limited scalability and multi-modality issue. Through various experiments, we demonstrate that the Bayesian pseudocoresets constructed from our method enjoys enhanced uncertainty quantification and better robustness across various model architectures.

Traversing Between Modes in Function Space for Fast Ensembling

Deep ensemble is a simple yet powerful way to improve the performance of deep neural networks. Under this motivation, recent works on mode connectivity have shown that parameters of ensembles are connected by low-loss subspaces, and one can efficiently collect ensemble parameters in those subspaces. While this provides a way to efficiently train ensembles, for inference, multiple forward passes should still be executed using all the ensemble parameters, which often becomes a serious bottleneck for real-world deployment. In this work, we propose a novel framework to reduce such costs. Given a low-loss subspace connecting two modes of a neural network, we build an additional neural network that predicts the output of the original neural network evaluated at a certain point in the low-loss subspace. The additional neural network, which we call a "bridge", is a lightweight network that takes minimal features from the original network and predicts outputs for the low-loss subspace without forward passes through the original network. We empirically demonstrate that we can indeed train such bridge networks and significantly reduce inference costs with the help of bridge networks.

Regularizing Towards Soft Equivariance Under Mixed Symmetries

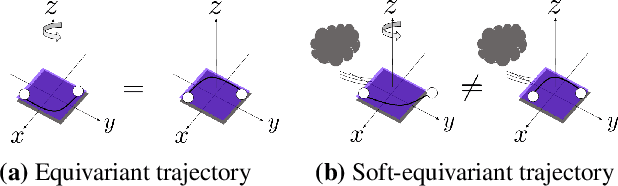
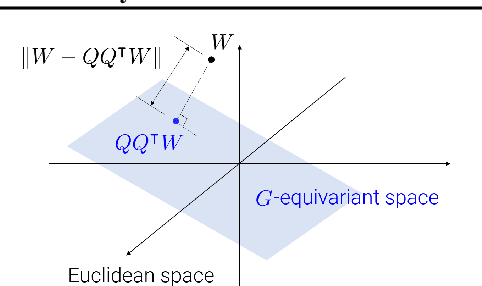
Datasets often have their intrinsic symmetries, and particular deep-learning models called equivariant or invariant models have been developed to exploit these symmetries. However, if some or all of these symmetries are only approximate, which frequently happens in practice, these models may be suboptimal due to the architectural restrictions imposed on them. We tackle this issue of approximate symmetries in a setup where symmetries are mixed, i.e., they are symmetries of not single but multiple different types and the degree of approximation varies across these types. Instead of proposing a new architectural restriction as in most of the previous approaches, we present a regularizer-based method for building a model for a dataset with mixed approximate symmetries. The key component of our method is what we call equivariance regularizer for a given type of symmetries, which measures how much a model is equivariant with respect to the symmetries of the type. Our method is trained with these regularizers, one per each symmetry type, and the strength of the regularizers is automatically tuned during training, leading to the discovery of the approximation levels of some candidate symmetry types without explicit supervision. Using synthetic function approximation and motion forecasting tasks, we demonstrate that our method achieves better accuracy than prior approaches while discovering the approximate symmetry levels correctly.

SWAMP: Sparse Weight Averaging with Multiple Particles for Iterative Magnitude Pruning

Given the ever-increasing size of modern neural networks, the significance of sparse architectures has surged due to their accelerated inference speeds and minimal memory demands. When it comes to global pruning techniques, Iterative Magnitude Pruning (IMP) still stands as a state-of-the-art algorithm despite its simple nature, particularly in extremely sparse regimes. In light of the recent finding that the two successive matching IMP solutions are linearly connected without a loss barrier, we propose Sparse Weight Averaging with Multiple Particles (SWAMP), a straightforward modification of IMP that achieves performance comparable to an ensemble of two IMP solutions. For every iteration, we concurrently train multiple sparse models, referred to as particles, using different batch orders yet the same matching ticket, and then weight average such models to produce a single mask. We demonstrate that our method consistently outperforms existing baselines across different sparsities through extensive experiments on various data and neural network structures.