A Foundational Brain Dynamics Model via Stochastic Optimal Control

We introduce a foundational model for brain dynamics that utilizes stochastic optimal control (SOC) and amortized inference. Our method features a continuous-discrete state space model (SSM) that can robustly handle the intricate and noisy nature of fMRI signals. To address computational limitations, we implement an approximation strategy grounded in the SOC framework. Additionally, we present a simulation-free latent dynamics approach that employs locally linear approximations, facilitating efficient and scalable inference. For effective representation learning, we derive an Evidence Lower Bound (ELBO) from the SOC formulation, which integrates smoothly with recent advancements in self-supervised learning (SSL), thereby promoting robust and transferable representations. Pre-trained on extensive datasets such as the UKB, our model attains state-of-the-art results across a variety of downstream tasks, including demographic prediction, trait analysis, disease diagnosis, and prognosis. Moreover, evaluating on external datasets such as HCP-A, ABIDE, and ADHD200 further validates its superior abilities and resilience across different demographic and clinical distributions. Our foundational model provides a scalable and efficient approach for deciphering brain dynamics, opening up numerous applications in neuroscience.

Amortized Control of Continuous State Space Feynman-Kac Model for Irregular Time Series

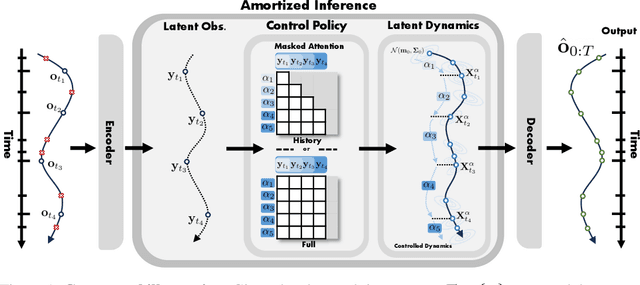
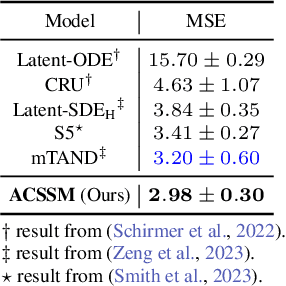
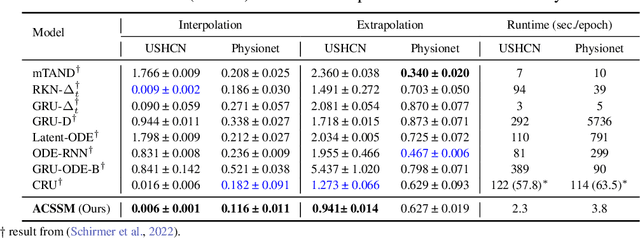
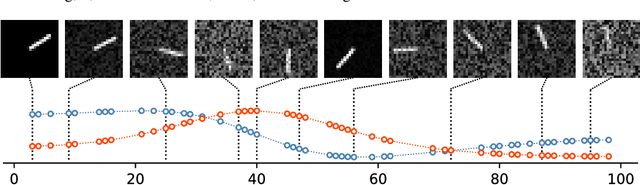
Many real-world datasets, such as healthcare, climate, and economics, are often collected as irregular time series, which poses challenges for accurate modeling. In this paper, we propose the Amortized Control of continuous State Space Model (ACSSM) for continuous dynamical modeling of time series for irregular and discrete observations. We first present a multi-marginal Doob's $h$-transform to construct a continuous dynamical system conditioned on these irregular observations. Following this, we introduce a variational inference algorithm with a tight evidence lower bound (ELBO), leveraging stochastic optimal control (SOC) theory to approximate the intractable Doob's $h$-transform and simulate the conditioned dynamics. To improve efficiency and scalability during both training and inference, ACSSM employs amortized inference to decouple representation learning from the latent dynamics. Additionally, it incorporates a simulation-free latent dynamics framework and a transformer-based data assimilation scheme, facilitating parallel inference of the latent states and ELBO computation. Through empirical evaluations across a variety of real-world datasets, ACSSM demonstrates superior performance in tasks such as classification, regression, interpolation, and extrapolation, while maintaining computational efficiency.

Stochastic Optimal Control for Diffusion Bridges in Function Spaces

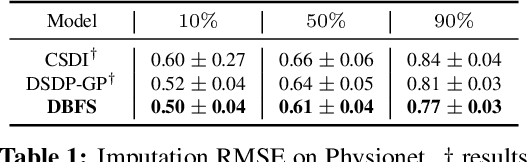
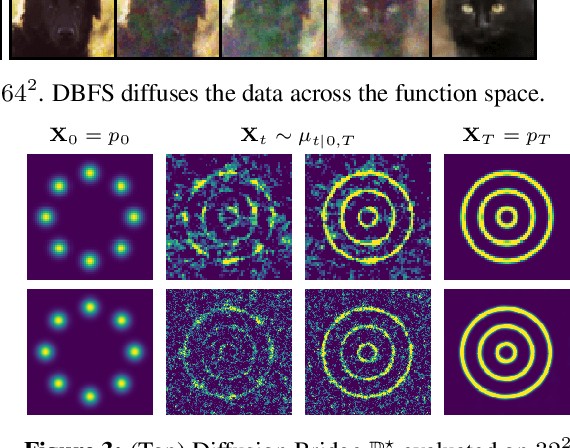
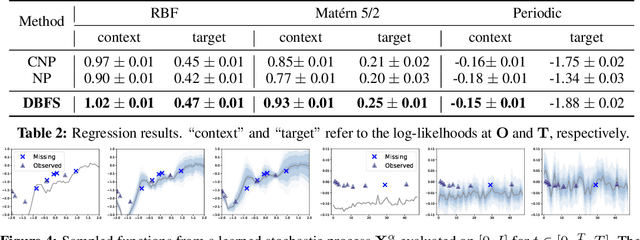
Recent advancements in diffusion models and diffusion bridges primarily focus on finite-dimensional spaces, yet many real-world problems necessitate operations in infinite-dimensional function spaces for more natural and interpretable formulations. In this paper, we present a theory of stochastic optimal control (SOC) tailored to infinite-dimensional spaces, aiming to extend diffusion-based algorithms to function spaces. Specifically, we demonstrate how Doob's $h$-transform, the fundamental tool for constructing diffusion bridges, can be derived from the SOC perspective and expanded to infinite dimensions. This expansion presents a challenge, as infinite-dimensional spaces typically lack closed-form densities. Leveraging our theory, we establish that solving the optimal control problem with a specific objective function choice is equivalent to learning diffusion-based generative models. We propose two applications: (1) learning bridges between two infinite-dimensional distributions and (2) generative models for sampling from an infinite-dimensional distribution. Our approach proves effective for diverse problems involving continuous function space representations, such as resolution-free images, time-series data, and probability density functions.