Stochastic Optimal Control for Diffusion Bridges in Function Spaces
Paper and Code
Jun 03, 2024
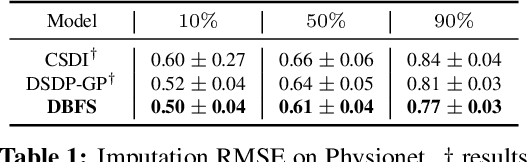
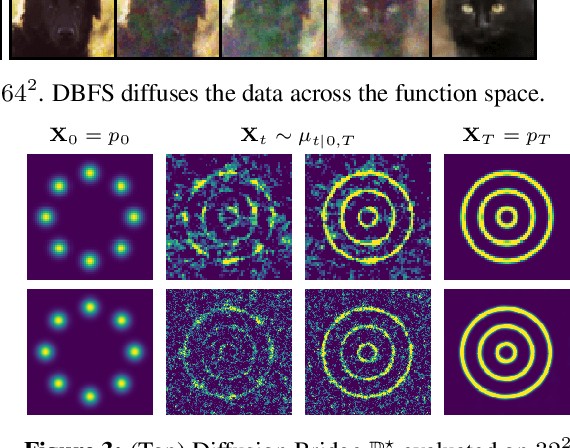
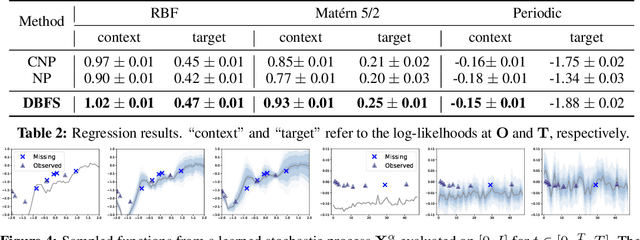
Recent advancements in diffusion models and diffusion bridges primarily focus on finite-dimensional spaces, yet many real-world problems necessitate operations in infinite-dimensional function spaces for more natural and interpretable formulations. In this paper, we present a theory of stochastic optimal control (SOC) tailored to infinite-dimensional spaces, aiming to extend diffusion-based algorithms to function spaces. Specifically, we demonstrate how Doob's $h$-transform, the fundamental tool for constructing diffusion bridges, can be derived from the SOC perspective and expanded to infinite dimensions. This expansion presents a challenge, as infinite-dimensional spaces typically lack closed-form densities. Leveraging our theory, we establish that solving the optimal control problem with a specific objective function choice is equivalent to learning diffusion-based generative models. We propose two applications: (1) learning bridges between two infinite-dimensional distributions and (2) generative models for sampling from an infinite-dimensional distribution. Our approach proves effective for diverse problems involving continuous function space representations, such as resolution-free images, time-series data, and probability density functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge