Bounding Consideration Probabilities in Consider-Then-Choose Ranking Models

A common theory of choice posits that individuals make choices in a two-step process, first selecting some subset of the alternatives to consider before making a selection from the resulting consideration set. However, inferring unobserved consideration sets (or item consideration probabilities) in this "consider then choose" setting poses significant challenges, because even simple models of consideration with strong independence assumptions are not identifiable, even if item utilities are known. We consider a natural extension of consider-then-choose models to a top-$k$ ranking setting, where we assume rankings are constructed according to a Plackett-Luce model after sampling a consideration set. While item consideration probabilities remain non-identified in this setting, we prove that knowledge of item utilities allows us to infer bounds on the relative sizes of consideration probabilities. Additionally, given a condition on the expected consideration set size, we derive absolute upper and lower bounds on item consideration probabilities. We also provide algorithms to tighten those bounds on consideration probabilities by propagating inferred constraints. Thus, we show that we can learn useful information about consideration probabilities despite not being able to identify them precisely. We demonstrate our methods on a ranking dataset from a psychology experiment with two different ranking tasks (one with fixed consideration sets and one with unknown consideration sets). This combination of data allows us to estimate utilities and then learn about unknown consideration probabilities using our bounds.

Graph-Based Methods for Discrete Choice

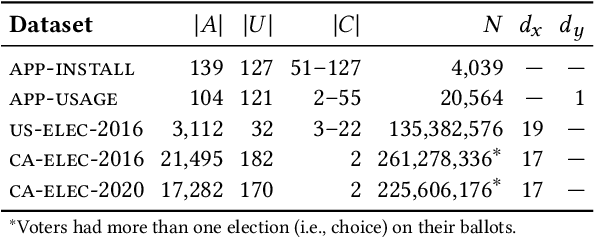
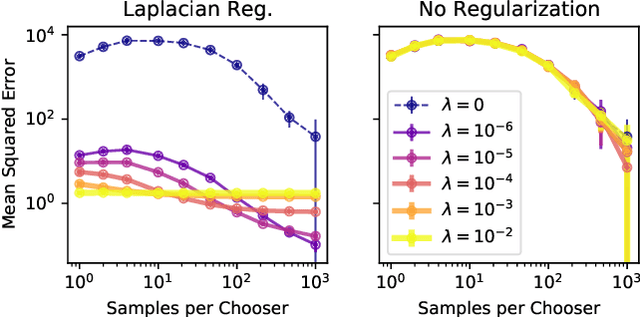
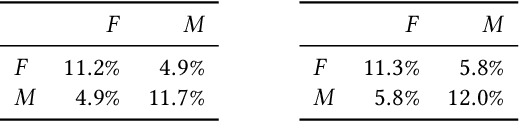
Choices made by individuals have widespread impacts--for instance, people choose between political candidates to vote for, between social media posts to share, and between brands to purchase--moreover, data on these choices are increasingly abundant. Discrete choice models are a key tool for learning individual preferences from such data. Additionally, social factors like conformity and contagion influence individual choice. Existing methods for incorporating these factors into choice models do not account for the entire social network and require hand-crafted features. To overcome these limitations, we use graph learning to study choice in networked contexts. We identify three ways in which graph learning techniques can be used for discrete choice: learning chooser representations, regularizing choice model parameters, and directly constructing predictions from a network. We design methods in each category and test them on real-world choice datasets, including county-level 2016 US election results and Android app installation and usage data. We show that incorporating social network structure can improve the predictions of the standard econometric choice model, the multinomial logit. We provide evidence that app installations are influenced by social context, but we find no such effect on app usage among the same participants, which instead is habit-driven. In the election data, we highlight the additional insights a discrete choice framework provides over classification or regression, the typical approaches. On synthetic data, we demonstrate the sample complexity benefit of using social information in choice models.

Choice Set Confounding in Discrete Choice

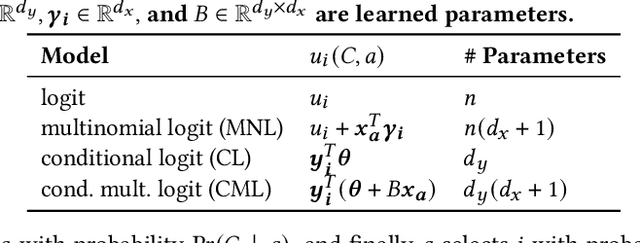
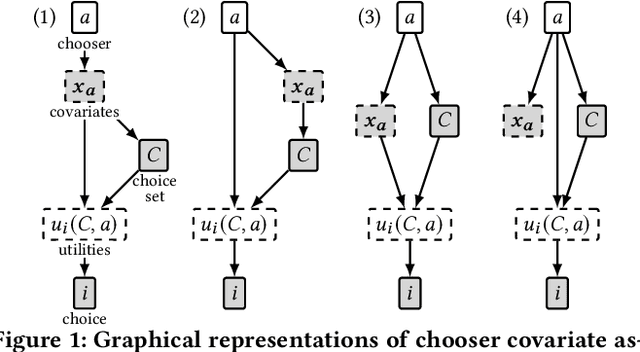
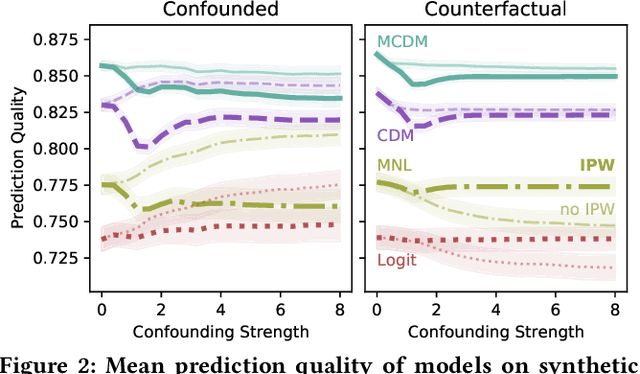
Standard methods in preference learning involve estimating the parameters of discrete choice models from data of selections (choices) made by individuals from a discrete set of alternatives (the choice set). While there are many models for individual preferences, existing learning methods overlook how choice set assignment affects the data. Often, the choice set itself is influenced by an individual's preferences; for instance, a consumer choosing a product from an online retailer is often presented with options from a recommender system that depend on information about the consumer's preferences. Ignoring these assignment mechanisms can mislead choice models into making biased estimates of preferences, a phenomenon that we call choice set confounding; we demonstrate the presence of such confounding in widely-used choice datasets. To address this issue, we adapt methods from causal inference to the discrete choice setting. We use covariates of the chooser for inverse probability weighting and/or regression controls, accurately recovering individual preferences in the presence of choice set confounding under certain assumptions. When such covariates are unavailable or inadequate, we develop methods that take advantage of structured choice set assignment to improve prediction. We demonstrate the effectiveness of our methods on real-world choice data, showing, for example, that accounting for choice set confounding makes choices observed in hotel booking and commute transportation more consistent with rational utility-maximization.

Learning Interpretable Feature Context Effects in Discrete Choice

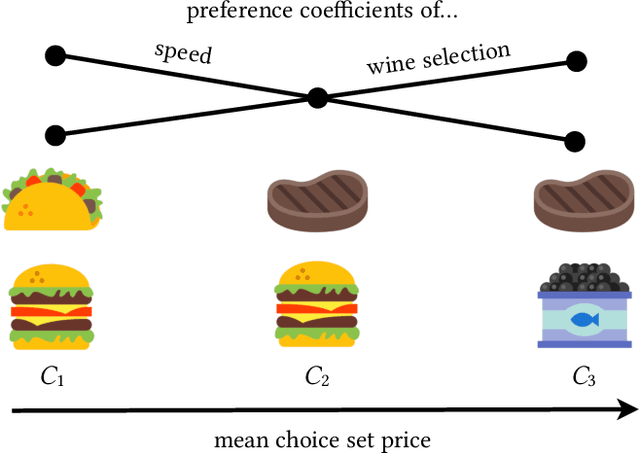
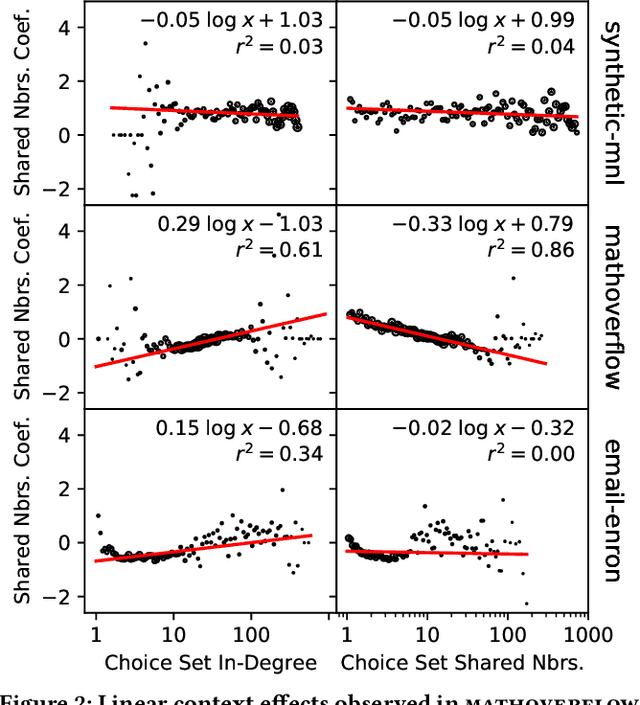
The outcomes of elections, product sales, and the structure of social connections are all determined by the choices individuals make when presented with a set of options, so understanding the factors that contribute to choice is crucial. Of particular interest are context effects, which occur when the set of available options influences a chooser's relative preferences, as they violate traditional rationality assumptions yet are widespread in practice. However, identifying these effects from observed choices is challenging, often requiring foreknowledge of the effect to be measured. In contrast, we provide a method for the automatic discovery of a broad class of context effects from observed choice data. Our models are easier to train and more flexible than existing models and also yield intuitive, interpretable, and statistically testable context effects. Using our models, we identify new context effects in widely used choice datasets and provide the first analysis of choice set context effects in social network growth.

Choice Set Optimization Under Discrete Choice Models of Group Decisions

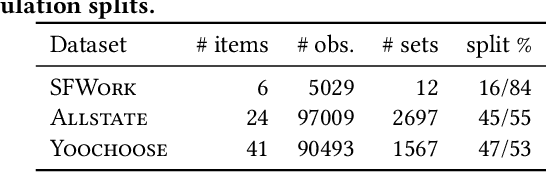
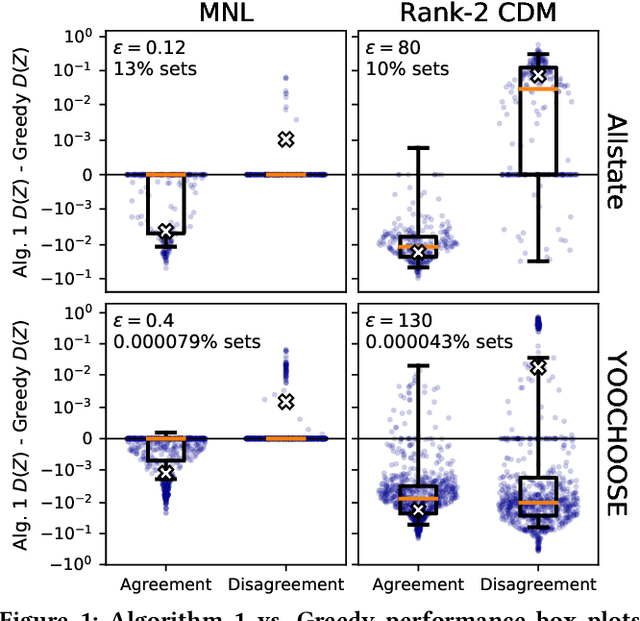
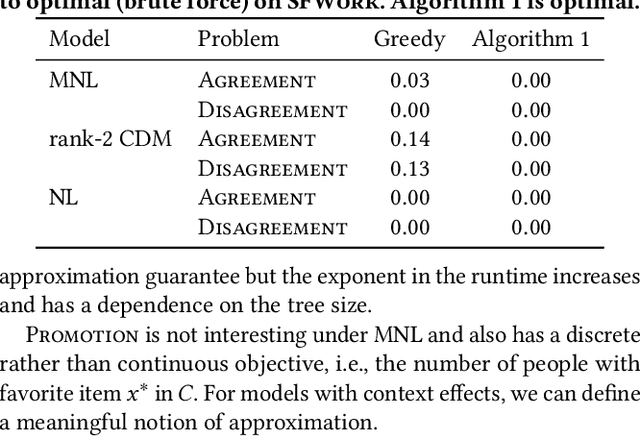
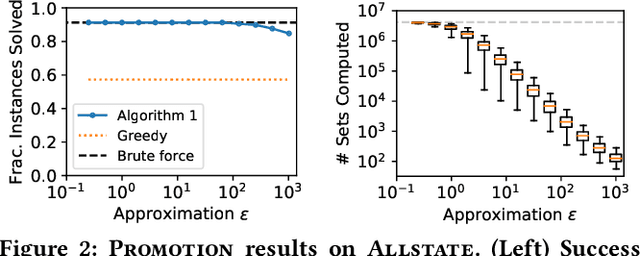
The way that people make choices or exhibit preferences can be strongly affected by the set of available alternatives, often called the choice set. Furthermore, there are usually heterogeneous preferences, either at an individual level within small groups or within sub-populations of large groups. Given the availability of choice data, there are now many models that capture this behavior in order to make effective predictions. However, there is little work in understanding how directly changing the choice set can be used to influence a group's preferences or decisions. Here, we use discrete choice modeling to develop an optimization framework of such interventions for several problems of group influence, including maximizing agreement or disagreement and promoting a particular choice. We show that these problems are NP-hard in general but imposing restrictions reveals a fundamental boundary: promoting an item is easier than maximizing agreement or disagreement. After, we design approximation algorithms for the hard problems and show that they work extremely well for real-world choice data.