Understanding Non-linearity in Graph Neural Networks from the Bayesian-Inference Perspective

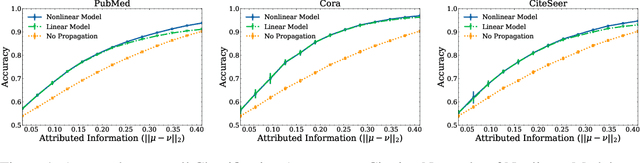
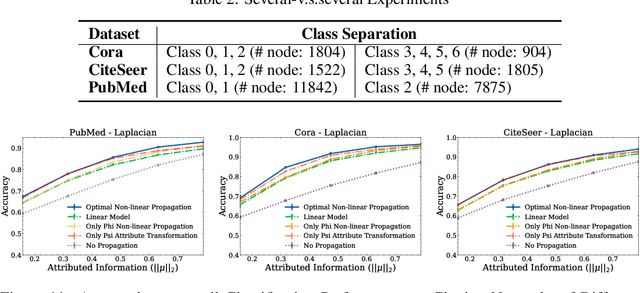
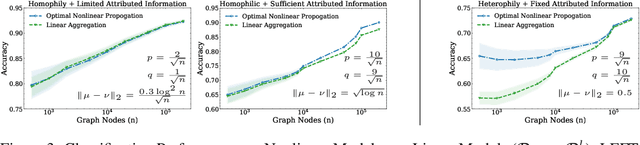
Graph neural networks (GNNs) have shown superiority in many prediction tasks over graphs due to their impressive capability of capturing nonlinear relations in graph-structured data. However, for node classification tasks, often, only marginal improvement of GNNs over their linear counterparts has been observed. Previous works provide very few understandings of this phenomenon. In this work, we resort to Bayesian learning to deeply investigate the functions of non-linearity in GNNs for node classification tasks. Given a graph generated from the statistical model CSBM, we observe that the max-a-posterior estimation of a node label given its own and neighbors' attributes consists of two types of non-linearity, a possibly non-linear transformation of node attributes and a ReLU-activated feature aggregation from neighbors. The latter surprisingly matches the type of non-linearity used in many GNN models. By further imposing Gaussian assumption on node attributes, we prove that the superiority of those ReLU activations is only significant when the node attributes are far more informative than the graph structure, which nicely matches many previous empirical observations. A similar argument can be achieved when there is a distribution shift of node attributes between the training and testing datasets. Finally, we verify our theory on both synthetic and real-world networks.