Rongzhe Wei
GRIP: Algorithm-Agnostic Machine Unlearning for Mixture-of-Experts via Geometric Router Constraints
Jan 23, 2026Abstract:Machine unlearning (MU) for large language models has become critical for AI safety, yet existing methods fail to generalize to Mixture-of-Experts (MoE) architectures. We identify that traditional unlearning methods exploit MoE's architectural vulnerability: they manipulate routers to redirect queries away from knowledgeable experts rather than erasing knowledge, causing a loss of model utility and superficial forgetting. We propose Geometric Routing Invariance Preservation (GRIP), an algorithm-agnostic framework for unlearning for MoE. Our core contribution is a geometric constraint, implemented by projecting router gradient updates into an expert-specific null-space. Crucially, this decouples routing stability from parameter rigidity: while discrete expert selections remain stable for retained knowledge, the continuous router parameters remain plastic within the null space, allowing the model to undergo necessary internal reconfiguration to satisfy unlearning objectives. This forces the unlearning optimization to erase knowledge directly from expert parameters rather than exploiting the superficial router manipulation shortcut. GRIP functions as an adapter, constraining router parameter updates without modifying the underlying unlearning algorithm. Extensive experiments on large-scale MoE models demonstrate that our adapter eliminates expert selection shift (achieving over 95% routing stability) across all tested unlearning methods while preserving their utility. By preventing existing algorithms from exploiting MoE model's router vulnerability, GRIP adapts existing unlearning research from dense architectures to MoEs.
Differentially Private Relational Learning with Entity-level Privacy Guarantees
Jun 10, 2025Abstract:Learning with relational and network-structured data is increasingly vital in sensitive domains where protecting the privacy of individual entities is paramount. Differential Privacy (DP) offers a principled approach for quantifying privacy risks, with DP-SGD emerging as a standard mechanism for private model training. However, directly applying DP-SGD to relational learning is challenging due to two key factors: (i) entities often participate in multiple relations, resulting in high and difficult-to-control sensitivity; and (ii) relational learning typically involves multi-stage, potentially coupled (interdependent) sampling procedures that make standard privacy amplification analyses inapplicable. This work presents a principled framework for relational learning with formal entity-level DP guarantees. We provide a rigorous sensitivity analysis and introduce an adaptive gradient clipping scheme that modulates clipping thresholds based on entity occurrence frequency. We also extend the privacy amplification results to a tractable subclass of coupled sampling, where the dependence arises only through sample sizes. These contributions lead to a tailored DP-SGD variant for relational data with provable privacy guarantees. Experiments on fine-tuning text encoders over text-attributed network-structured relational data demonstrate the strong utility-privacy trade-offs of our approach. Our code is available at https://github.com/Graph-COM/Node_DP.
Do LLMs Really Forget? Evaluating Unlearning with Knowledge Correlation and Confidence Awareness
Jun 06, 2025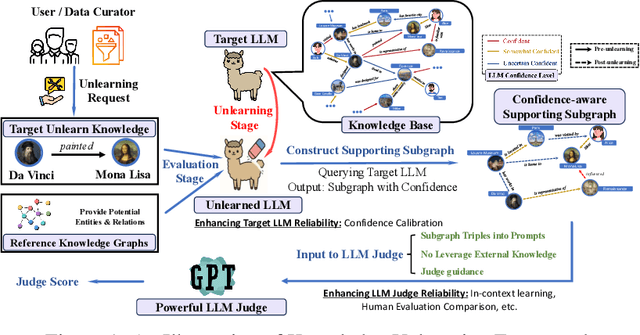
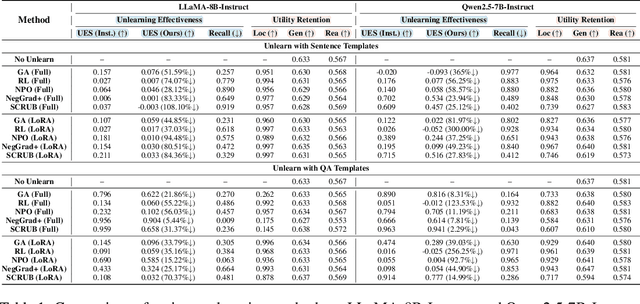
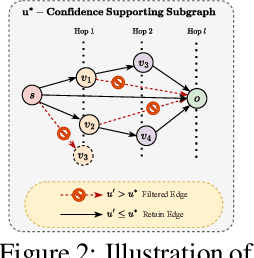
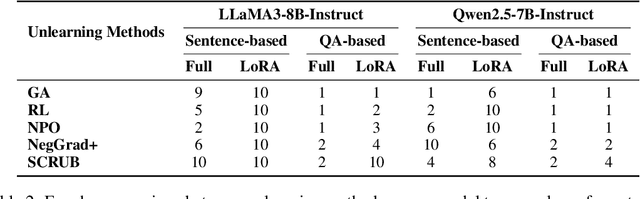
Abstract:Machine unlearning techniques aim to mitigate unintended memorization in large language models (LLMs). However, existing approaches predominantly focus on the explicit removal of isolated facts, often overlooking latent inferential dependencies and the non-deterministic nature of knowledge within LLMs. Consequently, facts presumed forgotten may persist implicitly through correlated information. To address these challenges, we propose a knowledge unlearning evaluation framework that more accurately captures the implicit structure of real-world knowledge by representing relevant factual contexts as knowledge graphs with associated confidence scores. We further develop an inference-based evaluation protocol leveraging powerful LLMs as judges; these judges reason over the extracted knowledge subgraph to determine unlearning success. Our LLM judges utilize carefully designed prompts and are calibrated against human evaluations to ensure their trustworthiness and stability. Extensive experiments on our newly constructed benchmark demonstrate that our framework provides a more realistic and rigorous assessment of unlearning performance. Moreover, our findings reveal that current evaluation strategies tend to overestimate unlearning effectiveness. Our code is publicly available at https://github.com/Graph-COM/Knowledge_Unlearning.git.
Model Generalization on Text Attribute Graphs: Principles with Large Language Models
Feb 17, 2025Abstract:Large language models (LLMs) have recently been introduced to graph learning, aiming to extend their zero-shot generalization success to tasks where labeled graph data is scarce. Among these applications, inference over text-attributed graphs (TAGs) presents unique challenges: existing methods struggle with LLMs' limited context length for processing large node neighborhoods and the misalignment between node embeddings and the LLM token space. To address these issues, we establish two key principles for ensuring generalization and derive the framework LLM-BP accordingly: (1) Unifying the attribute space with task-adaptive embeddings, where we leverage LLM-based encoders and task-aware prompting to enhance generalization of the text attribute embeddings; (2) Developing a generalizable graph information aggregation mechanism, for which we adopt belief propagation with LLM-estimated parameters that adapt across graphs. Evaluations on 11 real-world TAG benchmarks demonstrate that LLM-BP significantly outperforms existing approaches, achieving 8.10% improvement with task-conditional embeddings and an additional 1.71% gain from adaptive aggregation.
Underestimated Privacy Risks for Minority Populations in Large Language Model Unlearning
Dec 11, 2024Abstract:Large Language Models are trained on extensive datasets that often contain sensitive, human-generated information, raising significant concerns about privacy breaches. While certified unlearning approaches offer strong privacy guarantees, they rely on restrictive model assumptions that are not applicable to LLMs. As a result, various unlearning heuristics have been proposed, with the associated privacy risks assessed only empirically. The standard evaluation pipelines typically randomly select data for removal from the training set, apply unlearning techniques, and use membership inference attacks to compare the unlearned models against models retrained without the to-be-unlearned data. However, since every data point is subject to the right to be forgotten, unlearning should be considered in the worst-case scenario from the privacy perspective. Prior work shows that data outliers may exhibit higher memorization effects. Intuitively, they are harder to be unlearn and thus the privacy risk of unlearning them is underestimated in the current evaluation. In this paper, we leverage minority data to identify such a critical flaw in previously widely adopted evaluations. We substantiate this claim through carefully designed experiments, including unlearning canaries related to minority groups, inspired by privacy auditing literature. Using personally identifiable information as a representative minority identifier, we demonstrate that minority groups experience at least 20% more privacy leakage in most cases across six unlearning approaches, three MIAs, three benchmark datasets, and two LLMs of different scales. Given that the right to be forgotten should be upheld for every individual, we advocate for a more rigorous evaluation of LLM unlearning methods. Our minority-aware evaluation framework represents an initial step toward ensuring more equitable assessments of LLM unlearning efficacy.
Privately Learning from Graphs with Applications in Fine-tuning Large Language Models
Oct 10, 2024



Abstract:Graphs offer unique insights into relationships and interactions between entities, complementing data modalities like text, images, and videos. By incorporating relational information from graph data, AI models can extend their capabilities beyond traditional tasks. However, relational data in sensitive domains such as finance and healthcare often contain private information, making privacy preservation crucial. Existing privacy-preserving methods, such as DP-SGD, which rely on gradient decoupling assumptions, are not well-suited for relational learning due to the inherent dependencies between coupled training samples. To address this challenge, we propose a privacy-preserving relational learning pipeline that decouples dependencies in sampled relations during training, ensuring differential privacy through a tailored application of DP-SGD. We apply this method to fine-tune large language models (LLMs) on sensitive graph data, and tackle the associated computational complexities. Our approach is evaluated on LLMs of varying sizes (e.g., BERT, Llama2) using real-world relational data from four text-attributed graphs. The results demonstrate significant improvements in relational learning tasks, all while maintaining robust privacy guarantees during training. Additionally, we explore the trade-offs between privacy, utility, and computational efficiency, offering insights into the practical deployment of our approach. Code is available at https://github.com/Graph-COM/PvGaLM.
Differentially Private Graph Diffusion with Applications in Personalized PageRanks
Jul 02, 2024



Abstract:Graph diffusion, which iteratively propagates real-valued substances among the graph, is used in numerous graph/network-involved applications. However, releasing diffusion vectors may reveal sensitive linking information in the data such as transaction information in financial network data. However, protecting the privacy of graph data is challenging due to its interconnected nature. This work proposes a novel graph diffusion framework with edge-level differential privacy guarantees by using noisy diffusion iterates. The algorithm injects Laplace noise per diffusion iteration and adopts a degree-based thresholding function to mitigate the high sensitivity induced by low-degree nodes. Our privacy loss analysis is based on Privacy Amplification by Iteration (PABI), which to our best knowledge, is the first effort that analyzes PABI with Laplace noise and provides relevant applications. We also introduce a novel Infinity-Wasserstein distance tracking method, which tightens the analysis of privacy leakage and makes PABI more applicable in practice. We evaluate this framework by applying it to Personalized Pagerank computation for ranking tasks. Experiments on real-world network data demonstrate the superiority of our method under stringent privacy conditions.
Learning Scalable Structural Representations for Link Prediction with Bloom Signatures
Dec 28, 2023



Abstract:Graph neural networks (GNNs) have shown great potential in learning on graphs, but they are known to perform sub-optimally on link prediction tasks. Existing GNNs are primarily designed to learn node-wise representations and usually fail to capture pairwise relations between target nodes, which proves to be crucial for link prediction. Recent works resort to learning more expressive edge-wise representations by enhancing vanilla GNNs with structural features such as labeling tricks and link prediction heuristics, but they suffer from high computational overhead and limited scalability. To tackle this issue, we propose to learn structural link representations by augmenting the message-passing framework of GNNs with Bloom signatures. Bloom signatures are hashing-based compact encodings of node neighborhoods, which can be efficiently merged to recover various types of edge-wise structural features. We further show that any type of neighborhood overlap-based heuristic can be estimated by a neural network that takes Bloom signatures as input. GNNs with Bloom signatures are provably more expressive than vanilla GNNs and also more scalable than existing edge-wise models. Experimental results on five standard link prediction benchmarks show that our proposed model achieves comparable or better performance than existing edge-wise GNN models while being 3-200 $\times$ faster and more memory-efficient for online inference.
On the Inherent Privacy Properties of Discrete Denoising Diffusion Models
Oct 24, 2023



Abstract:Privacy concerns have led to a surge in the creation of synthetic datasets, with diffusion models emerging as a promising avenue. Although prior studies have performed empirical evaluations on these models, there has been a gap in providing a mathematical characterization of their privacy-preserving capabilities. To address this, we present the pioneering theoretical exploration of the privacy preservation inherent in discrete diffusion models (DDMs) for discrete dataset generation. Focusing on per-instance differential privacy (pDP), our framework elucidates the potential privacy leakage for each data point in a given training dataset, offering insights into data preprocessing to reduce privacy risks of the synthetic dataset generation via DDMs. Our bounds also show that training with $s$-sized data points leads to a surge in privacy leakage from $(\epsilon, \mathcal{O}(\frac{1}{s^2\epsilon}))$-pDP to $(\epsilon, \mathcal{O}(\frac{1}{s\epsilon}))$-pDP during the transition from the pure noise to the synthetic clean data phase, and a faster decay in diffusion coefficients amplifies the privacy guarantee. Finally, we empirically verify our theoretical findings on both synthetic and real-world datasets.
Understanding Non-linearity in Graph Neural Networks from the Bayesian-Inference Perspective
Jul 27, 2022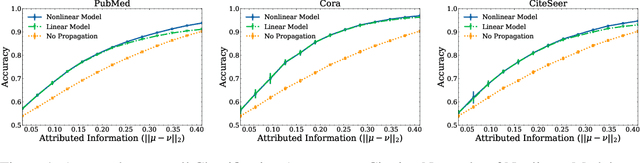

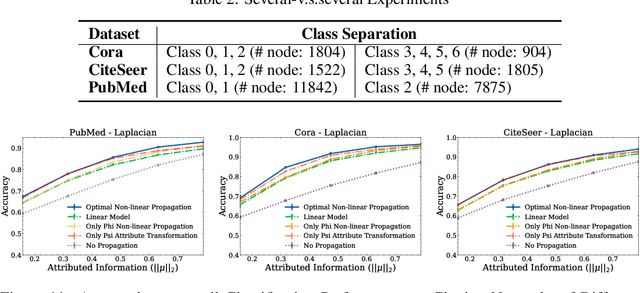
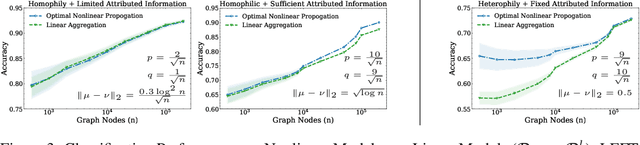
Abstract:Graph neural networks (GNNs) have shown superiority in many prediction tasks over graphs due to their impressive capability of capturing nonlinear relations in graph-structured data. However, for node classification tasks, often, only marginal improvement of GNNs over their linear counterparts has been observed. Previous works provide very few understandings of this phenomenon. In this work, we resort to Bayesian learning to deeply investigate the functions of non-linearity in GNNs for node classification tasks. Given a graph generated from the statistical model CSBM, we observe that the max-a-posterior estimation of a node label given its own and neighbors' attributes consists of two types of non-linearity, a possibly non-linear transformation of node attributes and a ReLU-activated feature aggregation from neighbors. The latter surprisingly matches the type of non-linearity used in many GNN models. By further imposing Gaussian assumption on node attributes, we prove that the superiority of those ReLU activations is only significant when the node attributes are far more informative than the graph structure, which nicely matches many previous empirical observations. A similar argument can be achieved when there is a distribution shift of node attributes between the training and testing datasets. Finally, we verify our theory on both synthetic and real-world networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge