Graph Belief Propagation Networks
Paper and Code
Jun 06, 2021
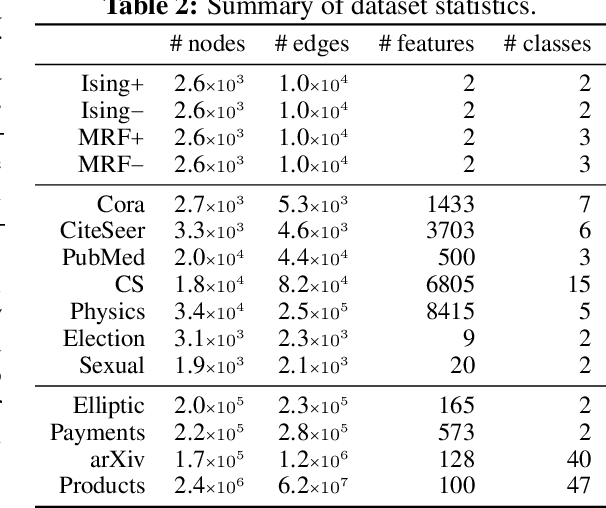
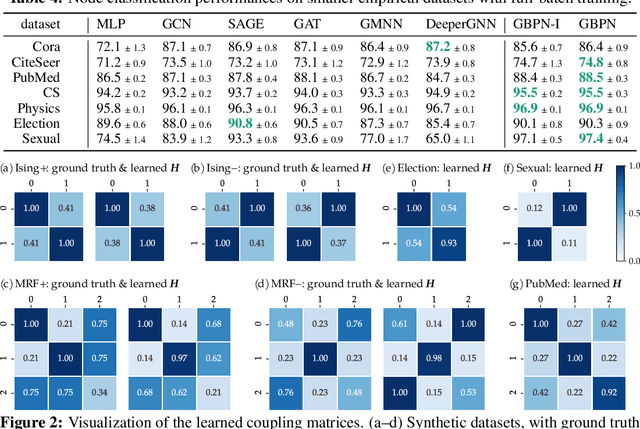

With the wide-spread availability of complex relational data, semi-supervised node classification in graphs has become a central machine learning problem. Graph neural networks are a recent class of easy-to-train and accurate methods for this problem that map the features in the neighborhood of a node to its label, but they ignore label correlation during inference and their predictions are difficult to interpret. On the other hand, collective classification is a traditional approach based on interpretable graphical models that explicitly model label correlations. Here, we introduce a model that combines the advantages of these two approaches, where we compute the marginal probabilities in a conditional random field, similar to collective classification, and the potentials in the random field are learned through end-to-end training, akin to graph neural networks. In our model, potentials on each node only depend on that node's features, and edge potentials are learned via a coupling matrix. This structure enables simple training with interpretable parameters, scales to large networks, naturally incorporates training labels at inference, and is often more accurate than related approaches. Our approach can be viewed as either an interpretable message-passing graph neural network or a collective classification method with higher capacity and modernized training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge