Fast Matrix Square Roots with Applications to Gaussian Processes and Bayesian Optimization
Paper and Code
Jun 19, 2020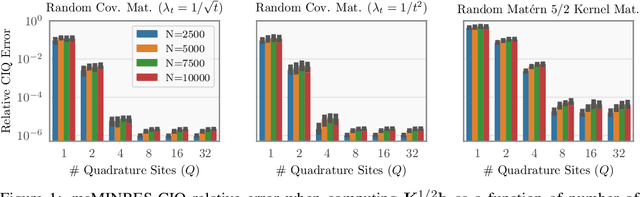
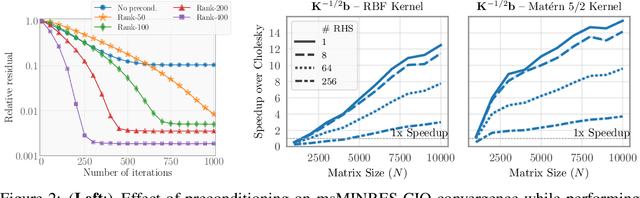
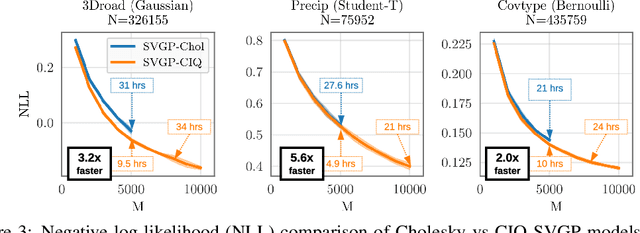

Matrix square roots and their inverses arise frequently in machine learning, e.g., when sampling from high-dimensional Gaussians $\mathcal{N}(\mathbf 0, \mathbf K)$ or whitening a vector $\mathbf b$ against covariance matrix $\mathbf K$. While existing methods typically require $O(N^3)$ computation, we introduce a highly-efficient quadratic-time algorithm for computing $\mathbf K^{1/2} \mathbf b$, $\mathbf K^{-1/2} \mathbf b$, and their derivatives through matrix-vector multiplication (MVMs). Our method combines Krylov subspace methods with a rational approximation and typically achieves $4$ decimal places of accuracy with fewer than $100$ MVMs. Moreover, the backward pass requires little additional computation. We demonstrate our method's applicability on matrices as large as $50,\!000 \times 50,\!000$ - well beyond traditional methods - with little approximation error. Applying this increased scalability to variational Gaussian processes, Bayesian optimization, and Gibbs sampling results in more powerful models with higher accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge