Reparameterized Variational Rejection Sampling

Traditional approaches to variational inference rely on parametric families of variational distributions, with the choice of family playing a critical role in determining the accuracy of the resulting posterior approximation. Simple mean-field families often lead to poor approximations, while rich families of distributions like normalizing flows can be difficult to optimize and usually do not incorporate the known structure of the target distribution due to their black-box nature. To expand the space of flexible variational families, we revisit Variational Rejection Sampling (VRS) [Grover et al., 2018], which combines a parametric proposal distribution with rejection sampling to define a rich non-parametric family of distributions that explicitly utilizes the known target distribution. By introducing a low-variance reparameterized gradient estimator for the parameters of the proposal distribution, we make VRS an attractive inference strategy for models with continuous latent variables. We argue theoretically and demonstrate empirically that the resulting method--Reparameterized Variational Rejection Sampling (RVRS)--offers an attractive trade-off between computational cost and inference fidelity. In experiments we show that our method performs well in practice and that it is well-suited for black-box inference, especially for models with local latent variables.

Bayesian Variable Selection in a Million Dimensions

Bayesian variable selection is a powerful tool for data analysis, as it offers a principled method for variable selection that accounts for prior information and uncertainty. However, wider adoption of Bayesian variable selection has been hampered by computational challenges, especially in difficult regimes with a large number of covariates P or non-conjugate likelihoods. To scale to the large P regime we introduce an efficient MCMC scheme whose cost per iteration is sublinear in P. In addition we show how this scheme can be extended to generalized linear models for count data, which are prevalent in biology, ecology, economics, and beyond. In particular we design efficient algorithms for variable selection in binomial and negative binomial regression, which includes logistic regression as a special case. In experiments we demonstrate the effectiveness of our methods, including on cancer and maize genomic data.

Surrogate Likelihoods for Variational Annealed Importance Sampling

Variational inference is a powerful paradigm for approximate Bayesian inference with a number of appealing properties, including support for model learning and data subsampling. By contrast MCMC methods like Hamiltonian Monte Carlo do not share these properties but remain attractive since, contrary to parametric methods, MCMC is asymptotically unbiased. For these reasons researchers have sought to combine the strengths of both classes of algorithms, with recent approaches coming closer to realizing this vision in practice. However, supporting data subsampling in these hybrid methods can be a challenge, a shortcoming that we address by introducing a surrogate likelihood that can be learned jointly with other variational parameters. We argue theoretically that the resulting algorithm permits the user to make an intuitive trade-off between inference fidelity and computational cost. In an extensive empirical comparison we show that our method performs well in practice and that it is well-suited for black-box inference in probabilistic programming frameworks.

Fast Bayesian Variable Selection in Binomial and Negative Binomial Regression

Bayesian variable selection is a powerful tool for data analysis, as it offers a principled method for variable selection that accounts for prior information and uncertainty. However, wider adoption of Bayesian variable selection has been hampered by computational challenges, especially in difficult regimes with a large number of covariates or non-conjugate likelihoods. Generalized linear models for count data, which are prevalent in biology, ecology, economics, and beyond, represent an important special case. Here we introduce an efficient MCMC scheme for variable selection in binomial and negative binomial regression that exploits Tempered Gibbs Sampling (Zanella and Roberts, 2019) and that includes logistic regression as a special case. In experiments we demonstrate the effectiveness of our approach, including on cancer data with seventeen thousand covariates.

Scalable Cross Validation Losses for Gaussian Process Models

We introduce a simple and scalable method for training Gaussian process (GP) models that exploits cross-validation and nearest neighbor truncation. To accommodate binary and multi-class classification we leverage P\`olya-Gamma auxiliary variables and variational inference. In an extensive empirical comparison with a number of alternative methods for scalable GP regression and classification, we find that our method offers fast training and excellent predictive performance. We argue that the good predictive performance can be traced to the non-parametric nature of the resulting predictive distributions as well as to the cross-validation loss, which provides robustness against model mis-specification.

High-Dimensional Bayesian Optimization with Sparse Axis-Aligned Subspaces

Bayesian optimization (BO) is a powerful paradigm for efficient optimization of black-box objective functions. High-dimensional BO presents a particular challenge, in part because the curse of dimensionality makes it difficult to define as well as do inference over a suitable class of surrogate models. We argue that Gaussian process surrogate models defined on sparse axis-aligned subspaces offer an attractive compromise between flexibility and parsimony. We demonstrate that our approach, which relies on Hamiltonian Monte Carlo for inference, can rapidly identify sparse subspaces relevant to modeling the unknown objective function, enabling sample-efficient high-dimensional BO. In an extensive suite of experiments comparing to existing methods for high-dimensional BO we demonstrate that our algorithm, Sparse Axis-Aligned Subspace BO (SAASBO), achieves excellent performance on several synthetic and real-world problems without the need to set problem-specific hyperparameters.

Fast Matrix Square Roots with Applications to Gaussian Processes and Bayesian Optimization

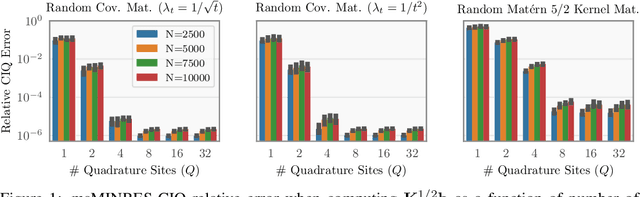
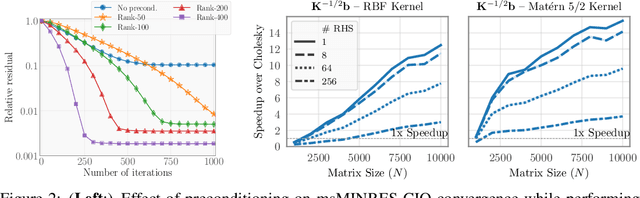
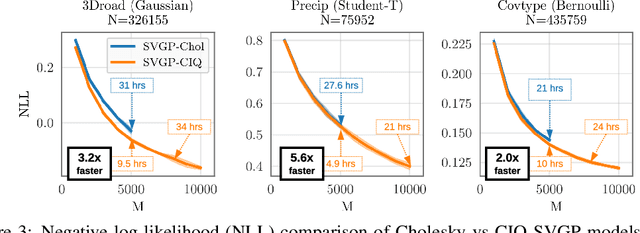
Matrix square roots and their inverses arise frequently in machine learning, e.g., when sampling from high-dimensional Gaussians $\mathcal{N}(\mathbf 0, \mathbf K)$ or whitening a vector $\mathbf b$ against covariance matrix $\mathbf K$. While existing methods typically require $O(N^3)$ computation, we introduce a highly-efficient quadratic-time algorithm for computing $\mathbf K^{1/2} \mathbf b$, $\mathbf K^{-1/2} \mathbf b$, and their derivatives through matrix-vector multiplication (MVMs). Our method combines Krylov subspace methods with a rational approximation and typically achieves $4$ decimal places of accuracy with fewer than $100$ MVMs. Moreover, the backward pass requires little additional computation. We demonstrate our method's applicability on matrices as large as $50,\!000 \times 50,\!000$ - well beyond traditional methods - with little approximation error. Applying this increased scalability to variational Gaussian processes, Bayesian optimization, and Gibbs sampling results in more powerful models with higher accuracy.

Deep Sigma Point Processes

We introduce Deep Sigma Point Processes, a class of parametric models inspired by the compositional structure of Deep Gaussian Processes (DGPs). Deep Sigma Point Processes (DSPPs) retain many of the attractive features of (variational) DGPs, including mini-batch training and predictive uncertainty that is controlled by kernel basis functions. Importantly, since DSPPs admit a simple maximum likelihood inference procedure, the resulting predictive distributions are not degraded by any posterior approximations. In an extensive empirical comparison on univariate and multivariate regression tasks we find that the resulting predictive distributions are significantly better calibrated than those obtained with other probabilistic methods for scalable regression, including variational DGPs--often by as much as a nat per datapoint.

Composable Effects for Flexible and Accelerated Probabilistic Programming in NumPyro

NumPyro is a lightweight library that provides an alternate NumPy backend to the Pyro probabilistic programming language with the same modeling interface, language primitives and effect handling abstractions. Effect handlers allow Pyro's modeling API to be extended to NumPyro despite its being built atop a fundamentally different JAX-based functional backend. In this work, we demonstrate the power of composing Pyro's effect handlers with the program transformations that enable hardware acceleration, automatic differentiation, and vectorization in JAX. In particular, NumPyro provides an iterative formulation of the No-U-Turn Sampler (NUTS) that can be end-to-end JIT compiled, yielding an implementation that is much faster than existing alternatives in both the small and large dataset regimes.

A Unified Stochastic Gradient Approach to Designing Bayesian-Optimal Experiments

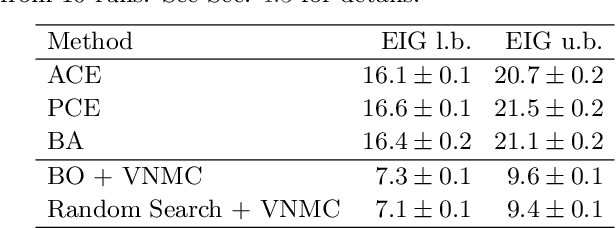
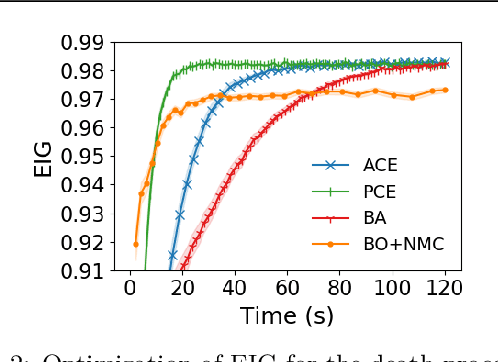
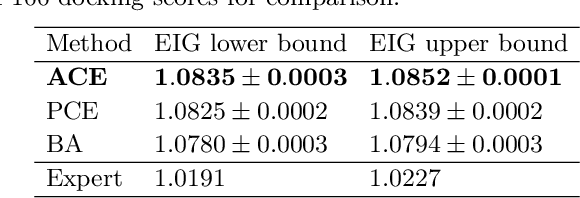
We introduce a fully stochastic gradient based approach to Bayesian optimal experimental design (BOED). This is achieved through the use of variational lower bounds on the expected information gain (EIG) of an experiment that can be simultaneously optimized with respect to both the variational and design parameters. This allows the design process to be carried out through a single unified stochastic gradient ascent procedure, in contrast to existing approaches that typically construct an EIG estimator on a pointwise basis, before passing this estimator to a separate optimizer. We show that this, in turn, leads to more efficient BOED schemes and provide a number of a different variational objectives suited to different settings. Furthermore, we show that our gradient-based approaches are able to provide effective design optimization in substantially higher dimensional settings than existing approaches.