Block Diffusion: Interpolating Between Autoregressive and Diffusion Language Models

Diffusion language models offer unique benefits over autoregressive models due to their potential for parallelized generation and controllability, yet they lag in likelihood modeling and are limited to fixed-length generation. In this work, we introduce a class of block diffusion language models that interpolate between discrete denoising diffusion and autoregressive models. Block diffusion overcomes key limitations of both approaches by supporting flexible-length generation and improving inference efficiency with KV caching and parallel token sampling. We propose a recipe for building effective block diffusion models that includes an efficient training algorithm, estimators of gradient variance, and data-driven noise schedules to minimize the variance. Block diffusion sets a new state-of-the-art performance among diffusion models on language modeling benchmarks and enables generation of arbitrary-length sequences. We provide the code, along with the model weights and blog post on the project page: https://m-arriola.com/bd3lms/

Simple Guidance Mechanisms for Discrete Diffusion Models

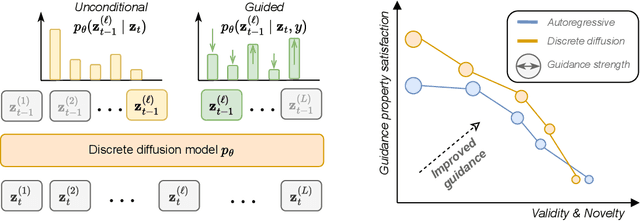
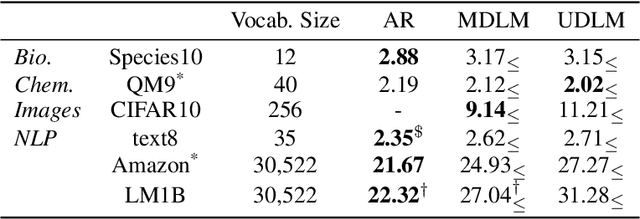
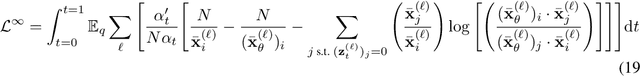
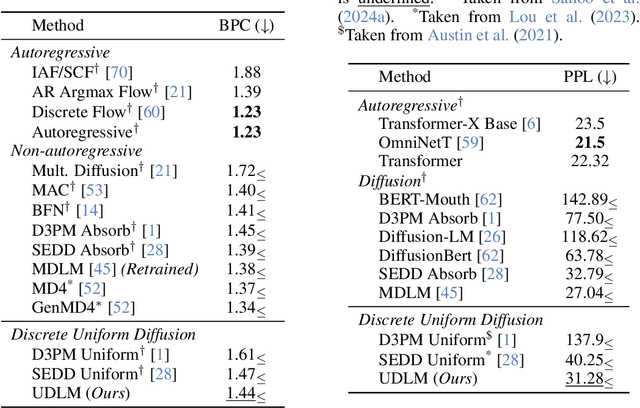
Diffusion models for continuous data gained widespread adoption owing to their high quality generation and control mechanisms. However, controllable diffusion on discrete data faces challenges given that continuous guidance methods do not directly apply to discrete diffusion. Here, we provide a straightforward derivation of classifier-free and classifier-based guidance for discrete diffusion, as well as a new class of diffusion models that leverage uniform noise and that are more guidable because they can continuously edit their outputs. We improve the quality of these models with a novel continuous-time variational lower bound that yields state-of-the-art performance, especially in settings involving guidance or fast generation. Empirically, we demonstrate that our guidance mechanisms combined with uniform noise diffusion improve controllable generation relative to autoregressive and diffusion baselines on several discrete data domains, including genomic sequences, small molecule design, and discretized image generation.

Simple and Effective Masked Diffusion Language Models

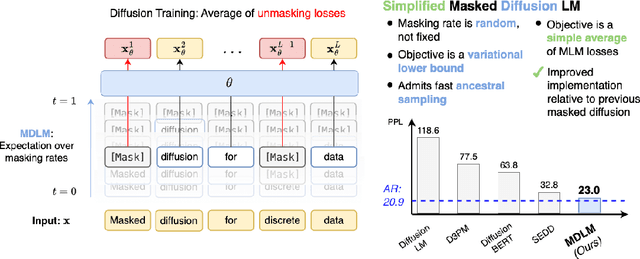
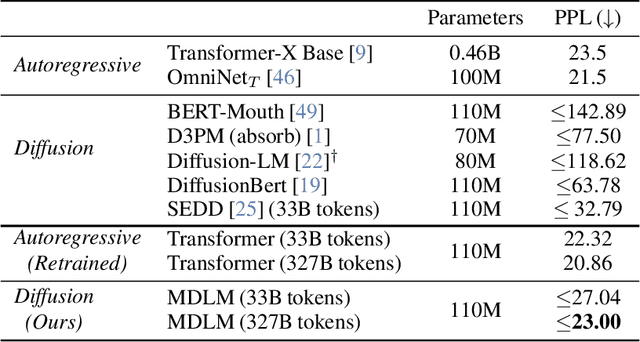
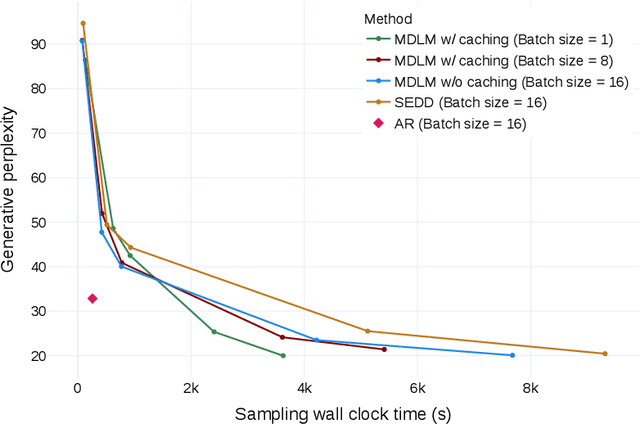
While diffusion models excel at generating high-quality images, prior work reports a significant performance gap between diffusion and autoregressive (AR) methods in language modeling. In this work, we show that simple masked discrete diffusion is more performant than previously thought. We apply an effective training recipe that improves the performance of masked diffusion models and derive a simplified, Rao-Blackwellized objective that results in additional improvements. Our objective has a simple form -- it is a mixture of classical masked language modeling losses -- and can be used to train encoder-only language models that admit efficient samplers, including ones that can generate arbitrary lengths of text semi-autoregressively like a traditional language model. On language modeling benchmarks, a range of masked diffusion models trained with modern engineering practices achieves a new state-of-the-art among diffusion models, and approaches AR perplexity. We release our code at: https://github.com/kuleshov-group/mdlm

Diffusion Models With Learned Adaptive Noise

Diffusion models have gained traction as powerful algorithms for synthesizing high-quality images. Central to these algorithms is the diffusion process, which maps data to noise according to equations inspired by thermodynamics and can significantly impact performance. A widely held assumption is that the ELBO objective of a diffusion model is invariant to the noise process (Kingma et al.,2021). In this work, we dispel this assumption -- we propose multivariate learned adaptive noise (MuLAN), a learned diffusion process that applies Gaussian noise at different rates across an image. Our method consists of three components -- a multivariate noise schedule, instance-conditional diffusion, and auxiliary variables -- which ensure that the learning objective is no longer invariant to the choice of the noise schedule as in previous works. Our work is grounded in Bayesian inference and casts the learned diffusion process as an approximate variational posterior that yields a tighter lower bound on marginal likelihood. Empirically, MuLAN sets a new state-of-the-art in density estimation on CIFAR-10 and ImageNet compared to classical diffusion. Code is available at https://github.com/s-sahoo/MuLAN

Gradient Backpropagation Through Combinatorial Algorithms: Identity with Projection Works

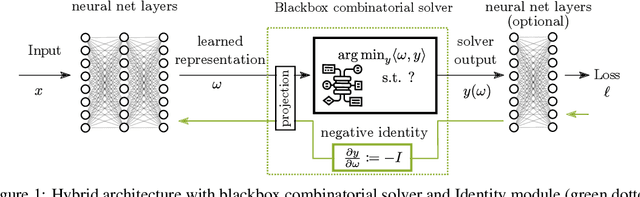
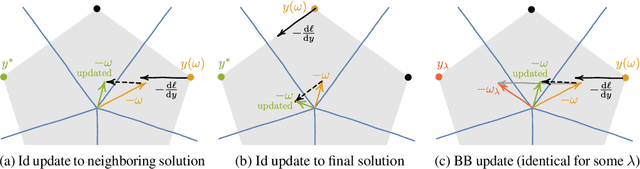
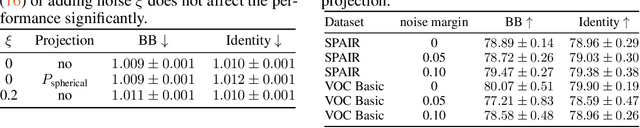
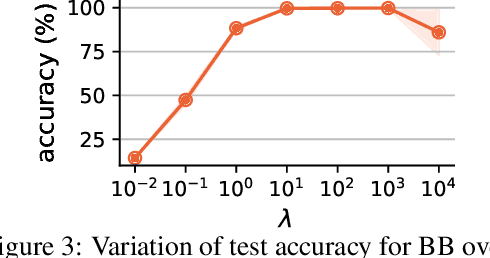
Embedding discrete solvers as differentiable layers has given modern deep learning architectures combinatorial expressivity and discrete reasoning capabilities. The derivative of these solvers is zero or undefined, therefore a meaningful replacement is crucial for effective gradient-based learning. Prior works rely on smoothing the solver with input perturbations, relaxing the solver to continuous problems, or interpolating the loss landscape with techniques that typically require additional solver calls, introduce extra hyper-parameters or compromise performance. We propose a principled approach to exploit the geometry of the discrete solution space to treat the solver as a negative identity on the backward pass and further provide a theoretical justification. Our experiments demonstrate that such a straightforward hyper-parameter-free approach is on-par with or outperforms previous more complex methods on numerous experiments such as Traveling Salesman Problem, Shortest Path, Deep Graph Matching, and backpropagating through discrete samplers. Furthermore, we substitute the previously proposed problem-specific and label-dependent margin by a generic regularization procedure that prevents cost collapse and increases robustness.

Scaling Symbolic Methods using Gradients for Neural Model Explanation

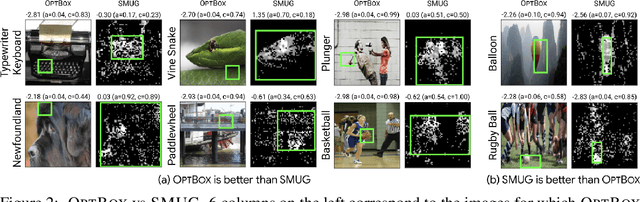
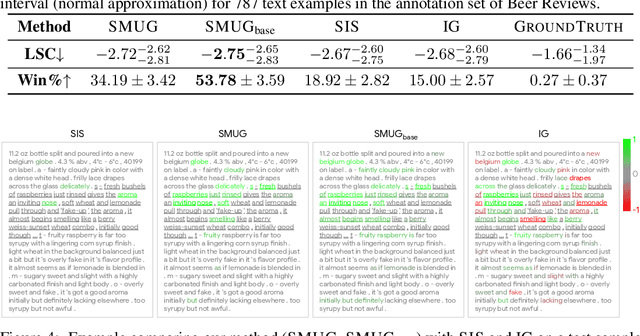
Symbolic techniques based on Satisfiability Modulo Theory (SMT) solvers have been proposed for analyzing and verifying neural network properties, but their usage has been fairly limited owing to their poor scalability with larger networks. In this work, we propose a technique for combining gradient-based methods with symbolic techniques to scale such analyses and demonstrate its application for model explanation. In particular, we apply this technique to identify minimal regions in an input that are most relevant for a neural network's prediction. Our approach uses gradient information (based on Integrated Gradients) to focus on a subset of neurons in the first layer, which allows our technique to scale to large networks. The corresponding SMT constraints encode the minimal input mask discovery problem such that after masking the input, the activations of the selected neurons are still above a threshold. After solving for the minimal masks, our approach scores the mask regions to generate a relative ordering of the features within the mask. This produces a saliency map which explains "where a model is looking" when making a prediction. We evaluate our technique on three datasets - MNIST, ImageNet, and Beer Reviews, and demonstrate both quantitatively and qualitatively that the regions generated by our approach are sparser and achieve higher saliency scores compared to the gradient-based methods alone.