Rishabh Singh
Microsoft Research, Redmond
The Llama 4 Herd: Architecture, Training, Evaluation, and Deployment Notes
Jan 15, 2026Abstract:This document consolidates publicly reported technical details about Metas Llama 4 model family. It summarizes (i) released variants (Scout and Maverick) and the broader herd context including the previewed Behemoth teacher model, (ii) architectural characteristics beyond a high-level MoE description covering routed/shared-expert structure, early-fusion multimodality, and long-context design elements reported for Scout (iRoPE and length generalization strategies), (iii) training disclosures spanning pre-training, mid-training for long-context extension, and post-training methodology (lightweight SFT, online RL, and lightweight DPO) as described in release materials, (iv) developer-reported benchmark results for both base and instruction-tuned checkpoints, and (v) practical deployment constraints observed across major serving environments, including provider-specific context limits and quantization packaging. The manuscript also summarizes licensing obligations relevant to redistribution and derivative naming, and reviews publicly described safeguards and evaluation practices. The goal is to provide a compact technical reference for researchers and practitioners who need precise, source-backed facts about Llama 4.
SWE-RL: Advancing LLM Reasoning via Reinforcement Learning on Open Software Evolution
Feb 25, 2025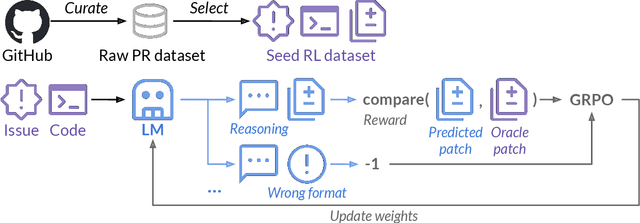


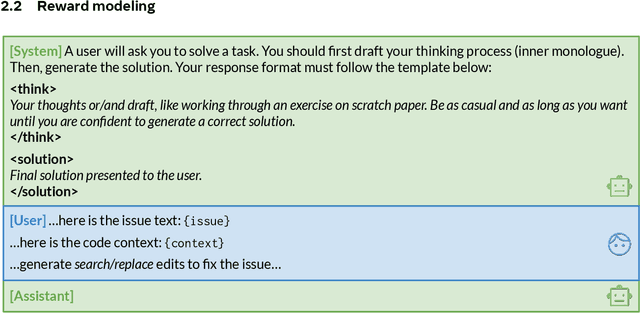
Abstract:The recent DeepSeek-R1 release has demonstrated the immense potential of reinforcement learning (RL) in enhancing the general reasoning capabilities of large language models (LLMs). While DeepSeek-R1 and other follow-up work primarily focus on applying RL to competitive coding and math problems, this paper introduces SWE-RL, the first approach to scale RL-based LLM reasoning for real-world software engineering. Leveraging a lightweight rule-based reward (e.g., the similarity score between ground-truth and LLM-generated solutions), SWE-RL enables LLMs to autonomously recover a developer's reasoning processes and solutions by learning from extensive open-source software evolution data -- the record of a software's entire lifecycle, including its code snapshots, code changes, and events such as issues and pull requests. Trained on top of Llama 3, our resulting reasoning model, Llama3-SWE-RL-70B, achieves a 41.0% solve rate on SWE-bench Verified -- a human-verified collection of real-world GitHub issues. To our knowledge, this is the best performance reported for medium-sized (<100B) LLMs to date, even comparable to leading proprietary LLMs like GPT-4o. Surprisingly, despite performing RL solely on software evolution data, Llama3-SWE-RL has even emerged with generalized reasoning skills. For example, it shows improved results on five out-of-domain tasks, namely, function coding, library use, code reasoning, mathematics, and general language understanding, whereas a supervised-finetuning baseline even leads to performance degradation on average. Overall, SWE-RL opens up a new direction to improve the reasoning capabilities of LLMs through reinforcement learning on massive software engineering data.
EdgeFlowNet: 100FPS@1W Dense Optical Flow For Tiny Mobile Robots
Nov 21, 2024



Abstract:Optical flow estimation is a critical task for tiny mobile robotics to enable safe and accurate navigation, obstacle avoidance, and other functionalities. However, optical flow estimation on tiny robots is challenging due to limited onboard sensing and computation capabilities. In this paper, we propose EdgeFlowNet , a high-speed, low-latency dense optical flow approach for tiny autonomous mobile robots by harnessing the power of edge computing. We demonstrate the efficacy of our approach by deploying EdgeFlowNet on a tiny quadrotor to perform static obstacle avoidance, flight through unknown gaps and dynamic obstacle dodging. EdgeFlowNet is about 20 faster than the previous state-of-the-art approaches while improving accuracy by over 20% and using only 1.08W of power enabling advanced autonomy on palm-sized tiny mobile robots.
Quantifying Model Uncertainty for Semantic Segmentation using Operators in the RKHS
Nov 03, 2022



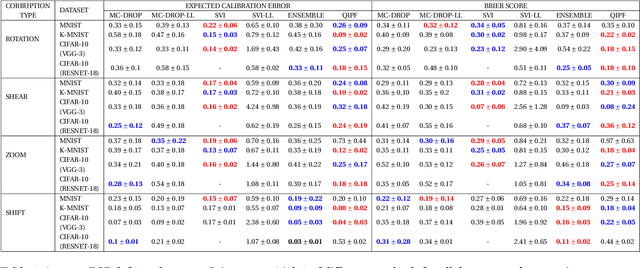
Abstract:Deep learning models for semantic segmentation are prone to poor performance in real-world applications due to the highly challenging nature of the task. Model uncertainty quantification (UQ) is one way to address this issue of lack of model trustworthiness by enabling the practitioner to know how much to trust a segmentation output. Current UQ methods in this application domain are mainly restricted to Bayesian based methods which are computationally expensive and are only able to extract central moments of uncertainty thereby limiting the quality of their uncertainty estimates. We present a simple framework for high-resolution predictive uncertainty quantification of semantic segmentation models that leverages a multi-moment functional definition of uncertainty associated with the model's feature space in the reproducing kernel Hilbert space (RKHS). The multiple uncertainty functionals extracted from this framework are defined by the local density dynamics of the model's feature space and hence automatically align themselves at the tail-regions of the intrinsic probability density function of the feature space (where uncertainty is the highest) in such a way that the successively higher order moments quantify the more uncertain regions. This leads to a significantly more accurate view of model uncertainty than conventional Bayesian methods. Moreover, the extraction of such moments is done in a single-shot computation making it much faster than Bayesian and ensemble approaches (that involve a high number of forward stochastic passes of the model to quantify its uncertainty). We demonstrate these advantages through experimental evaluations of our framework implemented over four different state-of-the-art model architectures that are trained and evaluated on two benchmark road-scene segmentation datasets (Camvid and Cityscapes).
Robust Dependence Measure using RKHS based Uncertainty Moments and Optimal Transport
Nov 03, 2022



Abstract:Reliable measurement of dependence between variables is essential in many applications of statistics and machine learning. Current approaches for dependence estimation, especially density-based approaches, lack in precision, robustness and/or interpretability (in terms of the type of dependence being estimated). We propose a two-step approach for dependence quantification between random variables: 1) We first decompose the probability density functions (PDF) of the variables involved in terms of multiple local moments of uncertainty that systematically and precisely identify the different regions of the PDF (with special emphasis on the tail-regions). 2) We then compute an optimal transport map to measure the geometric similarity between the corresponding sets of decomposed local uncertainty moments of the variables. Dependence is then determined by the degree of one-to-one correspondence between the respective uncertainty moments of the variables in the optimal transport map. We utilize a recently introduced Gaussian reproducing kernel Hilbert space (RKHS) based framework for multi-moment uncertainty decomposition of the variables. Being based on the Gaussian RKHS, our approach is robust towards outliers and monotone transformations of data, while the multiple moments of uncertainty provide high resolution and interpretability of the type of dependence being quantified. We support these claims through some preliminary results using simulated data.
Quantifying Model Predictive Uncertainty with Perturbation Theory
Sep 22, 2021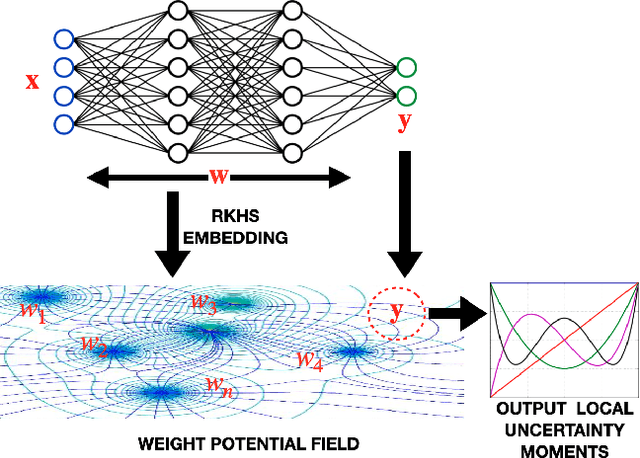
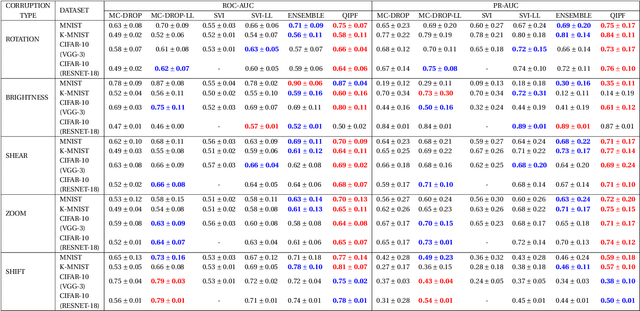
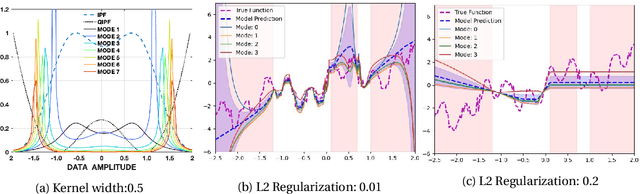
Abstract:We propose a framework for predictive uncertainty quantification of a neural network that replaces the conventional Bayesian notion of weight probability density function (PDF) with a physics based potential field representation of the model weights in a Gaussian reproducing kernel Hilbert space (RKHS) embedding. This allows us to use perturbation theory from quantum physics to formulate a moment decomposition problem over the model weight-output relationship. The extracted moments reveal successive degrees of regularization of the weight potential field around the local neighborhood of the model output. Such localized moments represent well the PDF tails and provide significantly greater accuracy of the model's predictive uncertainty than the central moments characterized by Bayesian and ensemble methods or their variants. We show that this consequently leads to a better ability to detect false model predictions of test data that has undergone a covariate shift away from the training PDF learned by the model. We evaluate our approach against baseline uncertainty quantification methods on several benchmark datasets that are corrupted using common distortion techniques. Our approach provides fast model predictive uncertainty estimates with much greater precision and calibration.
Deep Geospatial Interpolation Networks
Aug 15, 2021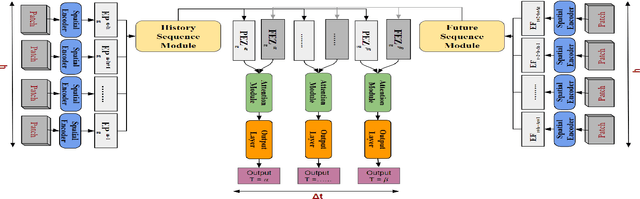
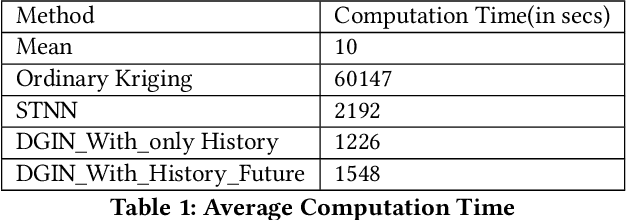
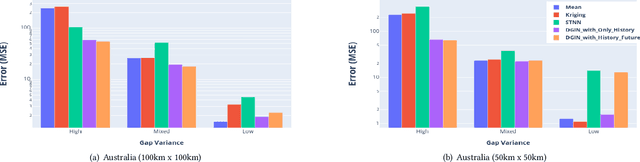
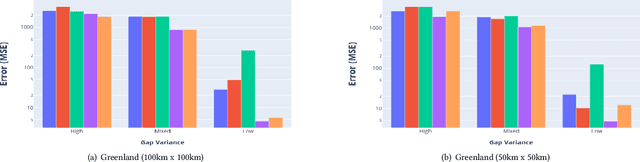
Abstract:Interpolation in Spatio-temporal data has applications in various domains such as climate, transportation, and mining. Spatio-Temporal interpolation is highly challenging due to the complex spatial and temporal relationships. However, traditional techniques such as Kriging suffer from high running time and poor performance on data that exhibit high variance across space and time dimensions. To this end, we propose a novel deep neural network called as Deep Geospatial Interpolation Network(DGIN), which incorporates both spatial and temporal relationships and has significantly lower training time. DGIN consists of three major components: Spatial Encoder to capture the spatial dependencies, Sequential module to incorporate the temporal dynamics, and an Attention block to learn the importance of the temporal neighborhood around the gap. We evaluate DGIN on the MODIS reflectance dataset from two different regions. Our experimental results indicate that DGIN has two advantages: (a) it outperforms alternative approaches (has lower MSE with p-value < 0.01) and, (b) it has significantly low execution time than Kriging.
SpreadsheetCoder: Formula Prediction from Semi-structured Context
Jun 26, 2021



Abstract:Spreadsheet formula prediction has been an important program synthesis problem with many real-world applications. Previous works typically utilize input-output examples as the specification for spreadsheet formula synthesis, where each input-output pair simulates a separate row in the spreadsheet. However, this formulation does not fully capture the rich context in real-world spreadsheets. First, spreadsheet data entries are organized as tables, thus rows and columns are not necessarily independent from each other. In addition, many spreadsheet tables include headers, which provide high-level descriptions of the cell data. However, previous synthesis approaches do not consider headers as part of the specification. In this work, we present the first approach for synthesizing spreadsheet formulas from tabular context, which includes both headers and semi-structured tabular data. In particular, we propose SpreadsheetCoder, a BERT-based model architecture to represent the tabular context in both row-based and column-based formats. We train our model on a large dataset of spreadsheets, and demonstrate that SpreadsheetCoder achieves top-1 prediction accuracy of 42.51%, which is a considerable improvement over baselines that do not employ rich tabular context. Compared to the rule-based system, SpreadsheetCoder assists 82% more users in composing formulas on Google Sheets.
Image to Image Translation : Generating maps from satellite images
May 19, 2021


Abstract:Generation of maps from satellite images is conventionally done by a range of tools. Maps became an important part of life whose conversion from satellite images may be a bit expensive but Generative models can pander to this challenge. These models aims at finding the patterns between the input and output image. Image to image translation is employed to convert satellite image to corresponding map. Different techniques for image to image translations like Generative adversarial network, Conditional adversarial networks and Co-Variational Auto encoders are used to generate the corresponding human-readable maps for that region, which takes a satellite image at a given zoom level as its input. We are training our model on Conditional Generative Adversarial Network which comprises of Generator model which which generates fake images while the discriminator tries to classify the image as real or fake and both these models are trained synchronously in adversarial manner where both try to fool each other and result in enhancing model performance.
A Kernel Framework to Quantify a Model's Local Predictive Uncertainty under Data Distributional Shifts
Mar 02, 2021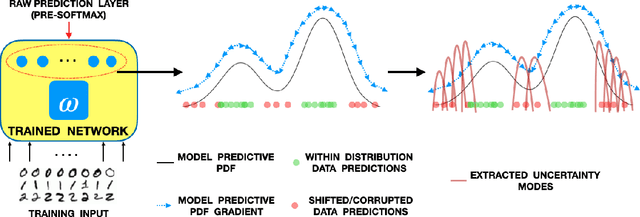
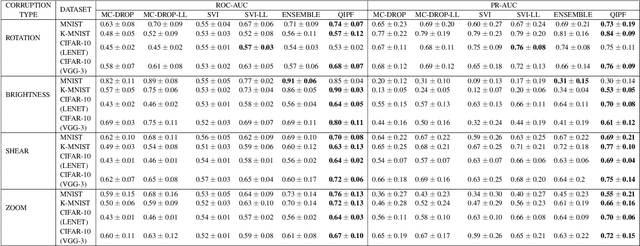
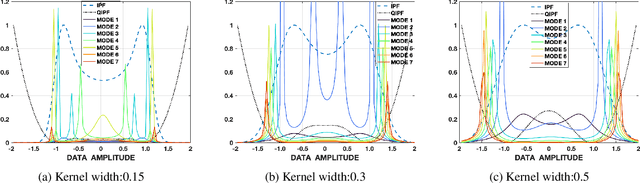
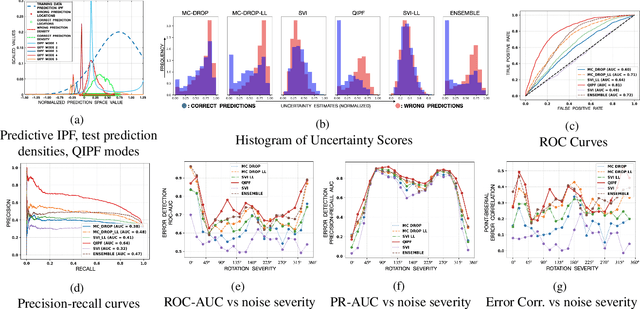
Abstract:Traditional Bayesian approaches for model uncertainty quantification rely on notoriously difficult processes of marginalization over each network parameter to estimate its probability density function (PDF). Our hypothesis is that internal layer outputs of a trained neural network contain all of the information related to both its mapping function (quantified by its weights) as well as the input data distribution. We therefore propose a framework for predictive uncertainty quantification of a trained neural network that explicitly estimates the PDF of its raw prediction space (before activation), p(y'|x,w), which we refer to as the model PDF, in a Gaussian reproducing kernel Hilbert space (RKHS). The Gaussian RKHS provides a localized density estimate of p(y'|x,w), which further enables us to utilize gradient based formulations of quantum physics to decompose the model PDF in terms of multiple local uncertainty moments that provide much greater resolution of the PDF than the central moments characterized by Bayesian methods. This provides the framework with a better ability to detect distributional shifts in test data away from the training data PDF learned by the model. We evaluate the framework against existing uncertainty quantification methods on benchmark datasets that have been corrupted using common perturbation techniques. The kernel framework is observed to provide model uncertainty estimates with much greater precision based on the ability to detect model prediction errors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge