Vít Musil
LSP-DETR: Efficient and Scalable Nuclei Segmentation in Whole Slide Images
Jan 06, 2026Abstract:Precise and scalable instance segmentation of cell nuclei is essential for computational pathology, yet gigapixel Whole-Slide Images pose major computational challenges. Existing approaches rely on patch-based processing and costly post-processing for instance separation, sacrificing context and efficiency. We introduce LSP-DETR (Local Star Polygon DEtection TRansformer), a fully end-to-end framework that uses a lightweight transformer with linear complexity to process substantially larger images without additional computational cost. Nuclei are represented as star-convex polygons, and a novel radial distance loss function allows the segmentation of overlapping nuclei to emerge naturally, without requiring explicit overlap annotations or handcrafted post-processing. Evaluations on PanNuke and MoNuSeg show strong generalization across tissues and state-of-the-art efficiency, with LSP-DETR being over five times faster than the next-fastest leading method. Code and models are available at https://github.com/RationAI/lsp-detr.
Beyond Occlusion: In Search for Near Real-Time Explainability of CNN-Based Prostate Cancer Classification
Dec 19, 2025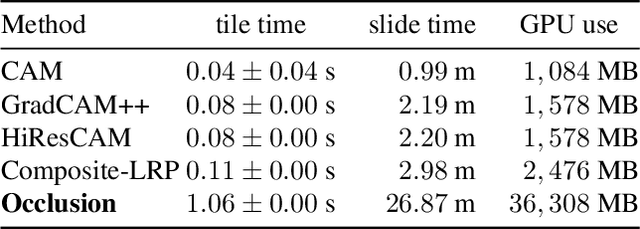
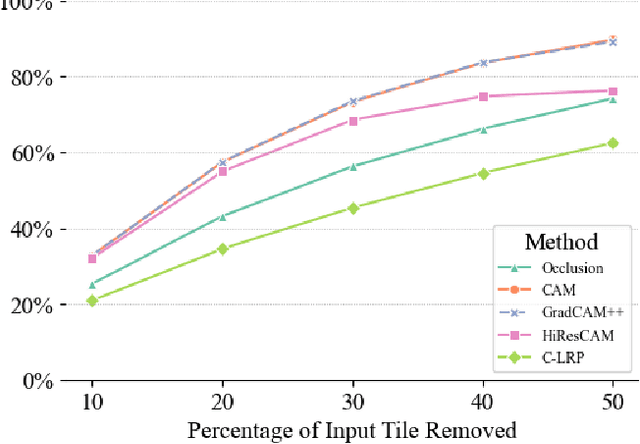
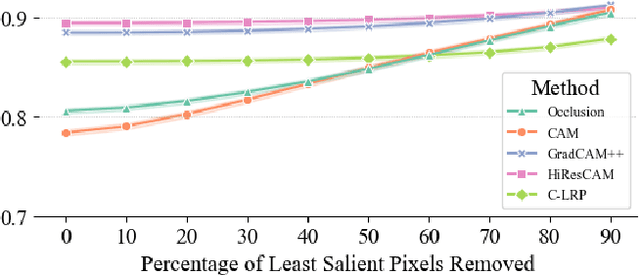
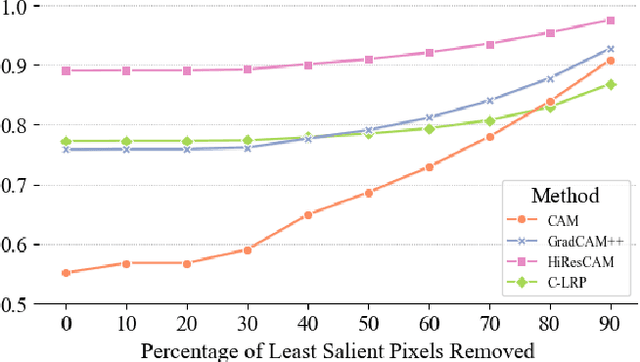
Abstract:Deep neural networks are starting to show their worth in critical applications such as assisted cancer diagnosis. However, for their outputs to get accepted in practice, the results they provide should be explainable in a way easily understood by pathologists. A well-known and widely used explanation technique is occlusion, which, however, can take a long time to compute, thus slowing the development and interaction with pathologists. In this work, we set out to find a faster replacement for occlusion in a successful system for detecting prostate cancer. Since there is no established framework for comparing the performance of various explanation methods, we first identified suitable comparison criteria and selected corresponding metrics. Based on the results, we were able to choose a different explanation method, which cut the previously required explanation time at least by a factor of 10, without any negative impact on the quality of outputs. This speedup enables rapid iteration in model development and debugging and brings us closer to adopting AI-assisted prostate cancer detection in clinical settings. We propose that our approach to finding the replacement for occlusion can be used to evaluate candidate methods in other related applications.
Explaining Digital Pathology Models via Clustering Activations
Nov 18, 2025Abstract:We present a clustering-based explainability technique for digital pathology models based on convolutional neural networks. Unlike commonly used methods based on saliency maps, such as occlusion, GradCAM, or relevance propagation, which highlight regions that contribute the most to the prediction for a single slide, our method shows the global behaviour of the model under consideration, while also providing more fine-grained information. The result clusters can be visualised not only to understand the model, but also to increase confidence in its operation, leading to faster adoption in clinical practice. We also evaluate the performance of our technique on an existing model for detecting prostate cancer, demonstrating its usefulness.
Hard Contacts with Soft Gradients: Refining Differentiable Simulators for Learning and Control
Jun 17, 2025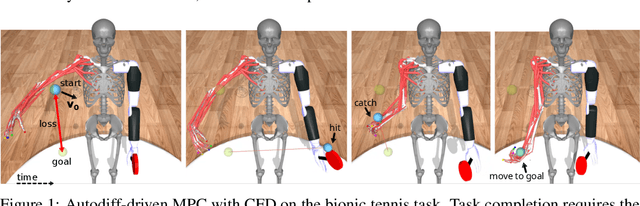
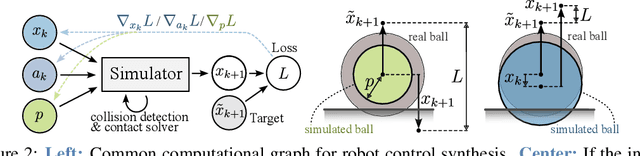
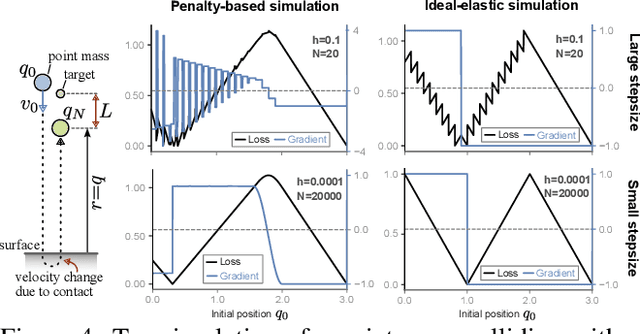
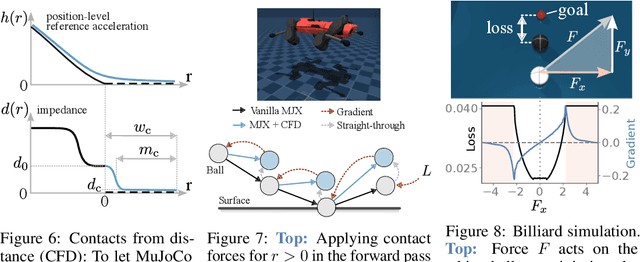
Abstract:Contact forces pose a major challenge for gradient-based optimization of robot dynamics as they introduce jumps in the system's velocities. Penalty-based simulators, such as MuJoCo, simplify gradient computation by softening the contact forces. However, realistically simulating hard contacts requires very stiff contact settings, which leads to incorrect gradients when using automatic differentiation. On the other hand, using non-stiff settings strongly increases the sim-to-real gap. We analyze the contact computation of penalty-based simulators to identify the causes of gradient errors. Then, we propose DiffMJX, which combines adaptive integration with MuJoCo XLA, to notably improve gradient quality in the presence of hard contacts. Finally, we address a key limitation of contact gradients: they vanish when objects do not touch. To overcome this, we introduce Contacts From Distance (CFD), a mechanism that enables the simulator to generate informative contact gradients even before objects are in contact. To preserve physical realism, we apply CFD only in the backward pass using a straight-through trick, allowing us to compute useful gradients without modifying the forward simulation.
Memory Assignment for Finite-Memory Strategies in Adversarial Patrolling Games
May 20, 2025Abstract:Adversarial Patrolling games form a subclass of Security games where a Defender moves between locations, guarding vulnerable targets. The main algorithmic problem is constructing a strategy for the Defender that minimizes the worst damage an Attacker can cause. We focus on the class of finite-memory (also known as regular) Defender's strategies that experimentally outperformed other competing classes. A finite-memory strategy can be seen as a positional strategy on a finite set of states. Each state consists of a pair of a location and a certain integer value--called memory. Existing algorithms improve the transitional probabilities between the states but require that the available memory size itself is assigned at each location manually. Choosing the right memory assignment is a well-known open and hard problem that hinders the usability of finite-memory strategies. We solve this issue by developing a general method that iteratively changes the memory assignment. Our algorithm can be used in connection with \emph{any} black-box strategy optimization tool. We evaluate our method on various experiments and show its robustness by solving instances of various patrolling models.
Multiple Mean-Payoff Optimization under Local Stability Constraints
Dec 17, 2024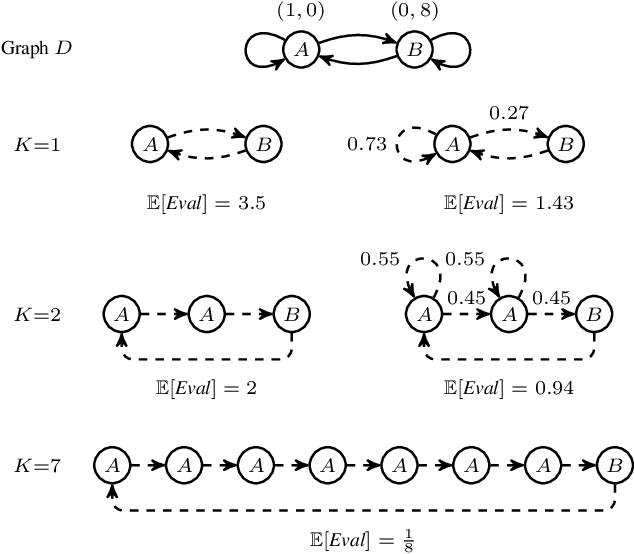
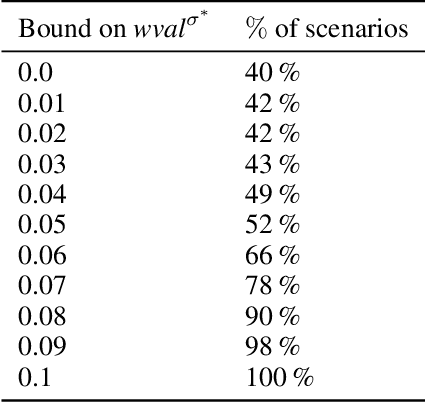
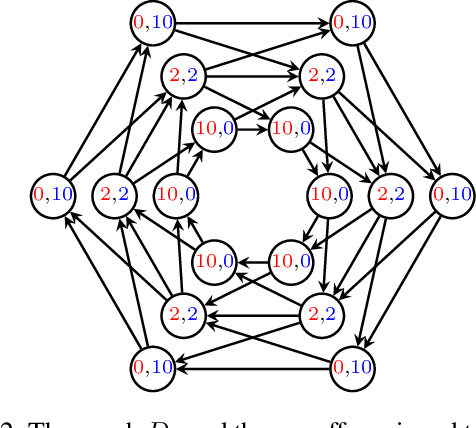
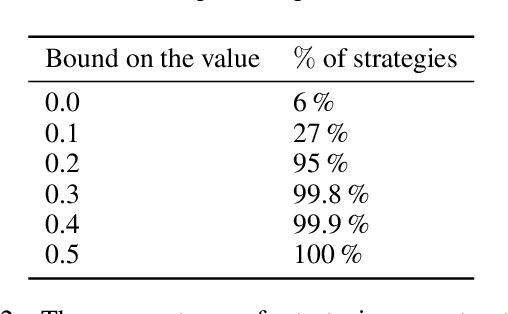
Abstract:The long-run average payoff per transition (mean payoff) is the main tool for specifying the performance and dependability properties of discrete systems. The problem of constructing a controller (strategy) simultaneously optimizing several mean payoffs has been deeply studied for stochastic and game-theoretic models. One common issue of the constructed controllers is the instability of the mean payoffs, measured by the deviations of the average rewards per transition computed in a finite "window" sliding along a run. Unfortunately, the problem of simultaneously optimizing the mean payoffs under local stability constraints is computationally hard, and the existing works do not provide a practically usable algorithm even for non-stochastic models such as two-player games. In this paper, we design and evaluate the first efficient and scalable solution to this problem applicable to Markov decision processes.
LPGD: A General Framework for Backpropagation through Embedded Optimization Layers
Jul 08, 2024Abstract:Embedding parameterized optimization problems as layers into machine learning architectures serves as a powerful inductive bias. Training such architectures with stochastic gradient descent requires care, as degenerate derivatives of the embedded optimization problem often render the gradients uninformative. We propose Lagrangian Proximal Gradient Descent (LPGD) a flexible framework for training architectures with embedded optimization layers that seamlessly integrates into automatic differentiation libraries. LPGD efficiently computes meaningful replacements of the degenerate optimization layer derivatives by re-running the forward solver oracle on a perturbed input. LPGD captures various previously proposed methods as special cases, while fostering deep links to traditional optimization methods. We theoretically analyze our method and demonstrate on historical and synthetic data that LPGD converges faster than gradient descent even in a differentiable setup.
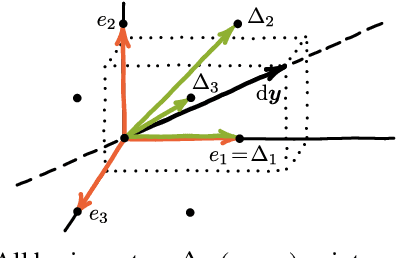
Gradient Backpropagation Through Combinatorial Algorithms: Identity with Projection Works
May 30, 2022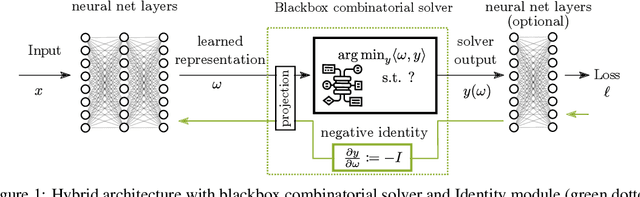
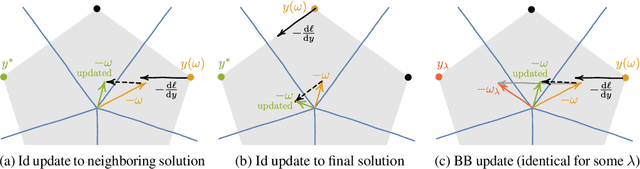
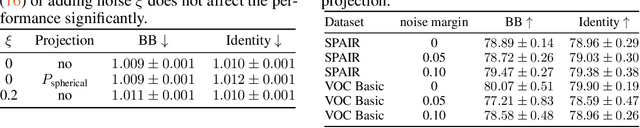
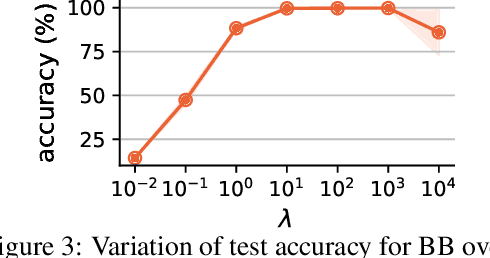
Abstract:Embedding discrete solvers as differentiable layers has given modern deep learning architectures combinatorial expressivity and discrete reasoning capabilities. The derivative of these solvers is zero or undefined, therefore a meaningful replacement is crucial for effective gradient-based learning. Prior works rely on smoothing the solver with input perturbations, relaxing the solver to continuous problems, or interpolating the loss landscape with techniques that typically require additional solver calls, introduce extra hyper-parameters or compromise performance. We propose a principled approach to exploit the geometry of the discrete solution space to treat the solver as a negative identity on the backward pass and further provide a theoretical justification. Our experiments demonstrate that such a straightforward hyper-parameter-free approach is on-par with or outperforms previous more complex methods on numerous experiments such as Traveling Salesman Problem, Shortest Path, Deep Graph Matching, and backpropagating through discrete samplers. Furthermore, we substitute the previously proposed problem-specific and label-dependent margin by a generic regularization procedure that prevents cost collapse and increases robustness.
General Optimization Framework for Recurrent Reachability Objectives
May 27, 2022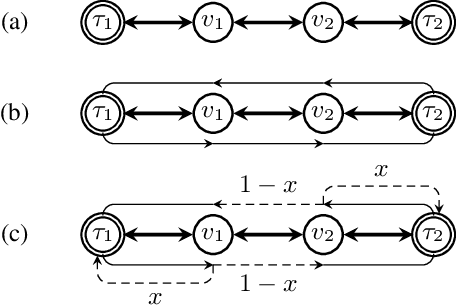
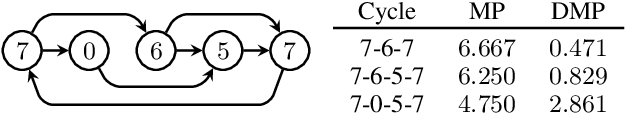
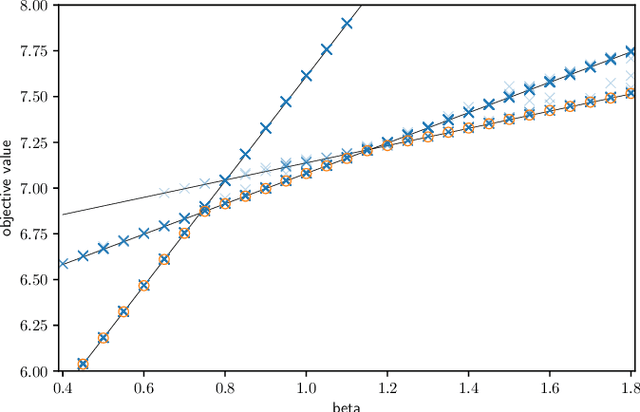
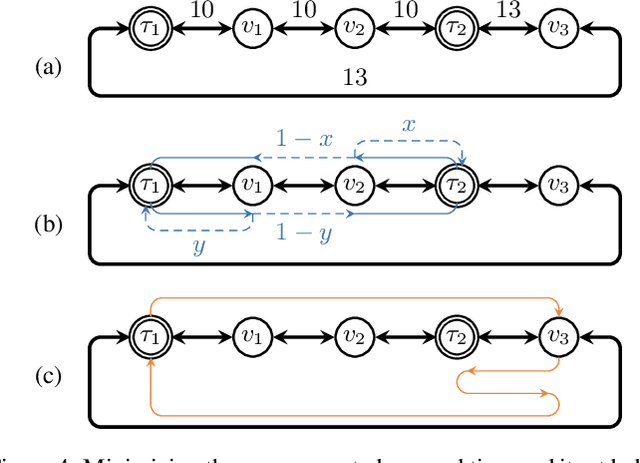
Abstract:We consider the mobile robot path planning problem for a class of recurrent reachability objectives. These objectives are parameterized by the expected time needed to visit one position from another, the expected square of this time, and also the frequency of moves between two neighboring locations. We design an efficient strategy synthesis algorithm for recurrent reachability objectives and demonstrate its functionality on non-trivial instances.
CombOptNet: Fit the Right NP-Hard Problem by Learning Integer Programming Constraints
May 05, 2021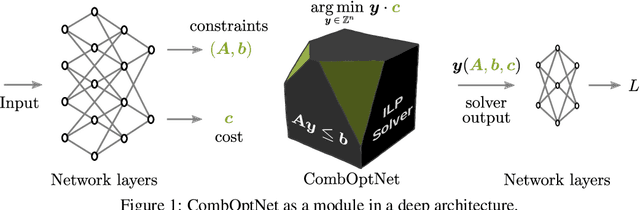
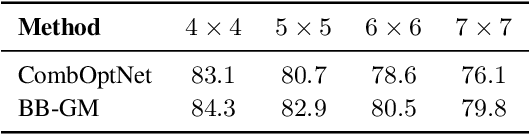

Abstract:Bridging logical and algorithmic reasoning with modern machine learning techniques is a fundamental challenge with potentially transformative impact. On the algorithmic side, many NP-hard problems can be expressed as integer programs, in which the constraints play the role of their "combinatorial specification". In this work, we aim to integrate integer programming solvers into neural network architectures as layers capable of learning both the cost terms and the constraints. The resulting end-to-end trainable architectures jointly extract features from raw data and solve a suitable (learned) combinatorial problem with state-of-the-art integer programming solvers. We demonstrate the potential of such layers with an extensive performance analysis on synthetic data and with a demonstration on a competitive computer vision keypoint matching benchmark.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge