Gradient Backpropagation Through Combinatorial Algorithms: Identity with Projection Works

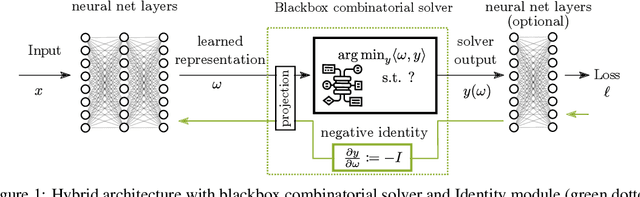
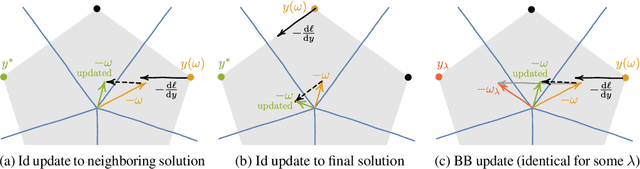
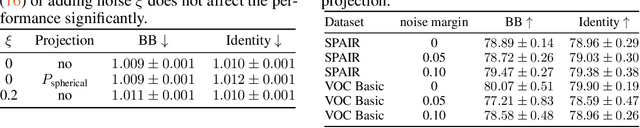
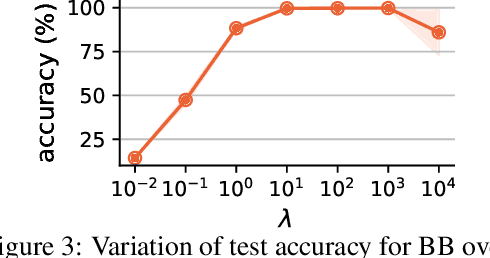
Embedding discrete solvers as differentiable layers has given modern deep learning architectures combinatorial expressivity and discrete reasoning capabilities. The derivative of these solvers is zero or undefined, therefore a meaningful replacement is crucial for effective gradient-based learning. Prior works rely on smoothing the solver with input perturbations, relaxing the solver to continuous problems, or interpolating the loss landscape with techniques that typically require additional solver calls, introduce extra hyper-parameters or compromise performance. We propose a principled approach to exploit the geometry of the discrete solution space to treat the solver as a negative identity on the backward pass and further provide a theoretical justification. Our experiments demonstrate that such a straightforward hyper-parameter-free approach is on-par with or outperforms previous more complex methods on numerous experiments such as Traveling Salesman Problem, Shortest Path, Deep Graph Matching, and backpropagating through discrete samplers. Furthermore, we substitute the previously proposed problem-specific and label-dependent margin by a generic regularization procedure that prevents cost collapse and increases robustness.