Multiple Mean-Payoff Optimization under Local Stability Constraints

The long-run average payoff per transition (mean payoff) is the main tool for specifying the performance and dependability properties of discrete systems. The problem of constructing a controller (strategy) simultaneously optimizing several mean payoffs has been deeply studied for stochastic and game-theoretic models. One common issue of the constructed controllers is the instability of the mean payoffs, measured by the deviations of the average rewards per transition computed in a finite "window" sliding along a run. Unfortunately, the problem of simultaneously optimizing the mean payoffs under local stability constraints is computationally hard, and the existing works do not provide a practically usable algorithm even for non-stochastic models such as two-player games. In this paper, we design and evaluate the first efficient and scalable solution to this problem applicable to Markov decision processes.

General Optimization Framework for Recurrent Reachability Objectives

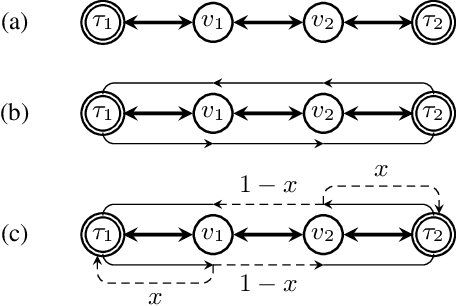
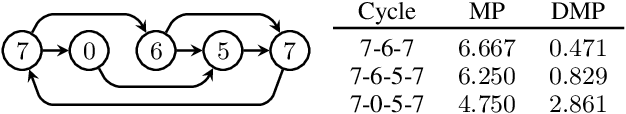
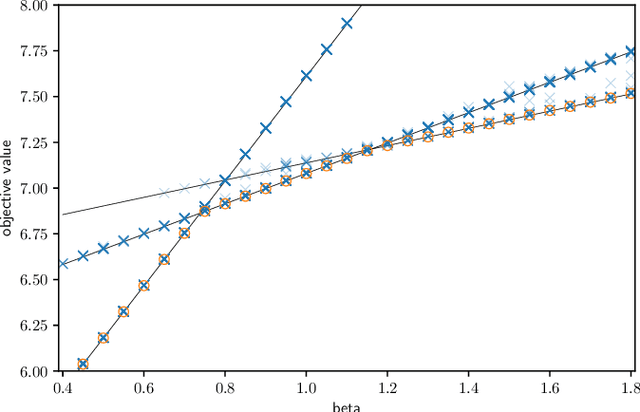
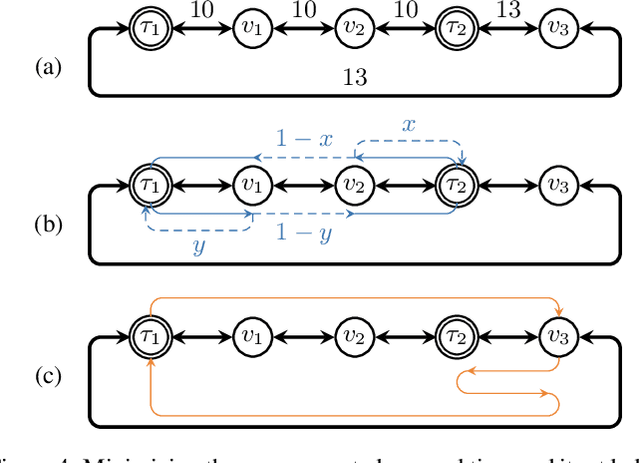
We consider the mobile robot path planning problem for a class of recurrent reachability objectives. These objectives are parameterized by the expected time needed to visit one position from another, the expected square of this time, and also the frequency of moves between two neighboring locations. We design an efficient strategy synthesis algorithm for recurrent reachability objectives and demonstrate its functionality on non-trivial instances.