A. René Geist
Hard Contacts with Soft Gradients: Refining Differentiable Simulators for Learning and Control
Jun 17, 2025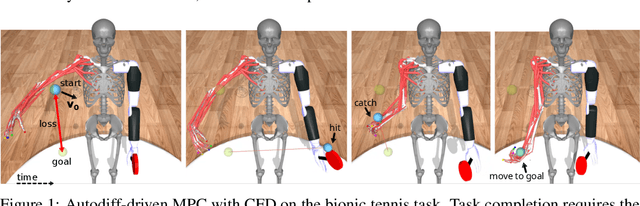
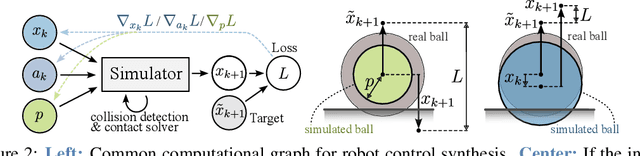
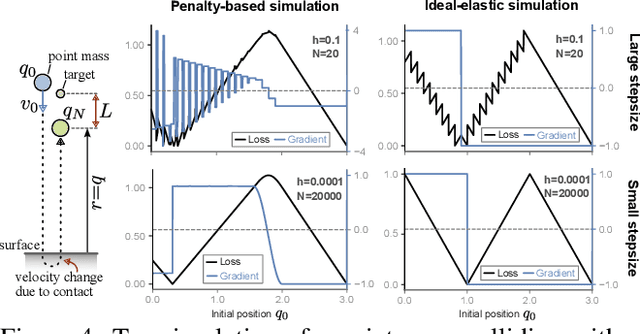
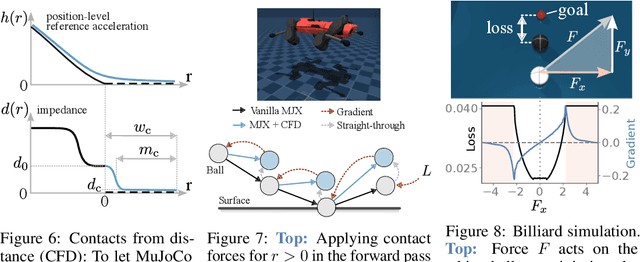
Abstract:Contact forces pose a major challenge for gradient-based optimization of robot dynamics as they introduce jumps in the system's velocities. Penalty-based simulators, such as MuJoCo, simplify gradient computation by softening the contact forces. However, realistically simulating hard contacts requires very stiff contact settings, which leads to incorrect gradients when using automatic differentiation. On the other hand, using non-stiff settings strongly increases the sim-to-real gap. We analyze the contact computation of penalty-based simulators to identify the causes of gradient errors. Then, we propose DiffMJX, which combines adaptive integration with MuJoCo XLA, to notably improve gradient quality in the presence of hard contacts. Finally, we address a key limitation of contact gradients: they vanish when objects do not touch. To overcome this, we introduce Contacts From Distance (CFD), a mechanism that enables the simulator to generate informative contact gradients even before objects are in contact. To preserve physical realism, we apply CFD only in the backward pass using a straight-through trick, allowing us to compute useful gradients without modifying the forward simulation.
A Smooth Analytical Formulation of Collision Detection and Rigid Body Dynamics With Contact
Mar 14, 2025Abstract:Generating intelligent robot behavior in contact-rich settings is a research problem where zeroth-order methods currently prevail. A major contributor to the success of such methods is their robustness in the face of non-smooth and discontinuous optimization landscapes that are characteristic of contact interactions, yet zeroth-order methods remain computationally inefficient. It is therefore desirable to develop methods for perception, planning and control in contact-rich settings that can achieve further efficiency by making use of first and second order information (i.e., gradients and Hessians). To facilitate this, we present a joint formulation of collision detection and contact modelling which, compared to existing differentiable simulation approaches, provides the following benefits: i) it results in forward and inverse dynamics that are entirely analytical (i.e. do not require solving optimization or root-finding problems with iterative methods) and smooth (i.e. twice differentiable), ii) it supports arbitrary collision geometries without needing a convex decomposition, and iii) its runtime is independent of the number of contacts. Through simulation experiments, we demonstrate the validity of the proposed formulation as a "physics for inference" that can facilitate future development of efficient methods to generate intelligent contact-rich behavior.
Learning deformable linear object dynamics from a single trajectory
Jul 03, 2024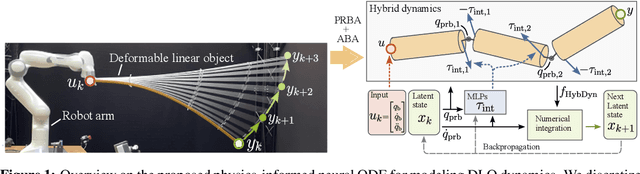
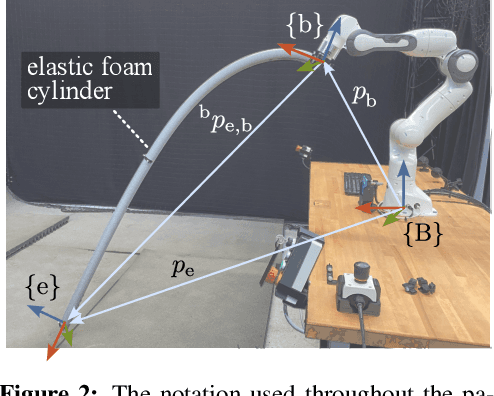


Abstract:The manipulation of deformable linear objects (DLOs) via model-based control requires an accurate and computationally efficient dynamics model. Yet, data-driven DLO dynamics models require large training data sets while their predictions often do not generalize, whereas physics-based models rely on good approximations of physical phenomena and often lack accuracy. To address these challenges, we propose a physics-informed neural ODE capable of predicting agile movements with significantly less data and hyper-parameter tuning. In particular, we model DLOs as serial chains of rigid bodies interconnected by passive elastic joints in which interaction forces are predicted by neural networks. The proposed model accurately predicts the motion of an robotically-actuated aluminium rod and an elastic foam cylinder after being trained on only thirty seconds of data. The project code and data are available at: \url{https://tinyurl.com/neuralprba}
Learning with 3D rotations, a hitchhiker's guide to SO
Apr 17, 2024



Abstract:Many settings in machine learning require the selection of a rotation representation. However, choosing a suitable representation from the many available options is challenging. This paper acts as a survey and guide through rotation representations. We walk through their properties that harm or benefit deep learning with gradient-based optimization. By consolidating insights from rotation-based learning, we provide a comprehensive overview of learning functions with rotation representations. We provide guidance on selecting representations based on whether rotations are in the model's input or output and whether the data primarily comprises small angles.
Finite element inspired networks: Learning physically-plausible deformable object dynamics from partial observations
Jul 16, 2023Abstract:The accurate simulation of deformable linear object (DLO) dynamics is challenging if the task at hand requires a human-interpretable and data-efficient model that also yields fast predictions. To arrive at such model, we draw inspiration from the rigid finite element method (R-FEM) and model a DLO as a serial chain of rigid bodies whose internal state is unrolled through time by a dynamics network. As this state is not observed directly, the dynamics network is trained jointly with a physics-informed encoder mapping observed motion variables to the body chain's state. To encourage that the state acquires a physically meaningful representation, we leverage the forward kinematics (FK) of the underlying R-FEM model as a decoder. We demonstrate in a robot experiment that this architecture - being termed "Finite element inspired network" - forms an easy to handle, yet capable DLO dynamics model yielding physically interpretable predictions from partial observations. The project code is available at: \url{https://tinyurl.com/fei-networks}
The Wheelbot: A Jumping Reaction Wheel Unicycle
Jul 14, 2022
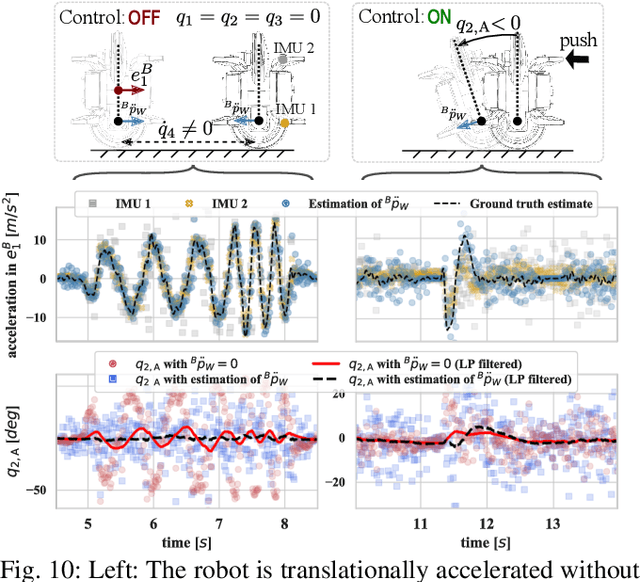
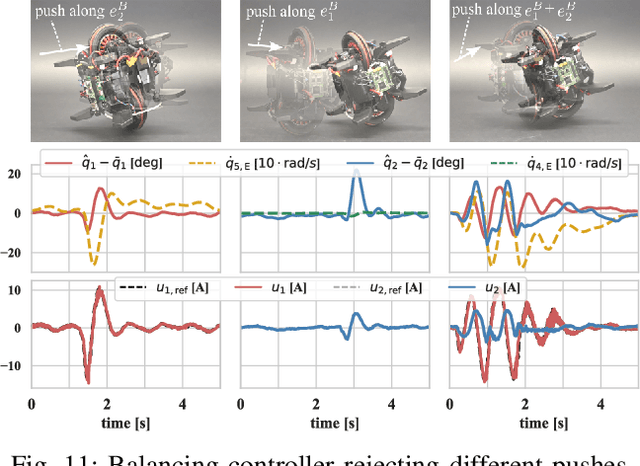

Abstract:Combining off-the-shelf components with 3Dprinting, the Wheelbot is a symmetric reaction wheel unicycle that can jump onto its wheels from any initial position. With non-holonomic and under-actuated dynamics, as well as two coupled unstable degrees of freedom, the Wheelbot provides a challenging platform for nonlinear and data-driven control research. This paper presents the Wheelbot's mechanical and electrical design, its estimation and control algorithms, as well as experiments demonstrating both self-erection and disturbance rejection while balancing.
Structured learning of rigid-body dynamics: A survey and unified view
Dec 11, 2020



Abstract:Accurate models of mechanical system dynamics are often critical for model-based control and reinforcement learning. Fully data-driven dynamics models promise to ease the process of modeling and analysis, but require considerable amounts of data for training and often do not generalize well to unseen parts of the state space. Combining data-driven modelling with prior analytical knowledge is an attractive alternative as the inclusion of structural knowledge into a regression model improves the model's data efficiency and physical integrity. In this article, we survey supervised regression models that combine rigid-body mechanics with data-driven modelling techniques. We analyze the different latent functions (such as kinetic energy or dissipative forces) and operators (such as differential operators and projection matrices) underlying common descriptions of rigid-body mechanics. Based on this analysis, we provide a unified view on the combination of data-driven regression models, such as neural networks and Gaussian processes, with analytical model priors. Further, we review and discuss key techniques for designing structured models such as automatic differentiation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge