Understanding and Detecting Convergence for Stochastic Gradient Descent with Momentum
Paper and Code
Aug 27, 2020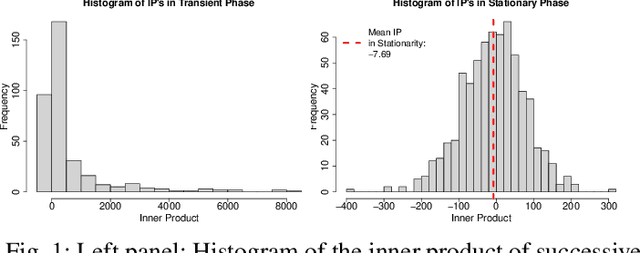
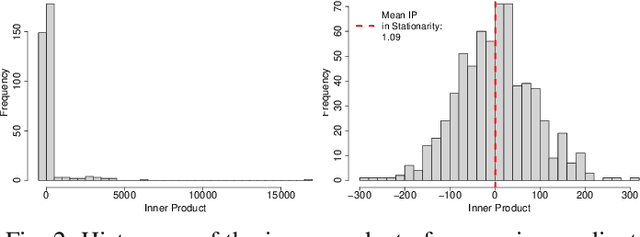
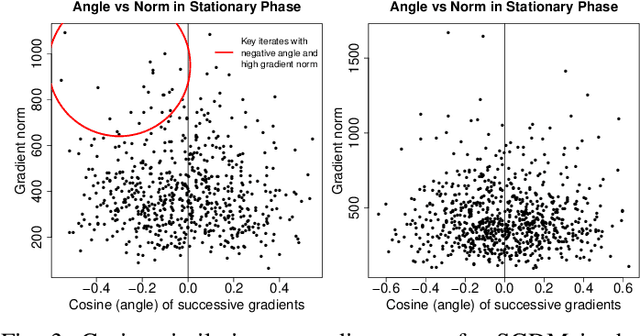
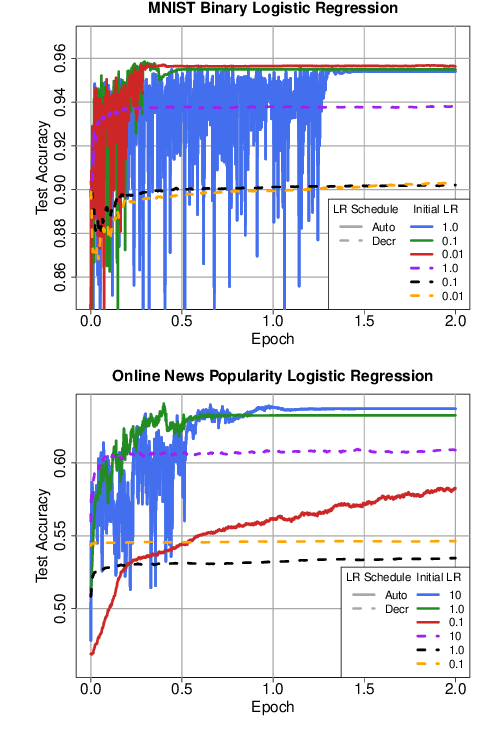
Convergence detection of iterative stochastic optimization methods is of great practical interest. This paper considers stochastic gradient descent (SGD) with a constant learning rate and momentum. We show that there exists a transient phase in which iterates move towards a region of interest, and a stationary phase in which iterates remain bounded in that region around a minimum point. We construct a statistical diagnostic test for convergence to the stationary phase using the inner product between successive gradients and demonstrate that the proposed diagnostic works well. We theoretically and empirically characterize how momentum can affect the test statistic of the diagnostic, and how the test statistic captures a relatively sparse signal within the gradients in convergence. Finally, we demonstrate an application to automatically tune the learning rate by reducing it each time stationarity is detected, and show the procedure is robust to mis-specified initial rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge