Panos Toulis
Stabilizing Temporal Difference Learning via Implicit Stochastic Approximation
May 02, 2025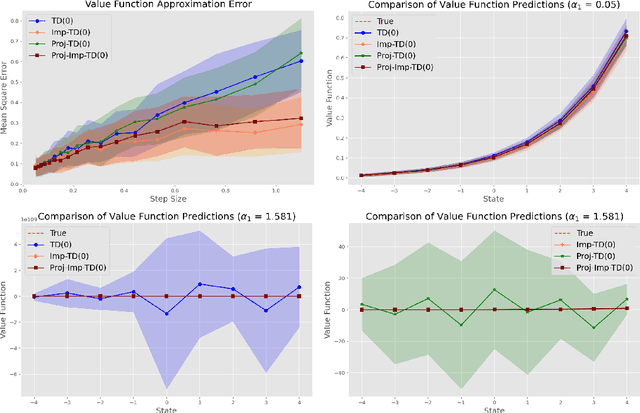
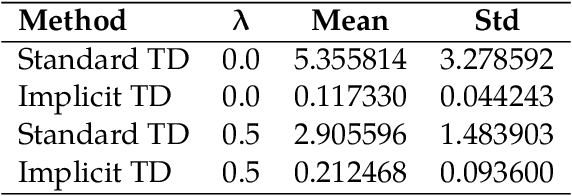
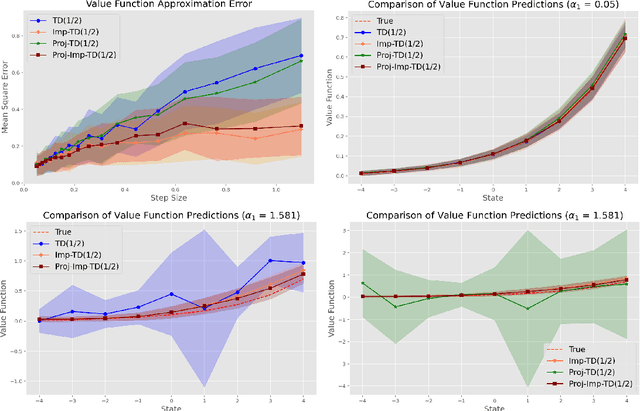
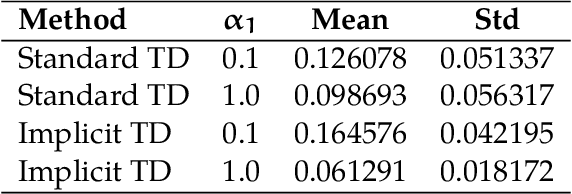
Abstract:Temporal Difference (TD) learning is a foundational algorithm in reinforcement learning (RL). For nearly forty years, TD learning has served as a workhorse for applied RL as well as a building block for more complex and specialized algorithms. However, despite its widespread use, it is not without drawbacks, the most prominent being its sensitivity to step size. A poor choice of step size can dramatically inflate the error of value estimates and slow convergence. Consequently, in practice, researchers must use trial and error in order to identify a suitable step size -- a process that can be tedious and time consuming. As an alternative, we propose implicit TD algorithms that reformulate TD updates into fixed-point equations. These updates are more stable and less sensitive to step size without sacrificing computational efficiency. Moreover, our theoretical analysis establishes asymptotic convergence guarantees and finite-time error bounds. Our results demonstrate their robustness and practicality for modern RL tasks, establishing implicit TD as a versatile tool for policy evaluation and value approximation.
ML-assisted Randomization Tests for Detecting Treatment Effects in A/B Experiments
Jan 13, 2025Abstract:Experimentation is widely utilized for causal inference and data-driven decision-making across disciplines. In an A/B experiment, for example, an online business randomizes two different treatments (e.g., website designs) to their customers and then aims to infer which treatment is better. In this paper, we construct randomization tests for complex treatment effects, including heterogeneity and interference. A key feature of our approach is the use of flexible machine learning (ML) models, where the test statistic is defined as the difference between the cross-validation errors from two ML models, one including the treatment variable and the other without it. This approach combines the predictive power of modern ML tools with the finite-sample validity of randomization procedures, enabling a robust and efficient way to detect complex treatment effects in experimental settings. We demonstrate this combined benefit both theoretically and empirically through applied examples.
Convergence and Stability of the Stochastic Proximal Point Algorithm with Momentum
Dec 03, 2021



Abstract:Stochastic gradient descent with momentum (SGDM) is the dominant algorithm in many optimization scenarios, including convex optimization instances and non-convex neural network training. Yet, in the stochastic setting, momentum interferes with gradient noise, often leading to specific step size and momentum choices in order to guarantee convergence, set aside acceleration. Proximal point methods, on the other hand, have gained much attention due to their numerical stability and elasticity against imperfect tuning. Their stochastic accelerated variants though have received limited attention: how momentum interacts with the stability of (stochastic) proximal point methods remains largely unstudied. To address this, we focus on the convergence and stability of the stochastic proximal point algorithm with momentum (SPPAM), and show that SPPAM allows a faster linear convergence rate compared to stochastic proximal point algorithm (SPPA) with a better contraction factor, under proper hyperparameter tuning. In terms of stability, we show that SPPAM depends on problem constants more favorably than SGDM, allowing a wider range of step size and momentum that lead to convergence.
Robust Inference for High-Dimensional Linear Models via Residual Randomization
Jun 14, 2021

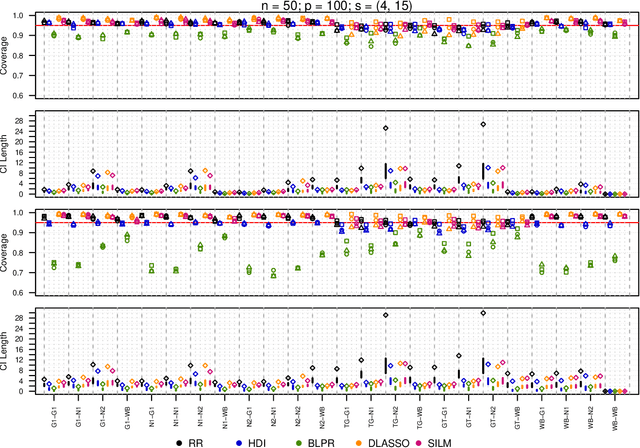
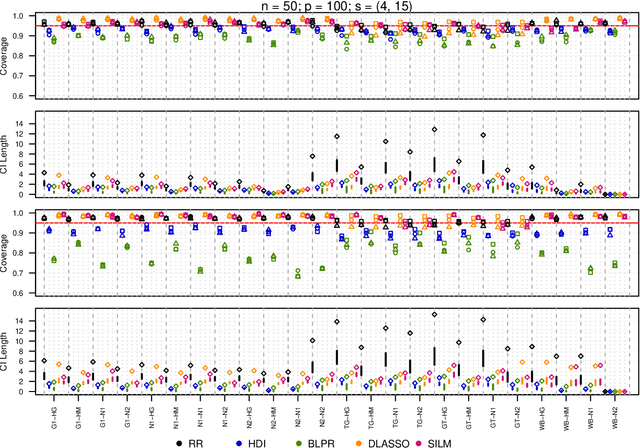
Abstract:We propose a residual randomization procedure designed for robust Lasso-based inference in the high-dimensional setting. Compared to earlier work that focuses on sub-Gaussian errors, the proposed procedure is designed to work robustly in settings that also include heavy-tailed covariates and errors. Moreover, our procedure can be valid under clustered errors, which is important in practice, but has been largely overlooked by earlier work. Through extensive simulations, we illustrate our method's wider range of applicability as suggested by theory. In particular, we show that our method outperforms state-of-art methods in challenging, yet more realistic, settings where the distribution of covariates is heavy-tailed or the sample size is small, while it remains competitive in standard, ``well behaved" settings previously studied in the literature.
Life After Bootstrap: Residual Randomization Inference in Regression Models
Aug 12, 2019



Abstract:We develop a randomization-based method for inference in regression models. The basis of inference is an invariance assumption on the regression errors, such as invariance to permutations or random signs. To test significance, the randomization method repeatedly calculates a suitable test statistic over transformations of the regression residuals according to the invariant. Inversion of the test can produce confidence intervals. We prove general conditions for asymptotic validity of this residual randomization test and illustrate in many models, including clustered errors with one-way or two-way clustering structure. We also show that finite-sample validity is possible under a suitable construction, and illustrate with an exact test for a case of the Behrens-Fisher problem. The proposed method offers four main advantages over the bootstrap: (1) it addresses the inference problem in a unified way, while bootstrap typically needs to be adapted to the task; (2) it can be more powerful by exploiting a richer and more flexible set of invariances than exchangeability; (3) it does not rely on asymptotic normality; and (4) it can be valid in finite samples. In extensive empirical evaluations, including high dimensional regression and autocorrelated errors, the proposed method performs favorably against many alternatives, including bootstrap variants and asymptotic robust error methods.
Stable Robbins-Monro approximations through stochastic proximal updates
Mar 05, 2018
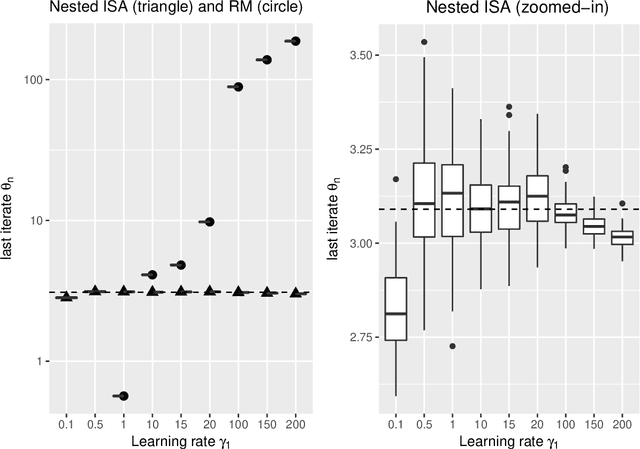
Abstract:The need for parameter estimation with massive data has reinvigorated interest in iterative estimation procedures. Stochastic approximations, such as stochastic gradient descent, are at the forefront of this recent development because they yield simple, generic, and extremely fast iterative estimation procedures. Such stochastic approximations, however, are often numerically unstable. As a consequence, current practice has turned to proximal operators, which can induce stable parameter updates within iterations. While the majority of classical iterative estimation procedures are subsumed by the framework of Robbins and Monro (1951), there is no such generalization for stochastic approximations with proximal updates. In this paper, we conceptualize a general stochastic approximation method with proximal updates. This method can be applied even in situations where the analytical form of the objective is not known, and so it generalizes many stochastic gradient procedures with proximal operators currently in use. Our theoretical analysis indicates that the proposed method has important stability benefits over the classical stochastic approximation method. Exact instantiations of the proposed method are challenging, but we show that approximate instantiations lead to procedures that are easy to implement, and still dominate classical procedures by achieving numerical stability without tradeoffs. This last advantage is akin to that seen in deterministic proximal optimization, where the framework is typically impossible to instantiate exactly, but where approximate instantiations lead to new optimization procedures that dominate classical ones.
Convergence diagnostics for stochastic gradient descent with constant step size
Feb 23, 2018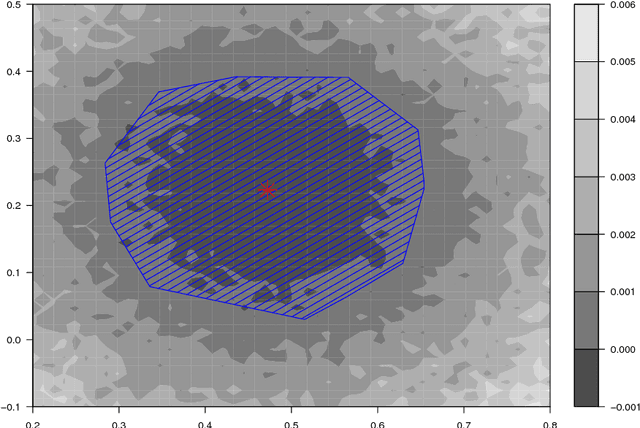
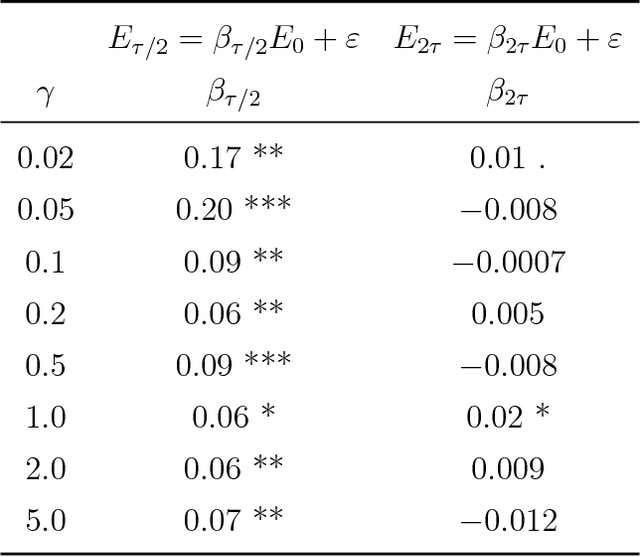
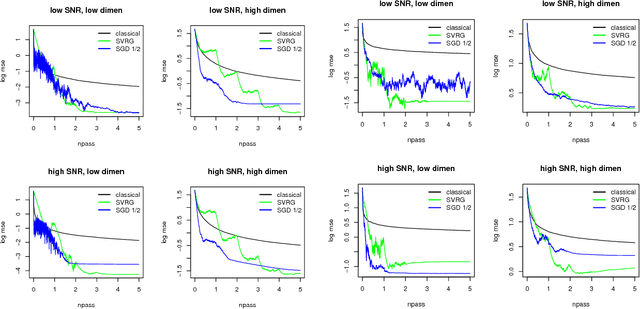
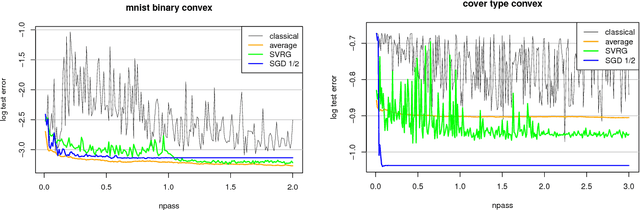
Abstract:Many iterative procedures in stochastic optimization exhibit a transient phase followed by a stationary phase. During the transient phase the procedure converges towards a region of interest, and during the stationary phase the procedure oscillates in that region, commonly around a single point. In this paper, we develop a statistical diagnostic test to detect such phase transition in the context of stochastic gradient descent with constant learning rate. We present theory and experiments suggesting that the region where the proposed diagnostic is activated coincides with the convergence region. For a class of loss functions, we derive a closed-form solution describing such region. Finally, we suggest an application to speed up convergence of stochastic gradient descent by halving the learning rate each time stationarity is detected. This leads to a new variant of stochastic gradient descent, which in many settings is comparable to state-of-art.
Asymptotic and finite-sample properties of estimators based on stochastic gradients
Sep 28, 2016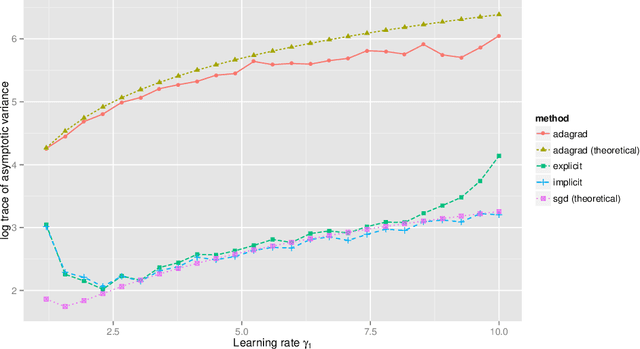

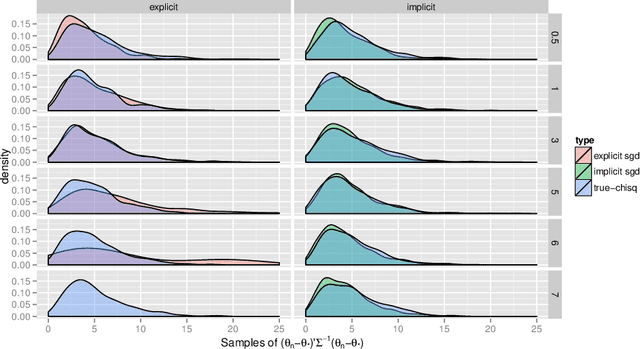
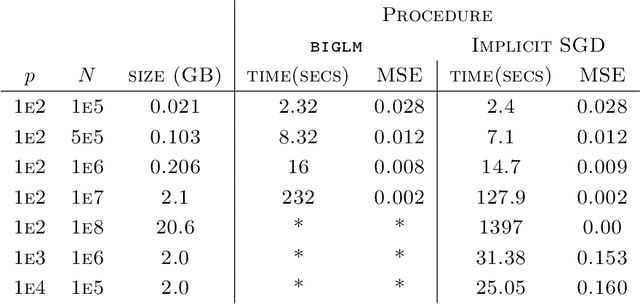
Abstract:Stochastic gradient descent procedures have gained popularity for parameter estimation from large data sets. However, their statistical properties are not well understood, in theory. And in practice, avoiding numerical instability requires careful tuning of key parameters. Here, we introduce implicit stochastic gradient descent procedures, which involve parameter updates that are implicitly defined. Intuitively, implicit updates shrink standard stochastic gradient descent updates. The amount of shrinkage depends on the observed Fisher information matrix, which does not need to be explicitly computed; thus, implicit procedures increase stability without increasing the computational burden. Our theoretical analysis provides the first full characterization of the asymptotic behavior of both standard and implicit stochastic gradient descent-based estimators, including finite-sample error bounds. Importantly, analytical expressions for the variances of these stochastic gradient-based estimators reveal their exact loss of efficiency. We also develop new algorithms to compute implicit stochastic gradient descent-based estimators for generalized linear models, Cox proportional hazards, M-estimators, in practice, and perform extensive experiments. Our results suggest that implicit stochastic gradient descent procedures are poised to become a workhorse for approximate inference from large data sets
Towards stability and optimality in stochastic gradient descent
Jun 07, 2016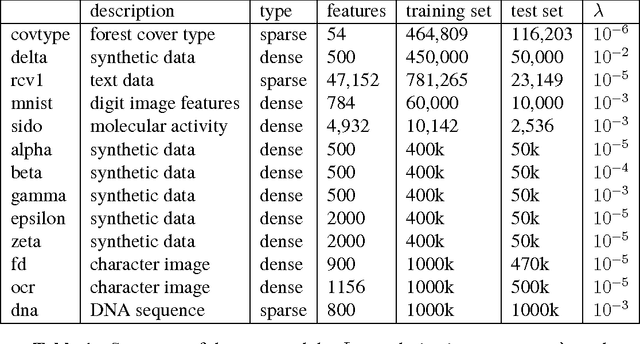
Abstract:Iterative procedures for parameter estimation based on stochastic gradient descent allow the estimation to scale to massive data sets. However, in both theory and practice, they suffer from numerical instability. Moreover, they are statistically inefficient as estimators of the true parameter value. To address these two issues, we propose a new iterative procedure termed averaged implicit SGD (AI-SGD). For statistical efficiency, AI-SGD employs averaging of the iterates, which achieves the optimal Cram\'{e}r-Rao bound under strong convexity, i.e., it is an optimal unbiased estimator of the true parameter value. For numerical stability, AI-SGD employs an implicit update at each iteration, which is related to proximal operators in optimization. In practice, AI-SGD achieves competitive performance with other state-of-the-art procedures. Furthermore, it is more stable than averaging procedures that do not employ proximal updates, and is simple to implement as it requires fewer tunable hyperparameters than procedures that do employ proximal updates.
Stochastic gradient descent methods for estimation with large data sets
Sep 22, 2015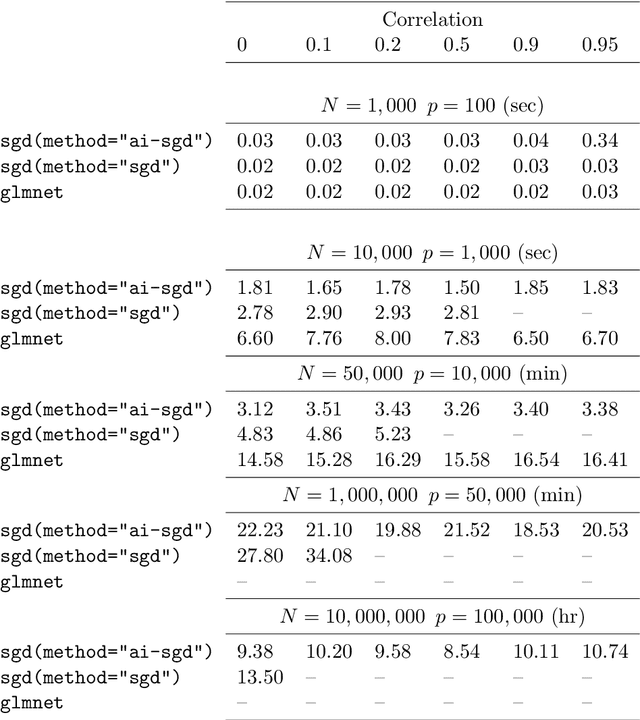
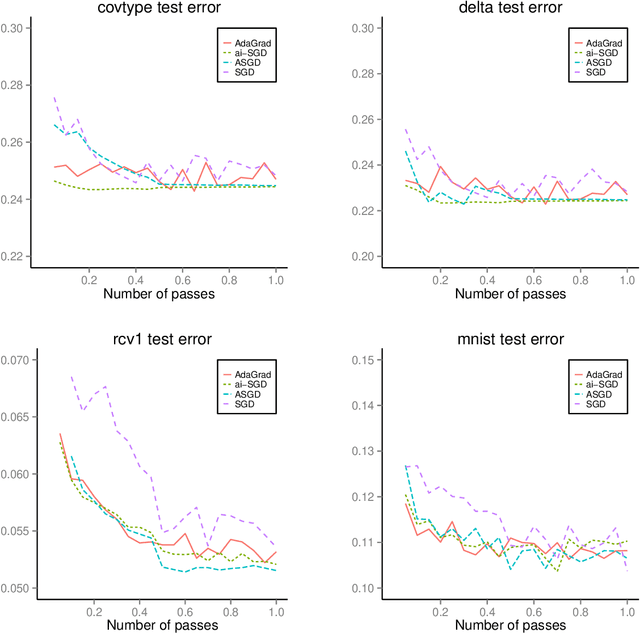
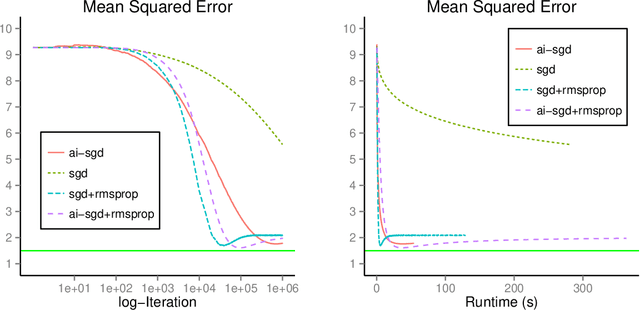
Abstract:We develop methods for parameter estimation in settings with large-scale data sets, where traditional methods are no longer tenable. Our methods rely on stochastic approximations, which are computationally efficient as they maintain one iterate as a parameter estimate, and successively update that iterate based on a single data point. When the update is based on a noisy gradient, the stochastic approximation is known as standard stochastic gradient descent, which has been fundamental in modern applications with large data sets. Additionally, our methods are numerically stable because they employ implicit updates of the iterates. Intuitively, an implicit update is a shrinked version of a standard one, where the shrinkage factor depends on the observed Fisher information at the corresponding data point. This shrinkage prevents numerical divergence of the iterates, which can be caused either by excess noise or outliers. Our sgd package in R offers the most extensive and robust implementation of stochastic gradient descent methods. We demonstrate that sgd dominates alternative software in runtime for several estimation problems with massive data sets. Our applications include the wide class of generalized linear models as well as M-estimation for robust regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge