Si Kai Lee
Robust Inference for High-Dimensional Linear Models via Residual Randomization
Jun 14, 2021

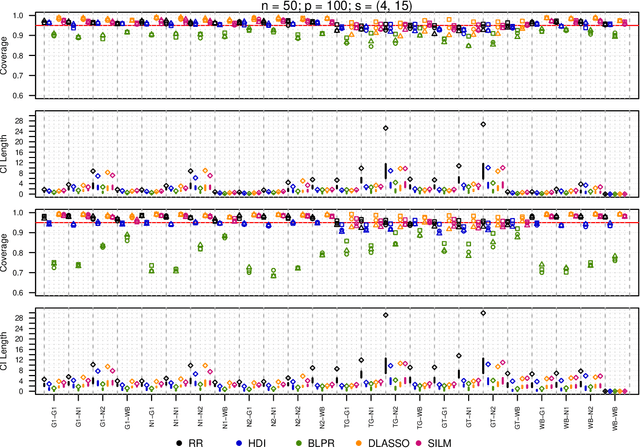
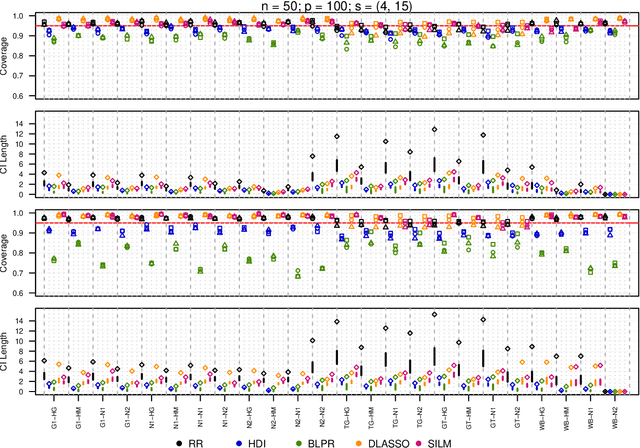
Abstract:We propose a residual randomization procedure designed for robust Lasso-based inference in the high-dimensional setting. Compared to earlier work that focuses on sub-Gaussian errors, the proposed procedure is designed to work robustly in settings that also include heavy-tailed covariates and errors. Moreover, our procedure can be valid under clustered errors, which is important in practice, but has been largely overlooked by earlier work. Through extensive simulations, we illustrate our method's wider range of applicability as suggested by theory. In particular, we show that our method outperforms state-of-art methods in challenging, yet more realistic, settings where the distribution of covariates is heavy-tailed or the sample size is small, while it remains competitive in standard, ``well behaved" settings previously studied in the literature.
Dual IV: A Single Stage Instrumental Variable Regression
Oct 27, 2019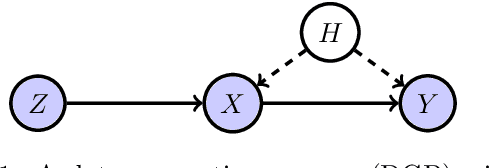
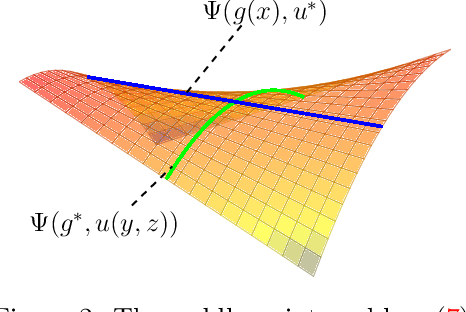
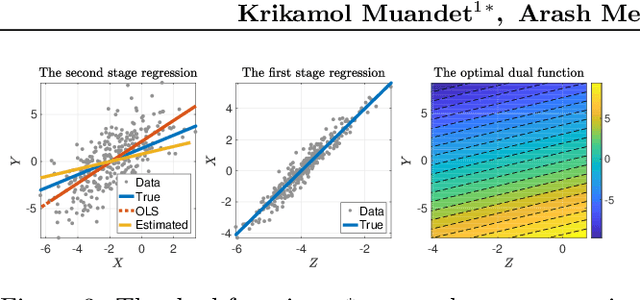

Abstract:We present a novel single-stage procedure for instrumental variable (IV) regression called DualIV which simplifies traditional two-stage regression via a dual formulation. We show that the common two-stage procedure can alternatively be solved via generalized least squares. Our formulation circumvents the first-stage regression which can be a bottleneck in modern two-stage procedures for IV regression. We also show that our framework is closely related to the generalized method of moments (GMM) with specific assumptions. This highlights the fundamental connection between GMM and two-stage procedures in IV literature. Using the proposed framework, we develop a simple kernel-based algorithm with consistency guarantees. Lastly, we give empirical results illustrating the advantages of our method over the existing two-stage algorithms.
Private Causal Inference using Propensity Scores
May 29, 2019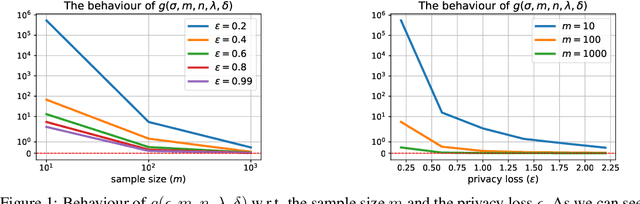

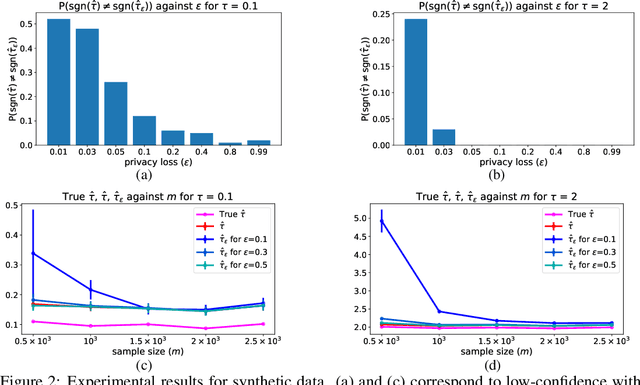
Abstract:The use of propensity score methods to reduce selection bias when determining causal effects is common practice for observational studies. Although such studies in econometrics, social science, and medicine often rely on sensitive data, there has been no prior work on privatising the propensity scores used to ascertain causal effects from observed data. In this paper, we demonstrate how to privatise the propensity score and quantify how the added noise for privatisation affects the propensity score as well as subsequent causal inference. We test our methods on both simulated and real-world datasets. The results are consistent with our theoretical findings that the privatisation preserves the validity of subsequent causal analysis with high probability. More importantly, our results empirically demonstrate that the proposed solutions are practical for moderately-sized datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge