Dual IV: A Single Stage Instrumental Variable Regression

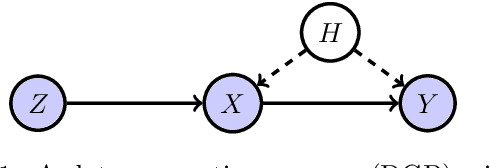
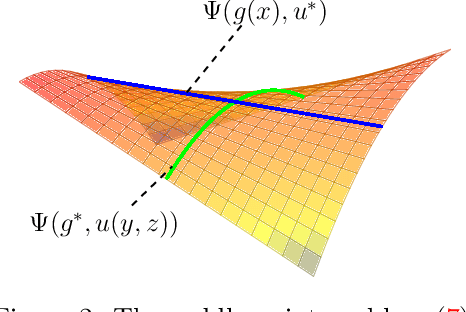
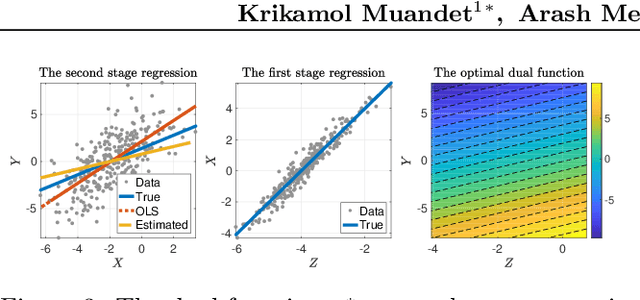
We present a novel single-stage procedure for instrumental variable (IV) regression called DualIV which simplifies traditional two-stage regression via a dual formulation. We show that the common two-stage procedure can alternatively be solved via generalized least squares. Our formulation circumvents the first-stage regression which can be a bottleneck in modern two-stage procedures for IV regression. We also show that our framework is closely related to the generalized method of moments (GMM) with specific assumptions. This highlights the fundamental connection between GMM and two-stage procedures in IV literature. Using the proposed framework, we develop a simple kernel-based algorithm with consistency guarantees. Lastly, we give empirical results illustrating the advantages of our method over the existing two-stage algorithms.