Robust Inference for High-Dimensional Linear Models via Residual Randomization

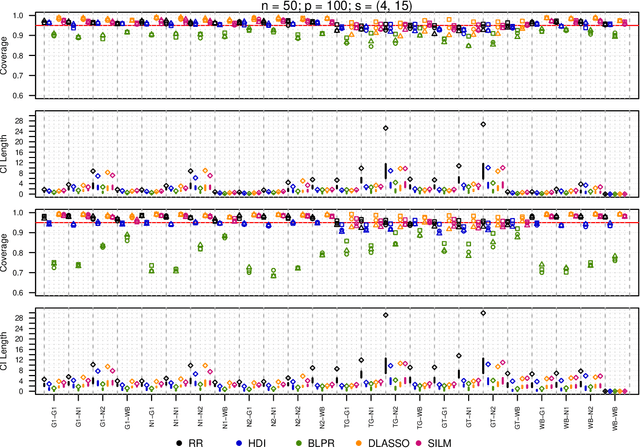
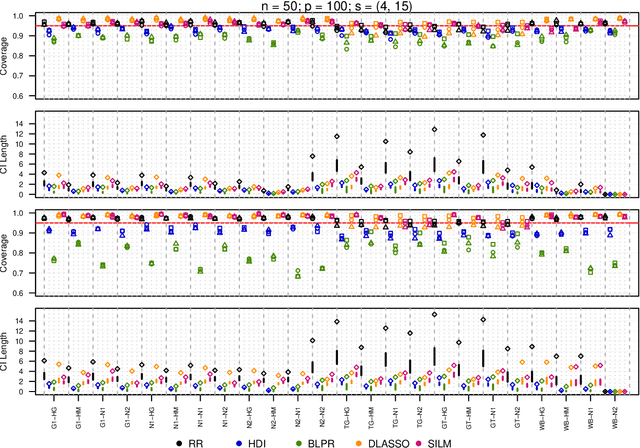
We propose a residual randomization procedure designed for robust Lasso-based inference in the high-dimensional setting. Compared to earlier work that focuses on sub-Gaussian errors, the proposed procedure is designed to work robustly in settings that also include heavy-tailed covariates and errors. Moreover, our procedure can be valid under clustered errors, which is important in practice, but has been largely overlooked by earlier work. Through extensive simulations, we illustrate our method's wider range of applicability as suggested by theory. In particular, we show that our method outperforms state-of-art methods in challenging, yet more realistic, settings where the distribution of covariates is heavy-tailed or the sample size is small, while it remains competitive in standard, ``well behaved" settings previously studied in the literature.

High-dimensional Functional Graphical Model Structure Learning via Neighborhood Selection Approach

Undirected graphical models have been widely used to model the conditional independence structure of high-dimensional random vector data for years. In many modern applications such as EEG and fMRI data, the observations are multivariate random functions rather than scalars. To model the conditional independence of this type of data, functional graphical models are proposed and have attracted an increasing attention in recent years. In this paper, we propose a neighborhood selection approach to estimate Gaussian functional graphical models. We first estimate the neighborhood of all nodes via function-on-function regression, and then we can recover the whole graph structure based on the neighborhood information. By estimating conditional structure directly, we can circumvent the need of a well-defined precision operator which generally does not exist. Besides, we can better explore the effect of the choice of function basis for dimension reduction. We give a criterion for choosing the best function basis and motivate two practically useful choices, which we justified by both theory and experiments and show that they are better than expanding each function onto its own FPCA basis as in previous literature. In addition, the neighborhood selection approach is computationally more efficient than fglasso as it is more easy to do parallel computing. The statistical consistency of our proposed methods in high-dimensional setting are supported by both theory and experiment.

FuDGE: Functional Differential Graph Estimation with fully and discretely observed curves

We consider the problem of estimating the difference between two functional undirected graphical models with shared structures. In many applications, data are naturally regarded as high-dimensional random function vectors rather than multivariate scalars. For example, electroencephalography (EEG) data are more appropriately treated as functions of time. In these problems, not only can the number of functions measured per sample be large, but each function is itself an infinite dimensional object, making estimation of model parameters challenging. In practice, curves are usually discretely observed, which makes graph structure recovery even more challenging. We formally characterize when two functional graphical models are comparable and propose a method that directly estimates the functional differential graph, which we term FuDGE. FuDGE avoids separate estimation of each graph, which allows for estimation in problems where individual graphs are dense, but their difference is sparse. We show that FuDGE consistently estimates the functional differential graph in a high-dimensional setting for both discretely observed and fully observed function paths. We illustrate finite sample properties of our method through simulation studies. In order to demonstrate the benefits of our method, we propose Joint Functional Graphical Lasso as a competitor, which is a generalization of the Joint Graphical Lasso. Finally, we apply our method to EEG data to uncover differences in functional brain connectivity between alcoholics and control subjects.

Direct Estimation of Differential Functional Graphical Models

We consider the problem of estimating the difference between two functional undirected graphical models with shared structures. In many applications, data are naturally regarded as high-dimensional random function vectors rather than multivariate scalars. For example, electroencephalography (EEG) data are more appropriately treated as functions of time. In these problems, not only can the number of functions measured per sample be large, but each function is itself an infinite dimensional object, making estimation of model parameters challenging. We develop a method that directly estimates the difference of graphs, avoiding separate estimation of each graph, and show it is consistent in certain high-dimensional settings. We illustrate finite sample properties of our method through simulation studies. Finally, we apply our method to EEG data to uncover differences in functional brain connectivity between alcoholics and control subjects.

On the use of bootstrap with variational inference: Theory, interpretation, and a two-sample test example

Variational inference is a general approach for approximating complex density functions, such as those arising in latent variable models, popular in machine learning. It has been applied to approximate the maximum likelihood estimator and to carry out Bayesian inference, however, quantification of uncertainty with variational inference remains challenging from both theoretical and practical perspectives. This paper is concerned with developing uncertainty measures for variational inference by using bootstrap procedures. We first develop two general bootstrap approaches for assessing the uncertainty of a variational estimate and the study the underlying bootstrap theory in both fixed- and increasing-dimension settings. We then use the bootstrap approach and our theoretical results in the context of mixed membership modeling with multivariate binary data on functional disability from the National Long Term Care Survey. We carry out a two-sample approach to test for changes in the repeated measures of functional disability for the subset of individuals present in 1989 and 1994 waves.