Yen-Chi Chen
Department of Statistics, University of Washington, Seattle
Markov Missing Graph: A Graphical Approach for Missing Data Imputation
Sep 03, 2025Abstract:We introduce the Markov missing graph (MMG), a novel framework that imputes missing data based on undirected graphs. MMG leverages conditional independence relationships to locally decompose the imputation model. To establish the identification, we introduce the Principle of Available Information (PAI), which guides the use of all relevant observed data. We then propose a flexible statistical learning paradigm, MMG Imputation Risk Minimization under PAI, that frames the imputation task as an empirical risk minimization problem. This framework is adaptable to various modeling choices. We develop theories of MMG, including the connection between MMG and Little's complete-case missing value assumption, recovery under missing completely at random, efficiency theory, and graph-related properties. We show the validity of our method with simulation studies and illustrate its application with a real-world Alzheimer's data set.
Doubly Robust Inference on Causal Derivative Effects for Continuous Treatments
Jan 12, 2025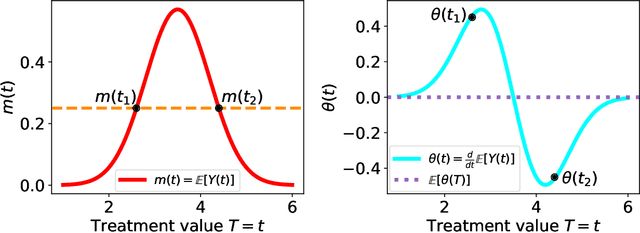
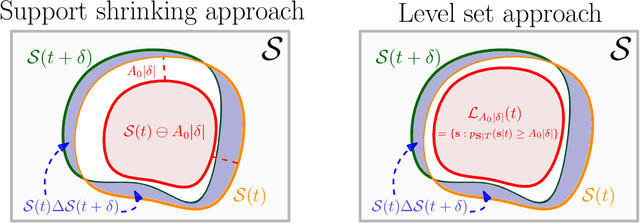
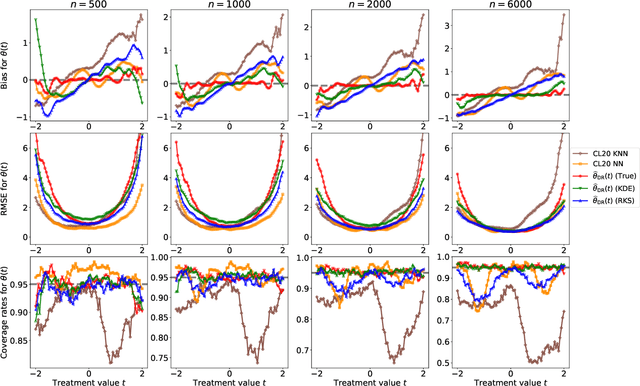
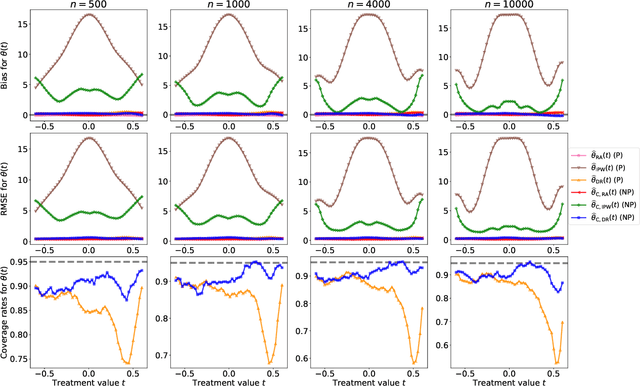
Abstract:Statistical methods for causal inference with continuous treatments mainly focus on estimating the mean potential outcome function, commonly known as the dose-response curve. However, it is often not the dose-response curve but its derivative function that signals the treatment effect. In this paper, we investigate nonparametric inference on the derivative of the dose-response curve with and without the positivity condition. Under the positivity and other regularity conditions, we propose a doubly robust (DR) inference method for estimating the derivative of the dose-response curve using kernel smoothing. When the positivity condition is violated, we demonstrate the inconsistency of conventional inverse probability weighting (IPW) and DR estimators, and introduce novel bias-corrected IPW and DR estimators. In all settings, our DR estimator achieves asymptotic normality at the standard nonparametric rate of convergence. Additionally, our approach reveals an interesting connection to nonparametric support and level set estimation problems. Finally, we demonstrate the applicability of our proposed estimators through simulations and a case study of evaluating a job training program.
Residual Scheduling: A New Reinforcement Learning Approach to Solving Job Shop Scheduling Problem
Oct 03, 2023Abstract:Job-shop scheduling problem (JSP) is a mathematical optimization problem widely used in industries like manufacturing, and flexible JSP (FJSP) is also a common variant. Since they are NP-hard, it is intractable to find the optimal solution for all cases within reasonable times. Thus, it becomes important to develop efficient heuristics to solve JSP/FJSP. A kind of method of solving scheduling problems is construction heuristics, which constructs scheduling solutions via heuristics. Recently, many methods for construction heuristics leverage deep reinforcement learning (DRL) with graph neural networks (GNN). In this paper, we propose a new approach, named residual scheduling, to solving JSP/FJSP. In this new approach, we remove irrelevant machines and jobs such as those finished, such that the states include the remaining (or relevant) machines and jobs only. Our experiments show that our approach reaches state-of-the-art (SOTA) among all known construction heuristics on most well-known open JSP and FJSP benchmarks. In addition, we also observe that even though our model is trained for scheduling problems of smaller sizes, our method still performs well for scheduling problems of large sizes. Interestingly in our experiments, our approach even reaches zero gap for 49 among 50 JSP instances whose job numbers are more than 150 on 20 machines.
Skeleton Regression: A Graph-Based Approach to Estimation with Manifold Structure
Mar 19, 2023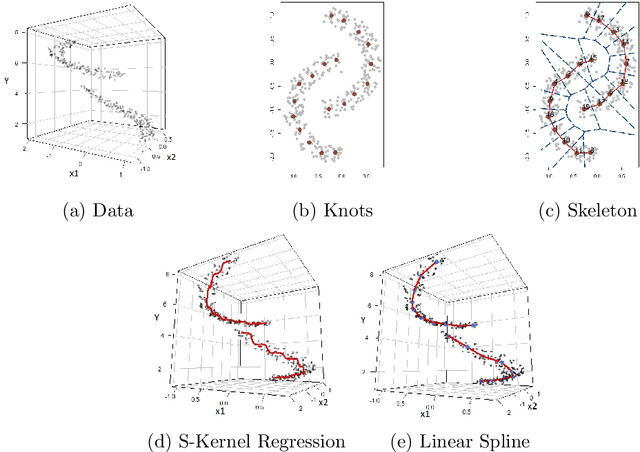

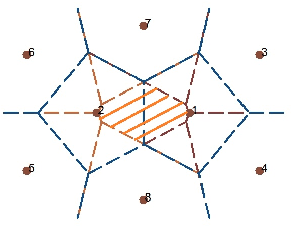

Abstract:We introduce a new regression framework designed to deal with large-scale, complex data that lies around a low-dimensional manifold. Our approach first constructs a graph representation, referred to as the skeleton, to capture the underlying geometric structure. We then define metrics on the skeleton graph and apply nonparametric regression techniques, along with feature transformations based on the graph, to estimate the regression function. In addition to the included nonparametric methods, we also discuss the limitations of some nonparametric regressors with respect to the general metric space such as the skeleton graph. The proposed regression framework allows us to bypass the curse of dimensionality and provides additional advantages that it can handle the union of multiple manifolds and is robust to additive noise and noisy observations. We provide statistical guarantees for the proposed method and demonstrate its effectiveness through simulations and real data examples.
Mode and Ridge Estimation in Euclidean and Directional Product Spaces: A Mean Shift Approach
Oct 16, 2021
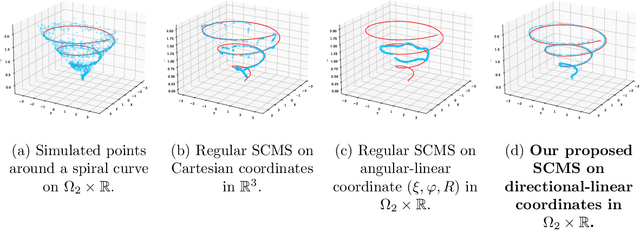
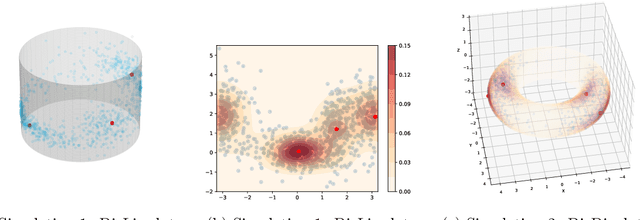

Abstract:The set of local modes and the ridge lines estimated from a dataset are important summary characteristics of the data-generating distribution. In this work, we consider estimating the local modes and ridges from point cloud data in a product space with two or more Euclidean/directional metric spaces. Specifically, we generalize the well-known (subspace constrained) mean shift algorithm to the product space setting and illuminate some pitfalls in such generalization. We derive the algorithmic convergence of the proposed method, provide practical guidelines on the implementation, and demonstrate its effectiveness on both simulated and real datasets.
Linear Convergence of the Subspace Constrained Mean Shift Algorithm: From Euclidean to Directional Data
Apr 29, 2021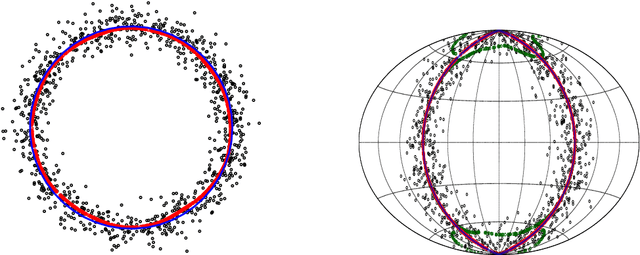

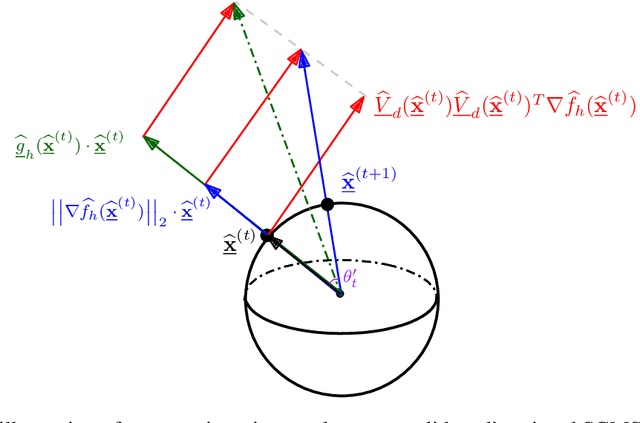
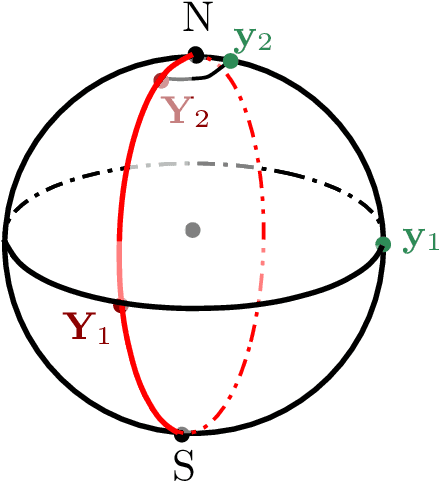
Abstract:This paper studies linear convergence of the subspace constrained mean shift (SCMS) algorithm, a well-known algorithm for identifying a density ridge defined by a kernel density estimator. By arguing that the SCMS algorithm is a special variant of a subspace constrained gradient ascent (SCGA) algorithm with an adaptive step size, we derive linear convergence of such SCGA algorithm. While the existing research focuses mainly on density ridges in the Euclidean space, we generalize density ridges and the SCMS algorithm to directional data. In particular, we establish the stability theorem of density ridges with directional data and prove the linear convergence of our proposed directional SCMS algorithm.
Skeleton Clustering: Dimension-Free Density-based Clustering
Apr 21, 2021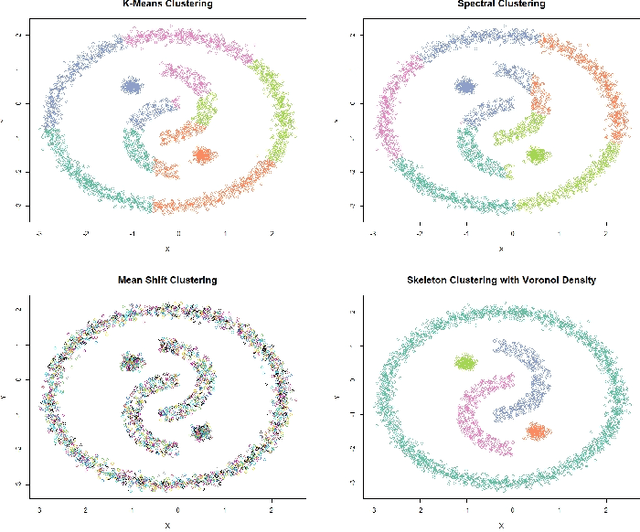

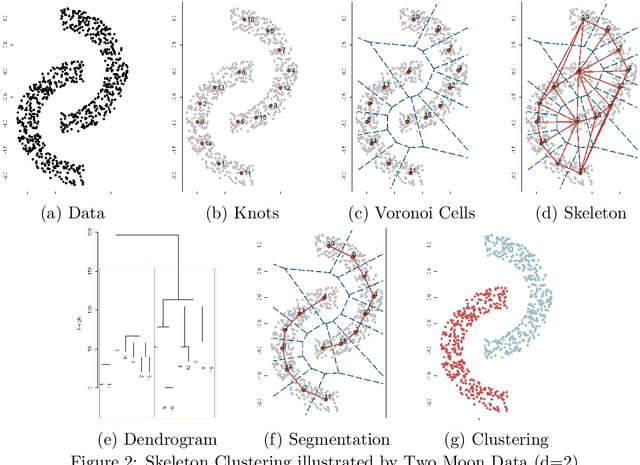
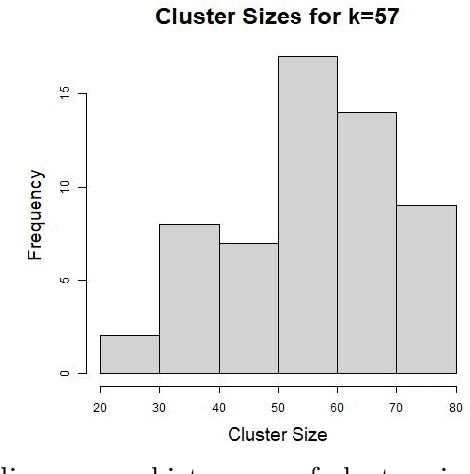
Abstract:We introduce a density-based clustering method called skeleton clustering that can detect clusters in multivariate and even high-dimensional data with irregular shapes. To bypass the curse of dimensionality, we propose surrogate density measures that are less dependent on the dimension but have intuitive geometric interpretations. The clustering framework constructs a concise representation of the given data as an intermediate step and can be thought of as a combination of prototype methods, density-based clustering, and hierarchical clustering. We show by theoretical analysis and empirical studies that the skeleton clustering leads to reliable clusters in multivariate and high-dimensional scenarios.
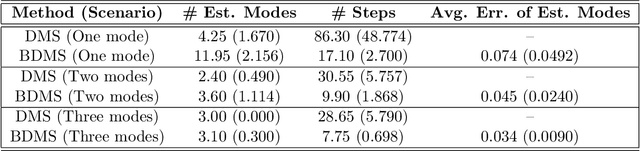
The EM Perspective of Directional Mean Shift Algorithm
Jan 25, 2021
Abstract:The directional mean shift (DMS) algorithm is a nonparametric method for pursuing local modes of densities defined by kernel density estimators on the unit hypersphere. In this paper, we show that any DMS iteration can be viewed as a generalized Expectation-Maximization (EM) algorithm; in particular, when the von Mises kernel is applied, it becomes an exact EM algorithm. Under the (generalized) EM framework, we provide a new proof for the ascending property of density estimates and demonstrate the global convergence of directional mean shift sequences. Finally, we give a new insight into the linear convergence of the DMS algorithm.
Kernel Smoothing, Mean Shift, and Their Learning Theory with Directional Data
Oct 23, 2020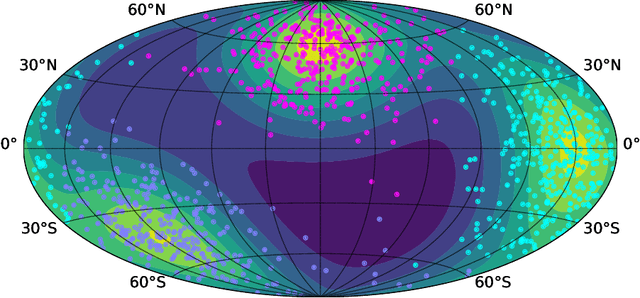
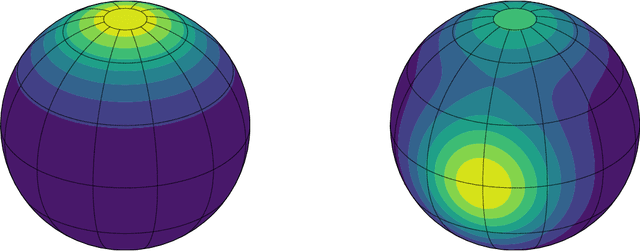
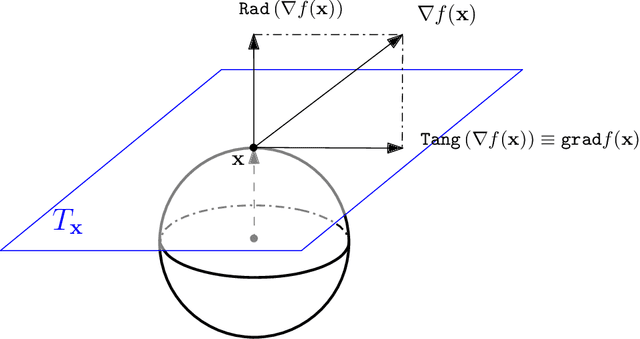
Abstract:Directional data consist of observations distributed on a (hyper)sphere, and appear in many applied fields, such as astronomy, ecology, and environmental science. This paper studies both statistical and computational problems of kernel smoothing for directional data. We generalize the classical mean shift algorithm to directional data, which allows us to identify local modes of the directional kernel density estimator (KDE). The statistical convergence rates of the directional KDE and its derivatives are derived, and the problem of mode estimation is examined. We also prove the ascending property of our directional mean shift algorithm and investigate a general problem of gradient ascent on the unit hypersphere. To demonstrate the applicability of our proposed algorithm, we evaluate it as a mode clustering method on both simulated and real-world datasets.
Polygames: Improved Zero Learning
Jan 27, 2020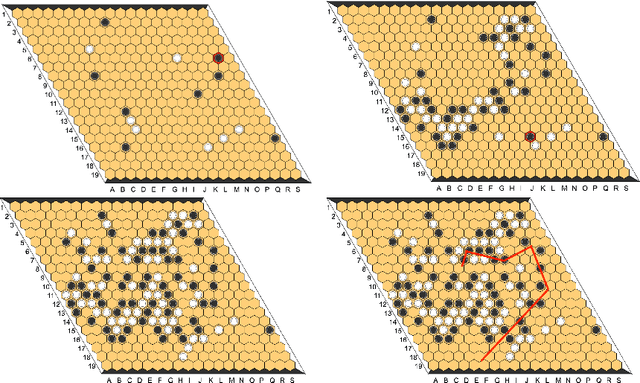
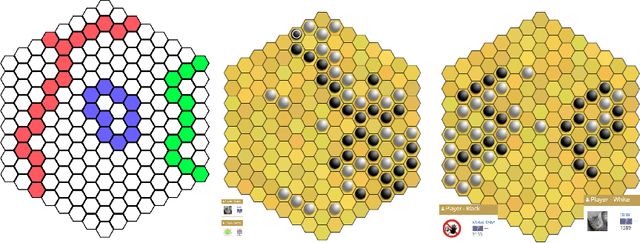
Abstract:Since DeepMind's AlphaZero, Zero learning quickly became the state-of-the-art method for many board games. It can be improved using a fully convolutional structure (no fully connected layer). Using such an architecture plus global pooling, we can create bots independent of the board size. The training can be made more robust by keeping track of the best checkpoints during the training and by training against them. Using these features, we release Polygames, our framework for Zero learning, with its library of games and its checkpoints. We won against strong humans at the game of Hex in 19x19, which was often said to be untractable for zero learning; and in Havannah. We also won several first places at the TAAI competitions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge