Mode and Ridge Estimation in Euclidean and Directional Product Spaces: A Mean Shift Approach
Paper and Code
Oct 16, 2021
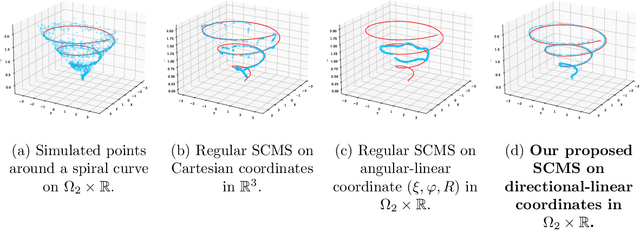
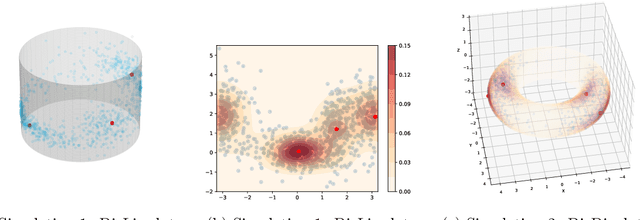

The set of local modes and the ridge lines estimated from a dataset are important summary characteristics of the data-generating distribution. In this work, we consider estimating the local modes and ridges from point cloud data in a product space with two or more Euclidean/directional metric spaces. Specifically, we generalize the well-known (subspace constrained) mean shift algorithm to the product space setting and illuminate some pitfalls in such generalization. We derive the algorithmic convergence of the proposed method, provide practical guidelines on the implementation, and demonstrate its effectiveness on both simulated and real datasets.
* 51 pages, 10 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge