Doubly Robust Inference on Causal Derivative Effects for Continuous Treatments
Paper and Code
Jan 12, 2025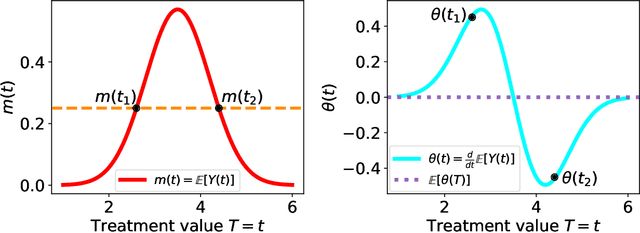
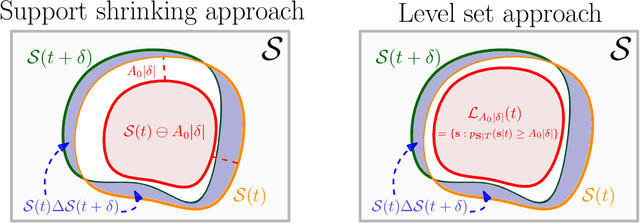
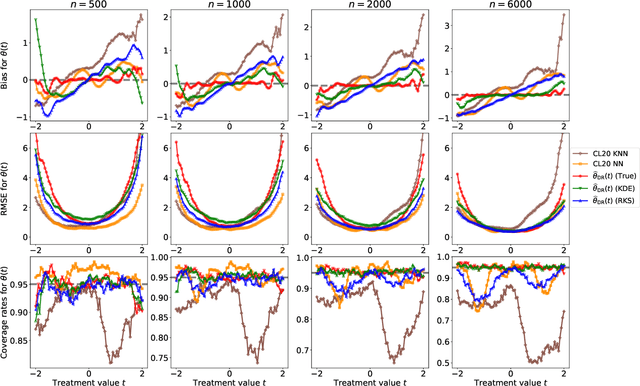
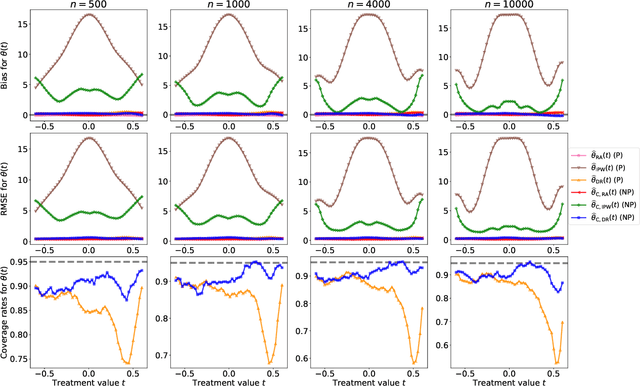
Statistical methods for causal inference with continuous treatments mainly focus on estimating the mean potential outcome function, commonly known as the dose-response curve. However, it is often not the dose-response curve but its derivative function that signals the treatment effect. In this paper, we investigate nonparametric inference on the derivative of the dose-response curve with and without the positivity condition. Under the positivity and other regularity conditions, we propose a doubly robust (DR) inference method for estimating the derivative of the dose-response curve using kernel smoothing. When the positivity condition is violated, we demonstrate the inconsistency of conventional inverse probability weighting (IPW) and DR estimators, and introduce novel bias-corrected IPW and DR estimators. In all settings, our DR estimator achieves asymptotic normality at the standard nonparametric rate of convergence. Additionally, our approach reveals an interesting connection to nonparametric support and level set estimation problems. Finally, we demonstrate the applicability of our proposed estimators through simulations and a case study of evaluating a job training program.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge