Scalable Policy Maximization Under Network Interference

Many interventions, such as vaccines in clinical trials or coupons in online marketplaces, must be assigned sequentially without full knowledge of their effects. Multi-armed bandit algorithms have proven successful in such settings. However, standard independence assumptions fail when the treatment status of one individual impacts the outcomes of others, a phenomenon known as interference. We study optimal-policy learning under interference on a dynamic network. Existing approaches to this problem require repeated observations of the same fixed network and struggle to scale in sample size beyond as few as fifteen connected units -- both limit applications. We show that under common assumptions on the structure of interference, rewards become linear. This enables us to develop a scalable Thompson sampling algorithm that maximizes policy impact when a new $n$-node network is observed each round. We prove a Bayesian regret bound that is sublinear in $n$ and the number of rounds. Simulation experiments show that our algorithm learns quickly and outperforms existing methods. The results close a key scalability gap between causal inference methods for interference and practical bandit algorithms, enabling policy optimization in large-scale networked systems.

Stabilizing Temporal Difference Learning via Implicit Stochastic Approximation

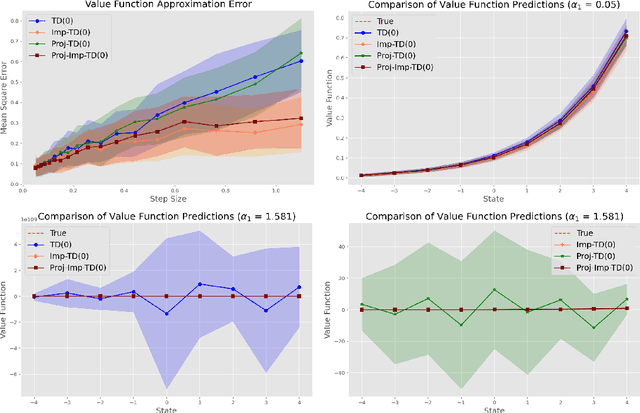
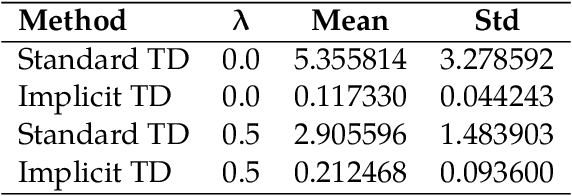
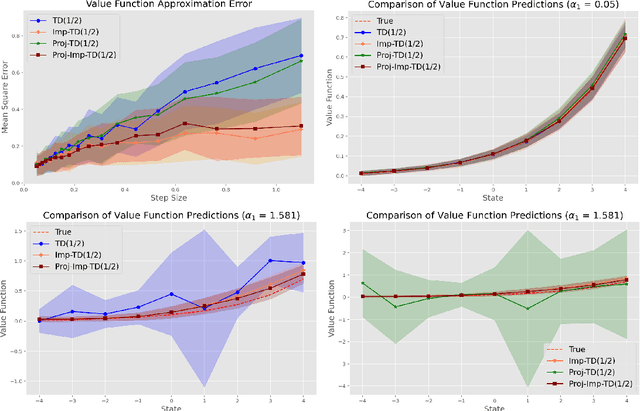
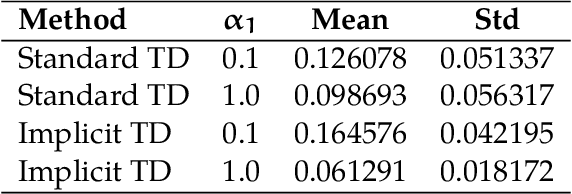
Temporal Difference (TD) learning is a foundational algorithm in reinforcement learning (RL). For nearly forty years, TD learning has served as a workhorse for applied RL as well as a building block for more complex and specialized algorithms. However, despite its widespread use, it is not without drawbacks, the most prominent being its sensitivity to step size. A poor choice of step size can dramatically inflate the error of value estimates and slow convergence. Consequently, in practice, researchers must use trial and error in order to identify a suitable step size -- a process that can be tedious and time consuming. As an alternative, we propose implicit TD algorithms that reformulate TD updates into fixed-point equations. These updates are more stable and less sensitive to step size without sacrificing computational efficiency. Moreover, our theoretical analysis establishes asymptotic convergence guarantees and finite-time error bounds. Our results demonstrate their robustness and practicality for modern RL tasks, establishing implicit TD as a versatile tool for policy evaluation and value approximation.

Exploiting Concavity Information in Gaussian Process Contextual Bandit Optimization

The contextual bandit framework is widely used to solve sequential optimization problems where the reward of each decision depends on auxiliary context variables. In settings such as medicine, business, and engineering, the decision maker often possesses additional structural information on the generative model that can potentially be used to improve the efficiency of bandit algorithms. We consider settings in which the mean reward is known to be a concave function of the action for each fixed context. Examples include patient-specific dose-response curves in medicine and expected profit in online advertising auctions. We propose a contextual bandit algorithm that accelerates optimization by conditioning the posterior of a Bayesian Gaussian Process model on this concavity information. We design a novel shape-constrained reward function estimator using a specially chosen regression spline basis and constrained Gaussian Process posterior. Using this model, we propose a UCB algorithm and derive corresponding regret bounds. We evaluate our algorithm on numerical examples and test functions used to study optimal dosing of Anti-Clotting medication.

Empirical Bound Information-Directed Sampling for Norm-Agnostic Bandits

Information-directed sampling (IDS) is a powerful framework for solving bandit problems which has shown strong results in both Bayesian and frequentist settings. However, frequentist IDS, like many other bandit algorithms, requires that one have prior knowledge of a (relatively) tight upper bound on the norm of the true parameter vector governing the reward model in order to achieve good performance. Unfortunately, this requirement is rarely satisfied in practice. As we demonstrate, using a poorly calibrated bound can lead to significant regret accumulation. To address this issue, we introduce a novel frequentist IDS algorithm that iteratively refines a high-probability upper bound on the true parameter norm using accumulating data. We focus on the linear bandit setting with heteroskedastic subgaussian noise. Our method leverages a mixture of relevant information gain criteria to balance exploration aimed at tightening the estimated parameter norm bound and directly searching for the optimal action. We establish regret bounds for our algorithm that do not depend on an initially assumed parameter norm bound and demonstrate that our method outperforms state-of-the-art IDS and UCB algorithms.

Sex Trafficking Detection with Ordinal Regression Neural Networks

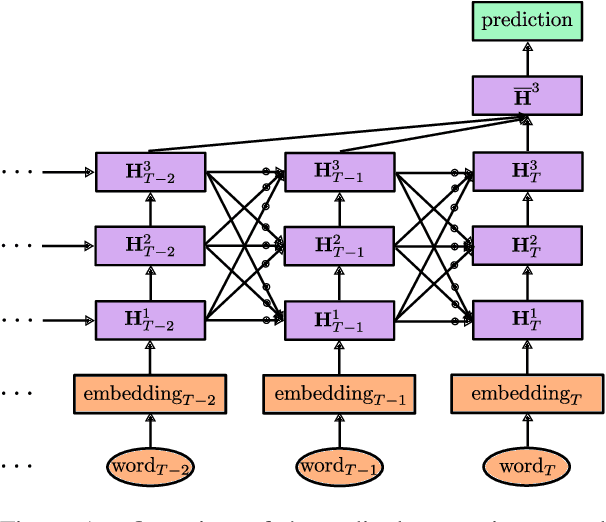
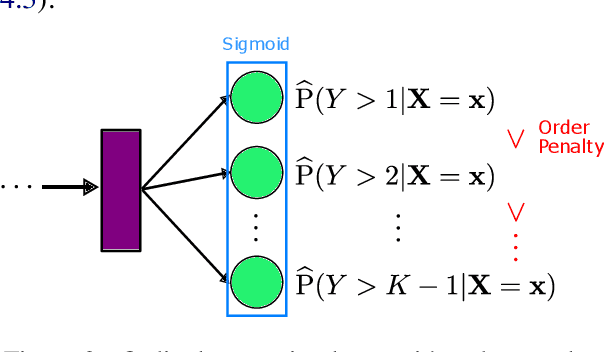
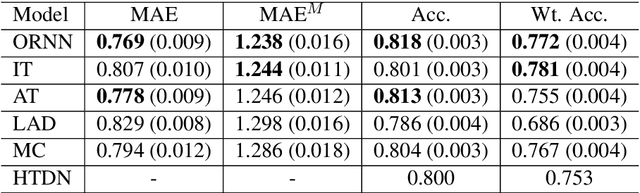
Sex trafficking is a global epidemic. Escort websites are a primary vehicle for selling the services of such trafficking victims and thus a major driver of trafficker revenue. Many law enforcement agencies do not have the resources to manually identify leads from the millions of escort ads posted across dozens of public websites. We propose an ordinal regression neural network to identify escort ads that are likely linked to sex trafficking. Our model uses a modified cost function to mitigate inconsistencies in predictions often associated with nonparametric ordinal regression and leverages recent advancements in deep learning to improve prediction accuracy. The proposed method significantly improves on the previous state-of-the-art on Trafficking-10K, an expert-annotated dataset of escort ads. Additionally, because traffickers use acronyms, deliberate typographical errors, and emojis to replace explicit keywords, we demonstrate how to expand the lexicon of trafficking flags through word embeddings and t-SNE.

Convergence Rates of Posterior Distributions in Markov Decision Process

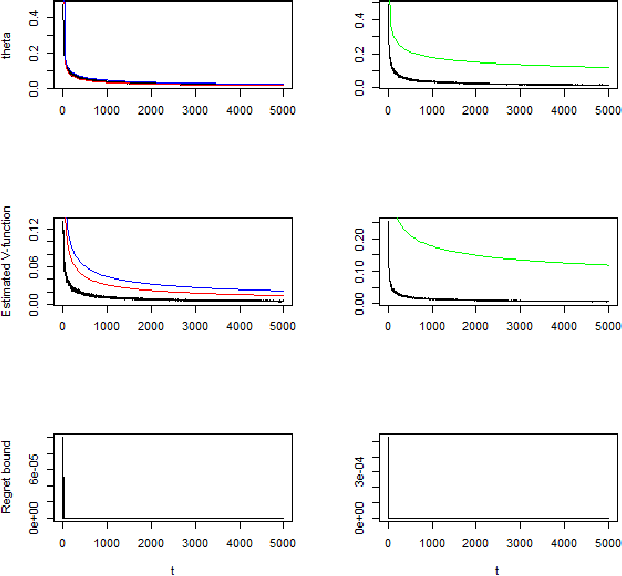
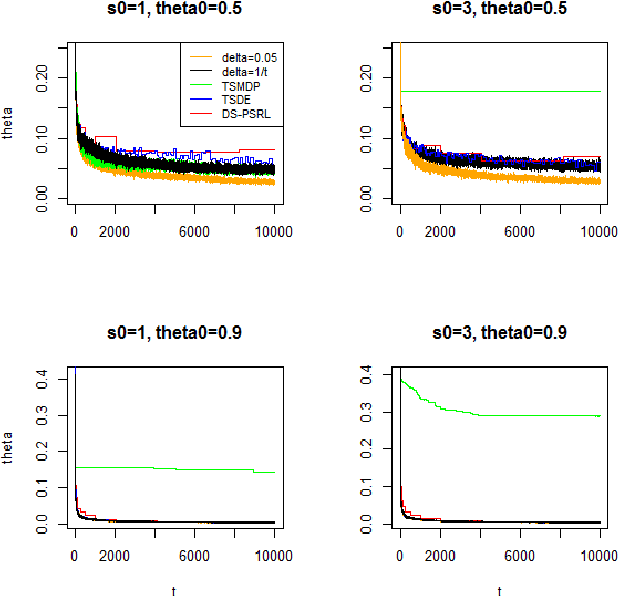
In this paper, we show the convergence rates of posterior distributions of the model dynamics in a MDP for both episodic and continuous tasks. The theoretical results hold for general state and action space and the parameter space of the dynamics can be infinite dimensional. Moreover, we show the convergence rates of posterior distributions of the mean accumulative reward under a fixed or the optimal policy and of the regret bound. A variant of Thompson sampling algorithm is proposed which provides both posterior convergence rates for the dynamics and the regret-type bound. Then the previous results are extended to Markov games. Finally, we show numerical results with three simulation scenarios and conclude with discussions.

Parameterized Exploration

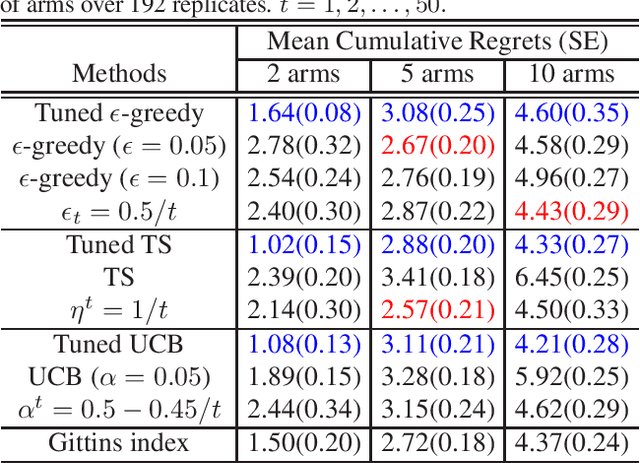
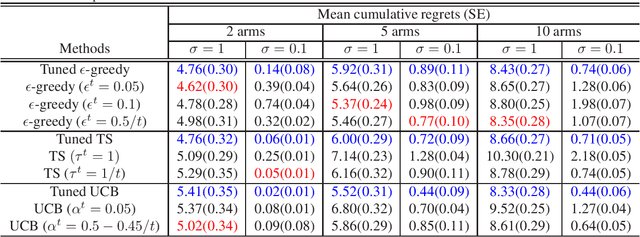
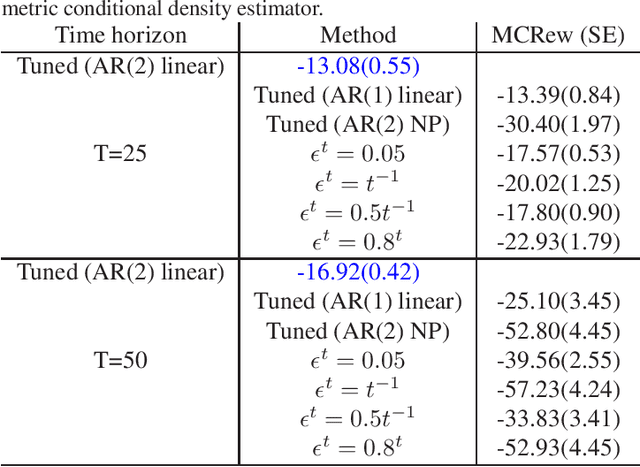
We introduce Parameterized Exploration (PE), a simple family of methods for model-based tuning of the exploration schedule in sequential decision problems. Unlike common heuristics for exploration, our method accounts for the time horizon of the decision problem as well as the agent's current state of knowledge of the dynamics of the decision problem. We show our method as applied to several common exploration techniques has superior performance relative to un-tuned counterparts in Bernoulli and Gaussian multi-armed bandits, contextual bandits, and a Markov decision process based on a mobile health (mHealth) study. We also examine the effects of the accuracy of the estimated dynamics model on the performance of PE.