Convergence Rates of Posterior Distributions in Markov Decision Process
Paper and Code
Jul 22, 2019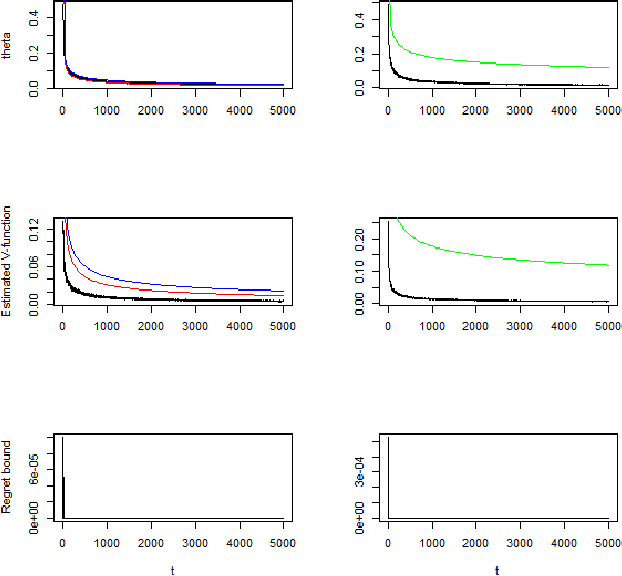

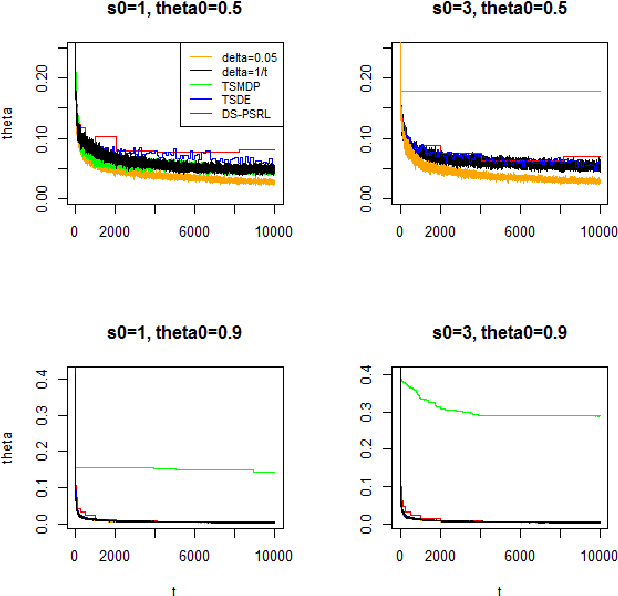

In this paper, we show the convergence rates of posterior distributions of the model dynamics in a MDP for both episodic and continuous tasks. The theoretical results hold for general state and action space and the parameter space of the dynamics can be infinite dimensional. Moreover, we show the convergence rates of posterior distributions of the mean accumulative reward under a fixed or the optimal policy and of the regret bound. A variant of Thompson sampling algorithm is proposed which provides both posterior convergence rates for the dynamics and the regret-type bound. Then the previous results are extended to Markov games. Finally, we show numerical results with three simulation scenarios and conclude with discussions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge